单因素方差分析

7．1．1 解决的问题

方差分析可用于判断多项政策的效果、多个群体的人对某一问题的评价、多组人员的工资水平、多种训练方法的效果、多种药品的效果、多种生产技术的效果、多台设备的故障率、多个品牌或多种促销方式的销售效果、多个土壤条件或肥料品种对农作物产量的影响等是否有显著区别。为更好地理解单因素方差分析的含义，先通过一个例子来说明方差分析的相关概念及方差分析所要解决的问题。

【例7‐1】 消费者与产品生产者、销售者或服务提供商之间经常发生纠纷。纠纷发生后，消费者往往会向消费者组织投诉。为了对几个行业的服务质量进行评价，消费者组织在零售业、旅游业、航空公司、家电制造业分别抽取了不同的企业作为样本，统计了消费者的投诉次数，如表7‐1所示。每个行业中所抽取的企业，假定在服务对象、服务内容、企业规模等方面是基本相同的。一般而言，受到的投诉次数越多，服务质量越差。消费者组织希望知道这几个行业之间的服务质量是否有显著差异。

表7‐1 消费者对四个行业的投诉次数

资料来源：贾俊平，何晓群，金勇进．统计学（第四版）．北京：中国人民大学出版社，2009．

在方差分析中，所要检验的对象称为因素（factor），因素的不同表现是水平（level）或处理（treatment），每个因素水平下得到的样本数据称为观测值。在上例中，行业就是要检验的对象，即因素。零售业、旅游业、航空公司、家电制造业是因子的四个取值，称为水平或处理。在每个行业下得到的样本数据（投诉次数）称为观察值。本例的单因素方差分析研究的问题是分类变量对数值型因变量的影响，即分析行业对投诉次数的影响。

7．1．2 分析原理

7．1．2．1 误差分解

在上例中，我们首先注意到，同一行业中企业的投诉次数是不同的。由于样本是随机抽取的，因此它们之间的差异可以看成是随机因素造成的，或者说是抽样的随机性造成了随机误差。这种来自样本内部的数据误差成为组内误差（within groups），它反映了样本数据自身的离散程度。其次，不同行业内企业的投诉次数也是不同的。这种来自样本之间的数据误差称为组间误差（between groups），组间误差可能是抽样造成的随机误差，也可能是行业造成的系统误差引起，它反映了不同样本之间数据的离散程度。

在统计中，数据的误差通常用平方和（sum of squares）来表示。全部数据误差大小的平方和称为总平方和（sum of squares for total），记为SST，它反映了全部观察值的离散状况。反映组内误差大小的平方和称为组内平方和，或残差平方和（sum of squares for error），记为SS组内。反映组间误差大小的平方和称为组间平方和（sum of squares for factor），记为SS组间。可以证明，总平方和为组间平方和与组内平方和之和，即SST＝SS组间＋SS组内。

7．1．2．2 误差分析

由于误差平方和的大小与观察值的数量有关，为消除观察值数量对误差平方和大小的影响，需要用平方和除以对应的自由度，得到均方（mean square），也称方差（variance）。组间平方和除以自由度得到组间方差（between groups variance）或因子均方，组内平方和除以自由度得到组内方差（within groups variance）或残差均方。

如果行业对投诉次数没有影响，组间误差只包含随机误差，没有系统误差。这时，组间方差与组内方差就应该很接近。如果行业对投诉次数有影响，组间误差除了包含系统误差外，还包含了系统误差，这时组间方差就会大于组内方差，它们之间的比值就会大于1。当这个比值超过一定水平时，就可以认为行业对投诉次数有显著影响。

7．1．2．3 统计决策

首先提出假设。设零售业、旅游业、航空公司和家电制造业投诉次数的均值分别为μ1、μ2、μ3和μ4。为检验行业对投诉次数是否有显著影响，提出如下假设：

H0：μ1＝ μ2＝ μ3＝ μ4

H1：μ1、μ2、μ3、μ4不全相等

然后计算检验统计量：

F＝～Fk－1，n－k

根据给定的显著性水平α，若显著性概率P＜ α，则拒绝原假设H0，行业对投诉次数有显著影响。若P＞ α，则不拒绝原假设H0，不能认为行业对投诉次数有显著影响。

7．1．2．4 关系强度判断

由各误差平方和的含义可知，组间平方和度量了自变量（行业）对因变量（投诉次数）的影响效应。组间平方和在总平方和中占据的比例称为判断系数R2，R2越大，分类自变量与数值型因变量的关系就越强。

R2＝

单因素方差分析的计算过程：

（1）总平方和SST＝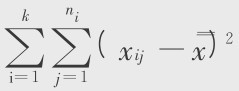

（2）组间平方和SS组间＝＝1 ＝1 2

（3）残差平方和SS残差＝2

（4）组间方差MS组间＝

（5）残差方差MS残差＝

（6）检验统计量F＝

知识链接

方差分析需要满足的三个基本假设

（1）正态性（normality）。每种处理所对应的总体都应服从正态分布。也就是说，因子的每个水平，其观察值是来自正态总体的简单随机样本。例如，在例7‐1中，要求每个行业的投诉次数服从正态分布。

（2）方差齐性（homogeneity variance）。各个总体的方差σ2必须相等。在例7‐1中，要求不同行业投诉次数的方差都相同。

（3）独立性（independence）。每个样本数据都来自不同水平的独立样本。在例7‐1中，要求4个样本数据是来自不同行业的4个独立样本。

7．1．3 使用SPSS进行单因子方差分析

在分析问题时，数据排列如表7‐1所示。但使用SPSS进行方差分析时，需要把“投诉次数”作为一个变量，排成一列，“行业”作为第二个变量，排成一列，对“投诉次数”进行分组。读入数据后：

（1）单击“分析”→“比较均值”→“单因素ANOVA”，系统弹出如图7‐1所示的对话框。

（2）选左框中的变量“投诉次数”，用箭头送入右边的“因变量列表”中，“行业”变量送入右边的“因子”框中。

（3）指定选项：

①单击“选项”按钮，弹出如图7‐2所示的“选项”对话框，选择“方差齐次性检验”选项。单击“继续”回到主对话框。

②单击“两两比较”按钮，弹出如图7‐3所示“两两比较”对话框，在“假定方差齐性”框中选择“LSD”。在“未假定方差齐性”框中选择“Tamhane's”。单击“继续”回到主对话框。

图7‐1 单因素方差分析主对话框

图7‐2 “单因素ANOVA：选项”对话框

图7‐3 “单因素ANOVA：两两比较”对话框

（4）单击“确定”，输出结果见表7‐2、表7‐3和表7‐4。

表7‐2 方差齐次性检验结果

表7‐2中，显著性概率P＝0．898，大于选定的显著性水平α＝0．05（系统默认显著性水平），表明4组数据具有方差齐性。Levene检验决定了如何读取表7‐4所示的多重比较结果。

表7‐3 方差分析表

表7‐3输出了方差分析统计量F的值为3．407，其显著性概率P＝0．039，小于选定的显著性水平α＝0．05。所以，应拒绝H0假设，即不同行业投诉次数有显著差异。

表7‐4 多重比较结果

* ：均值差的显著性水平为0．05。

表7‐4给出了LSD和Tamhane方法t检验的两两比较结果。由于Levene方差齐次性检验已经得出具有方差齐性的结论，所以这里应当读取具有方差齐性的LSD方法的检验结果。表中还用“*”标出了具有显著差异的均值。表7‐4中，行业3与行业4，即航空公司与家电制造业的投诉次数具有显著差异。

专栏

假设检验与方差分析

假设检验可用于两个总体均值的检验，对于多个总体，需要运用方差分析方法。现假定有4个总体均值分别为μ1、μ2、μ3、μ4，如果用一般假设检验方法（如t检验），一次只能研究两个样本，要检验4个总体均值是否相等，需要做6次检验，检验1：H0：μ1＝μ2；检验2：H0：μ1＝μ3；检验3：H0：μ1＝μ4；检验4：H4：μ2＝μ3；检验5：H5：μ2＝μ4；检验6：H6：μ3＝μ4。很显然，做这样的两两检验很麻烦。而且多次检验会导致犯第一类错误的概率累积增加。如果α＝0．05，6次检验会使犯第一类错误的概率达到1－1－α6＝0．265，而置信水平则降到0．956＝0．735。对多个总体而言，增加个体显著性检验的次数，偶然因素导致差别的可能性也会增加。而方差分析同时考虑所有样本，排除了累积错误的概率，提高了检验效率。

资料来源：陈在余，陶应虎．统计学原理与实务．北京：清华大学出版社，2009．