改变教学模式，全面准确地贯彻新教材的理念

改变教学模式，全面准确地贯彻新教材的理念

钟　敏

数学是人类的一种文化，它的内容、思想、方法和语言是现代文明的重要组成部分。教材中各种形式的丰富的阅读材料不仅提高学生学习数学的兴趣，拓展学生的知识面，同时也渗透了丰富的思想文化内涵，潜移默化地帮助学生提高思想觉悟和文化内涵。

教师不要轻看教材中如“七巧板”、“掷硬币”、“简单的图案设计”等看似游戏的教学素材，而要加以创新设计与用心组织，让“七巧板”课成为一堂玩具制作课、拼图设计课;让“掷硬币”课成为一堂数学实验课、数据统计分析课、数学史课;让“图案设计”课成为一堂折纸剪纸课、图案设计课、数学对称知识的应用课;又如“四边形的总结”课可以成为“学具制作”课(设计一种可以展示平行四边形、矩形、菱形、正方形、梯形的性质与判定的工具)。通过学生“做”、“学”、“创”的一系列数学活动，将大大促进学生数学探究性学习能力的发展。

关于数学史课的教学

新教材中数学的文化价值渗透到各部分内容中，采取多种形式，如与具体数学内容相结合或单独设置栏目做专题介绍或列出课外阅读的参考书目及相关资料源，以便学生自己查阅、收集整理。教材中的“读一读”文字材料介绍了大量的数学发展史以及古今中外著名数学家的故事。如:负数小史，介绍了最早采用正、负数表示相反意义的量，并进行负数运算的国家是中国;“代数”的由来，“代数(algebra)”最初来源于公元9世纪阿拉伯数学家、天文学家阿尔·花拉子米一本著作的名称，后被译成拉丁文传入欧洲，1859年，我国数学家李善兰首次把“algebra”译成“代数”;通过“耐人寻味的0．618”介绍了黄金分割的典型史料，反映其文化价值以及在人类历史上的作用影响，了解数学在相关学科的应用;还有“杨辉三角”、“方程小史”、“皮克公式”、“费马的失误”和“《几何原本》”等等。

在新课改的初中数学教学中，大多数教师都注重让学生掌握课程标准中规定的数学概念和结论，也注意到让学生了解所学知识的形成过程。但学生对数学发展的曲折历史知道很少，这不利于学生对数学知识的深入了解。“读一读”对这方面的内容做了一些弥补。如:通过阅读“无理数的发现”，使学生明白了真理是不可战胜的，古希腊人终于正视了为真理而献身的希伯索斯对无理数的发现，并进一步给予了证明，这一历史事实给人们的教育是非常深刻的。

“读一读”的这些内容向学生展示科学的广阔空间和对内容研究、思考的开放性，这样可以满足不同学生的需求，让他们在各自基础上都有不同程度的提高。所以在一些课前，可以布置学生通读阅读材料，使他们对材料所研究的内容产生兴趣，然后让他们趁热打铁预习一些新课，最后再运用相关知识去解决材料中提出的问题。如:通过“棋盘上的学问”来体会指数不断增加时，底数为2的幂的增长速度是惊人的;通过“画家自画像”来展示镜面对称在艺术创作中的应用等等。这些材料都是以实际生活作为展示平台，符合学生认知的心理特点，学生在学习有关知识的同时，能够体会到数学就在我们身边，数学与我们的生活密切相关，从而激发他们学习数学的热情，而每一材料中的每一个问题都具有一定的趣味性、目的性和挑战性，并且问题的设置处于学生思维的“最近发展区”，使不同层次的学生都能够有所收获，并使他们在成功中树立自信心，从而激发出浓厚的学习兴趣。

对于初中学生，榜样力量往往是无穷的，如教材中的“读一读”介绍了欧拉、费马、杨辉、赵爽等众多数学家的生平和事迹。当学完“完全平方公式”的代数解法后，笔者曾利用教材的阅读材料“杨辉三角”，介绍了宋朝的数学家杨辉的生平。并把这些材料与数学结合起来对学生进行道德、意志等方面的教育。让学生从中了解到我国古代的科学成就，不断树立起民族自豪感。经历了这方面的教育，不仅使学生有高度的爱国主义精神，也提高了数学课堂的境界，大大发挥了数学学科传播知识的功能，并培养和提高了学生的思想素质。

关于课例延伸

课例延伸的教学活动流程

①创设情境、提出问题:创设问题情境，是活动教学的起点和关键。创设的拓展问题情境必须注意问题的设计要具备启发性、探索性和开放性，既要让学生都能够探索和学习，达到基本要求;又要注意问题的层次性和研究价值，使学生在探究过程中实现知识的迁移、发展，形成新的认知结构。

②自主探究、尝试解决:这种以学生为中心的学习环境，打破了传统的教学方式和学习方式，由于这些拓展课程的问题设计具备可接受性和探究性，学生运用原有知识和方法发现和解决了教材以外的新内容、新问题，常常涌现出不同于教材、教师的新方法、新思路，因此这一过程不仅培养和发展了学生分析问题、解决问题的能力，而且能够使学生享受到创造的快乐，成为课堂拓展性学习的一次高潮。

③交流反馈，解疑释疑:学生通过演板、实物操作、计算机操作等方式向全班展示结果，进行交流，鼓励学生自我评价和学生之间互相评价，肯定结果指出不足，如果大多数学生解决问题有困难，还应抓住思维障碍适时适度启发。充分肯定学生的成绩，修正错误，同时也让他们体验到成功的喜悦，这也是课堂活动学习中必不可少的一部分。

④强化训练，迁移应用:可将题目分为三个层次:第一层次的题目是研究成果的直接再现;第二层次是研究成果的变式训练;第三层次是研究成果在新情境中的应用。其中前两个层次针对全班学生，第三层次针对学有余力的学生。

⑤反思小结，观点提炼:学生回顾新知识或新方法发生的大致过程，小结自己的学习收获，再由教师修正、补充说明，形成新的概念、公式、定理或结论，并引导学生提炼数学思想和方法。

⑥分层作业、自主发展:将作业分为必做题、选做题和思考题三个层次，学生可根据自己的学习水平去自行选择，有利于学生的自主发展。

教学案例:《蚂蚁怎样走最近》课例延伸

教学过程:

①创设情境，提出问题:

例1　如图，有一个圆柱体，它的高等于1 2厘米，底面半径等于3厘米，在圆柱下底面的A点有一只蚂蚁，它想吃到上底面与A点相对的B处的食物，需要爬行的最短路程是多少?(π的值取3)

例2　若把条件中的高由原来的1 2厘米改为3厘米，则最短路程又是多少?

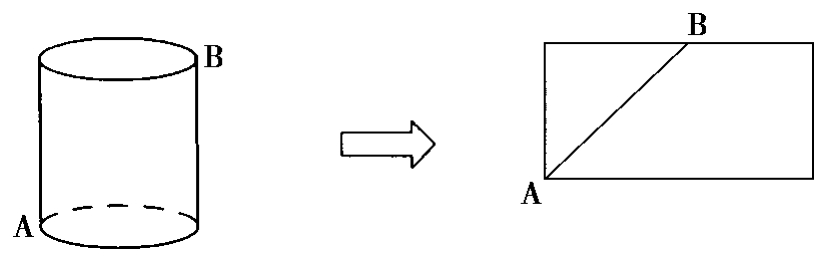
②自主探究，尝试解决:

例1源自课本例题，其内容和提问主要是让学生能自主的意识到此类(最短路程)问题可以通过将几何体展开成平面图形，利用几何原理“两点间距离最短”找出最短路径，最后通过勾股定理来解决问题．但常规教学下来我觉得学生通过此类问题的训练产生一种先入为主的感觉．似乎所有的立体图形中的“怎样走最近”的此类问题都只有将立体图形展开才能得到最短路径．实际上以上问题若把条件中的高由原来的12厘米改为3厘米，则会出现一条更短的路径，如图所示．

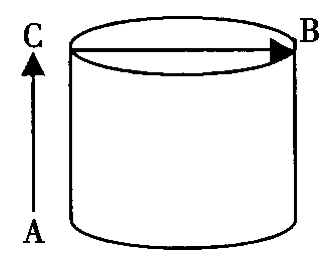
沿左图的A－C－B路径，路程长为9厘米．

若按原题展开圆柱体，计算侧面最短路径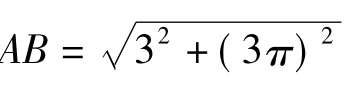≈9．89厘米＞9厘米

显然沿原立体图形A－C－B路径走路程会更短。

③交流反馈，解疑释疑:

何种情况下几何体的展开图形两点间的距离会更短呢?

设圆柱的高为h，半径为r，则由A－C－B的路径为h+2r;展开后AB的路径为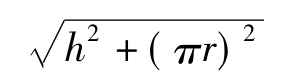

若两种方式的路程相等则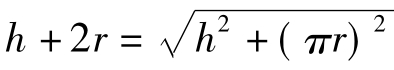，求得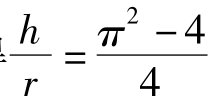

④强化训练，迁移应用:

例3一只蚂蚁在一块长方体的一个顶点A'处，食物在这个长方体上和蚂蚁相对的顶点C处，如图所示．已知长方体的长为6米，宽为5米，高为3米，蚂蚁急于吃到食物，沿着长方体的表面向上爬到C点，它们有长有短，蚂蚁究竟应沿着怎样的路线爬上去，所走的距离最短?你能帮蚂蚁求出最短距离吗?

分以上三种情况进行展开计算，比较结果，得出最短距离。

⑤反思小结，观点提炼:

问题的延伸与挖掘显然是让学生们感兴趣的，既丰富了学生的空间想象能力更进一步的拓展了思维运用能力。从一种思维方式到多种角度考虑的拓展，我不禁为学生们敏捷的思维感到骄傲。同时，也希望能在定量的计算转入到问题的定性分析上有所突破。特别是最后的长方体问题上，三种情况的考虑．显然每每遇到此类问题都对三种状况加以考虑并无不可之处，究竟何种展开方式能构造出最短路径呢?还应从三边的长度着手，利用字母表示三边长度，分三种情况进行讨论比较结果，得出结论。