改进的密封第一价格拍卖的博弈模型及均衡分析

穆　岚

2010210737上海财经大学统计与管理学院　概率论与数理统计硕士研究生

摘　要:本文在独立私有价值下讨论密封第一价格拍卖的纳什均衡,提出用三角形分布代替经典的均匀分布假设,并且在考虑交易费用、佣金,以及买主的风险偏好程度的条件下,给出买主的出价纳什均衡解。同时,分析了拍卖机制中交易费用、佣金比率及风险规避系数对本文得到的纳什均衡解的影响。研究表明,费用同出价成正相关,佣金比率同出价反相关,风险规避系数同出价反相关。

关键词:一级密封价格拍卖　纳什均衡　三角形分布　期望效用　风险规避

一、引言

拍卖是一种源于国外的交易机制,比如古董、艺术品等贵重商品的拍卖,又如政府的重大工程或者服务项目的招标,这两者虽然在金钱流向上体现出本质区别,但究其形式和操作上是有很多共同之处的。一般情况下,拍卖模型主要是基于两类市场机制,即可以分为完全信息拍卖和不完全信息拍卖。事实上,能够较好地符合现实社会的应该是不完全信息下的拍卖,但是这给理论研究带来了很多不确定性,因此目前的讨论主要是在不完全信息的两种极端情形下进行的。本文主要研究其中一种极端情形,即独立私有价值下的拍卖,也即每个参与拍卖的买主都清楚自己对拍卖品的私人评价,但是不知道别人的私人评价情况,而且各人的估计是相互独立的,每个买主的评价和其他买主的评价之间都不相关。

根据Vickrey的分类,有四大标准拍卖方式:荷兰式拍卖、密封第一价格拍卖、英国式拍卖和密封第二价格拍卖。[1]对这四种拍卖方式和两类拍卖机制的研究,目前主要有三类拍卖模型:对称的独立私有价值模型(Symmetric Independent Private Value)、共同价值模型(Common Value)和关联价值模型(Affiliated Value)。[2]国内外学者已经在拍卖理论和其他实际应用中取得很多成果,但是在拍卖模型建立中,大多是基于买主全为风险中性者,并且买主的私人评价独立共同分布于同一区间的均匀分布这种假设下的。这种基本假设虽然在一定程度上简化了模型,但是也偏离了现实社会。近来有学者对于均匀分布假设做了改进,提出了基于三角形分布下的密封第一价格拍卖博弈模型[3]。这种分布函数能够更好地符合买主这一理性人在拍卖过程中对于出价的一种趋众心理,然而该种模型依旧是基于经典的风险中性假设下的,而实际上买主们除了对同一标的物的私人评价不一样,在拍卖出价上的风险偏好程度也是不一致的,同时在拍卖中买主即便没有拍得商品,也是要付出一定的机会成本,就是要考虑交易费用以及拍卖商收取的佣金。

因此,本文试图考虑基于三角形分布、拍卖存在交易费用和佣金以及买主们的风险偏好度不相同等因素下,建立独立私有价值机制下的密封第一价格拍卖的出价策略博弈模型。通过这种对经典模型的改进,得到一种更加符合实际拍卖情况的均衡结果,以期给现实拍卖提供一些指导性建议。

二、模型建立

(一)基本假设

假设1　有n个买主,买主i视自己以及其余买主的私人评价为一个随机变量,买主们之间的私人评价相互独立,不受其他买主的估价影响,买主i的私人评价υi(i=1,2,…,n)独立且服从某同一区间的三角形分布。

假设3　如果买主没有获得拍卖品,需要缴纳的费用为f,其效用值为ω。拍卖商收取的佣金比率为t。

假设4　买主的风险偏好用效用函数u(x)来表征,其中u(x)>0,x表示收益。注意到若买主是风险中性的,则买主的效用函数为经典形式,即u(E(x))=E(u(x));若买主是风险规避型的,则u'>0,u″<0且u(E(x))>E(u(x));若买主是风险喜好型的,则u'>0,u″>0且u(E(x))<E(u(x))。

(二)密封第一价格的拍卖博弈模型

考虑独立私有价值拍卖建模,拍卖规则是密封第一价格拍卖。首先假设只有两个买主,应用对称性,这个博弈是建立在买主估计了另一买主的出价行为的条件下,才决定自己的最优出价策略(即纳什均衡)。也就是说,买主的最优出价策略应该是选择一个能使自己的期望支付最大化的出价,继而归纳推广到n个买主的一般情形。

又考虑到之前经典的均匀分布函数假设过于理想化,而正态分布在计算上又过于复杂,不具有实用性,因而采用三角形分布来近似代替正态分布。这种分布假设改进有两点好处:第一,密封第一价格拍卖实际上在出价上只与最高的价格有关,这种关于某一点的集中趋势,可以很好地被三角形分布模拟;第二,不像正态分布的密度函数那么复杂,三角形分布在理论证明上也给出了较为简单的结论。

针对这个模型,进一步假设买主i的私人评价υi服从区间(0,1)上的三角形分布,其密度函数为:

其中,a∈0,1()为随机变量的集中趋势。

1.风险中性假设下的纳什均衡

情况一:两买主模型建立。

考虑到对称性,不妨从买主i的角度着手,其支付函数为:

基于前面随机化假设,这个博弈问题是建立在买主i估计了买主j的出价行为的条件下,才决定自己的最优出价策略的。于是给定买主i的υ和b的情况下,其仅考虑交易费用的期望支付为:

若g(b)≤a,则其最优化条件为-注意到若是买主i的最优策略,则有g(b)=υ。即有:也即:

求解上述常微分方程得:

则(3)式即为该博弈问题在g(b)≤a下的纳什均衡。

若g(b)>a,同理可得解该常微分方程得:

则(4)式为此时的纳什均衡。

进一步,给定买主i的υ和b的情况下,其考虑交易费用和佣金的期望支付为:

若为纳什均衡。

若为纳什均衡。

情况二:n个买主模型建立。

由数学归纳的思想,在给定买主i的υ和b的情况下,考虑交易费用和佣金,买主i的支付期望支付为:

若为纳什均衡。

若为纳什均衡。

2.风险规避型买主的纳什均衡

假设买主的效用函数为其中yi=υi-bi,ri表示买主i的风险规避程度系数,0≤ri<1。关于风险规避型的效用函数有很多,顾梦迪[4]等人在文献中采用CARA效用函数,本文采用的是王则柯[1]所提及的效用函数,其中1-ri越小,表示买主i的风险规避程度越高,则其出价也越低。

为了便于计算,这里不妨直接写出其关于分布函数的纳什均衡形式解,这样的话,对于不同的分布假设均可以成立,并且在形式上也更加简练。若n个买主的密封第一价格拍卖,设买主i是风险规避型的,并且他的私人评价υi服从分布函数F(x),比如上文讨论的三角形分布,则在给定υ、b、r下,其效益期望为:

于是,同理可知其最优化条件为

令Y=(x-(1+t)b)1-r,解常微分方程得到,此时风险规避型的买主:

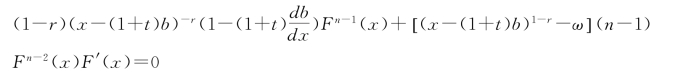
最优出价可以表示为:

(8)式即为风险规避型买主的纳什均衡。显然,买主的出价不会高于他的私人评价,由(8)式可知,当C为正时,上式满足条件b*≤υ,符合实际情况。而当风险规避系数r越逼近1时,则买主的出价越低;当佣金比率越高时,出价越低;参与拍卖的买主越多,出价越高,拍卖的交易费用越高,即ω越小,则出价越高。

三、纳什均衡的结论分析

由“风险中性假设下的纳什均衡”部分可知,考虑交易费用和佣金的条件下,n个风险中性的买主在密封第一价格拍卖下,基于三角形分布假设的拍卖出价的纳什均衡解可以表述为

若为纳什均衡。

若为纳什均衡。

当t=0,ω=0时,显然结论就是马国顺[3]等人所得到,但是本文认为实际交易机制下,需要考虑交易费用和佣金,这是对马国顺等人的结论的进一步完善。

这表明三角形分布代替均匀分布,使得卖主能获得买主相对较高的价值,同时买主也会考虑佣金和交易费用的存在,而出价相对低些。并且拍卖的交易费用越高,即ω越小,则出价越高。若收取佣金,t越大,则出价越低。当g(b)>a时,结论相同。

由“风险规避型买主的纳什均衡”部分知道,若买主是风险规避型,则由(8)式可知,当风险规避系数r越逼近1时,则买主的出价越低;当佣金比率越高时,出价越低;参与拍卖的买主越多,出价越高,拍卖的交易费用越高,即ω越小,则出价越高。

论文参考文献

1.王则柯、李杰:《博弈论教程》(第2版),中国人民大学出版社2010年版。

2.田国强:《现代经济学与金融学前沿发展》,商务印书馆2002年版。

3.马国顺、杨丽英、刘文文:基于三角形分布的一级密封价格拍卖博弈及均衡分析,《工业技术经济》,2010年第2期。

4.顾梦迪、李寿德、汪帆:排污权私人价值拍卖机制中风险规避型竞拍者的出价策略,《系统管理学报》,2009年第4期。

5.郑晓星:《拍卖导论》,上海社会科学院出版社2001年版。