温和的概念拉伸可将数学真理变为逻辑真理

（b）温和的概念拉伸可将数学真理变为逻辑真理

THETA：我以为Gamma说得对，确需要把合理的概念拉伸与不合理的概念拉伸区别开。因为概念拉伸历经了千山万水，已面目全非，已从温和的、理性的活动变成了激进的、非理性的活动。

原来，批评专集中于一个特定概念的轻微拉伸。它必须是轻微的，故而我们注意不到；若它的真正——拉伸的——本质暴露了它便可能不被接受为合法的批评。它全神贯注于一个特定概念，就像我们较为单纯的全称命题情况：“所有A都是B”。这里，批评意味着找到一个经轻微拉伸而又非B（我们的情况中是欧拉式的）的A（我们的情况中是多面体）。

但Kappa在两方面使问题尖锐起来。第一，使命题不止一个的构成成分经受概念拉伸式批评的攻击。第二，把概念拉伸从私下的并且相当谨慎的活动变成了概念的公开变形，如从“所有”到“没有之类的变形。这样，正受攻击之语词的任何有意义的改变，只要使定理为误，便一概算作反驳。我愿意采取这样的说法，如果不能就构成成分a、b、…把一个命题驳倒，则相对于这些构成成分而言，这命题是逻辑上为真的^[174]。这样的命题是一个长久的批判—思辨过程的归宿，在这个过程中，一部分语词的意义的重担完全转移到了其余语词和定理形式上。

如今Kappa的全部意思，只是说没有命题相对于其所有构成成分而言可以逻辑上为真。但可以存在相对于部分构成成分而言逻辑上为真的命题，从而反驳之洪流的再次泛滥，便只能在加上可拉伸的新构成成分之后方可。若我们一干到底，非理性主义便是我们的结局——但我们不需要一干到底。那么，我们应于何处划界？我们完全可以允许只针对构成成分中成为批评之靶心的突出子集来进行概念拉伸。逻辑真理不取决于它们的意义。

SIGMA：所以我们最终吸取了Kappa的论点：我们使真理至少是独立于某些语词的意义的！

THETA：言之有理。但我们若要击溃Kappa的怀疑主义，逃离他的恶无限，我们一到概念拉伸停止作为发展的工具而成为破坏的手段时，便自然不得不刹车了：我们也许得查明，仅有哪些语词的意义是可拉伸的，否则便要以摧毁理性的基本原理为代价^[175]。

KAPPA：你这套批判理性论的概念，我们能不能拉伸呢？莫非它是不言而喻得真，表述它的语词都是不可拉伸而又精确且不需要定义的吗？你的批评理论会不会吊着一个“以约定为退路”的尾巴是否每一事皆可批评，单单除了你的批评论、你的“元理论”^[176]？

OMEGA［向Epsilon说］：我不喜欢这种由真实性向合理性的转换。谁的理性？我感觉到了约定主义的渗透。

BETA：你们在谈论什么？我理解Theta说的概念拉伸的“温和模式”。我亦理解概念拉伸可以攻击不止一个的语词：当Kappa拉伸“拉伸”时，或者当Gamma拉伸“所有”时，我们就已经看到过了……

SIGMA：Gamma毫无疑问是拉伸了“单连通”！

BETA：可是他没有。“单连通”是个简称——他只是拉伸了出现在定义项中的“所有”一词^[177]。

THETA：回到这一点上来。你不满“公开”、激进的概念拉伸吗？

BETA：是。没有人要把这最后一类接受为真正的反驳！我很清楚，Pi曾揭示的探试批评的温和的概念拉伸的趋势，是数学发展中最重要的载体。但是数学家将永远不会接受这极端的、野蛮的反驳形式！

老师：此言差矣，Beta。他们确曾接受了它，并且他们之接受是数学史上的一个转折点。这一数学批评的革命改变了数学真理的概念，改变了数学证明的标准，改变了数学发展的模式^[178]！不过，现在我们要暂时结束我们的讨论：将在其他什么时间再讨论这一新阶段。

SIGMA：可这样便什么问题都还没解决好。我们此时此刻岂可撒手不管。

老师：我也有同感。这一最新阶段对我们的讨论会有重要的反馈^[179]。但是，科学的探究往往“开始于问题，也结束于问题”^[180]。［离开教室］

BETA：可开始时我哪有什么问题啊！现在我是除了问题一无所有了！

【注释】

[1]首先由欧拉（Euler）［1758a］注意到。他的原始问题是给多面体分类，其困难在其编辑总结中指出来了：“在平面几何中，多边形（figurae rectilineae）可依照它们的边数很轻易地分类，边的数目当然是等于角的数目的，但在立体几何中，多面体（corpora hedris planis inclusa）分类的难度便大得多了，因为仅有面的数目是不够的。”
欧拉得出他的结果的关键手段就是提出了顶点与棱的概念：是他首先指出，除面数外，多面体表面上的点的个数与线的条数亦决定其（拓扑）性质。有趣的是，一方面，他渴望强调他的概念框架的新颖性，强调他不得不发明“acies”（棱）一词以替代旧的“latus（边），因为latus是个多边形概念，而他想要一个属于多面体的概念；另一方面，他仍然为他的点状的顶点保留了“angulus solidus”（立体角）一词。最近普遍承认，此结果的优先权应归于笛卡儿（Descartes）。此说的根据在于笛卡儿的一份手稿［约1639］，由莱布尼茨（Leibniz）于1675年至1676年在巴黎抄自原稿，并由德卡莱尔（Foucher de Careil）于1860年重新发现并出版。不过，若没有一个小限定的话，优先权不应归于笛卡儿。不错，笛卡儿声称平面角数等于2φ＋2α－4，此处他以φ为面数，以α为立体角数。而且，他确亦声称平面角数是棱（latera）数的两倍。此两个命题结合起来，便得到欧拉式。但并未见及笛卡儿如此做，因为他仍然以角（平面的与立体的）与面进行思考，而并无自觉的革命性转变以零维的顶点、一维的棱与二维的面作为完全地刻画多面体拓扑性质的必要且充分的基础。

[2]欧拉相当彻底地对猜想就其结果进行了检验。他以棱柱、棱锥等等为例作了验算。他本还可以加上说，此一命题：仅存在5种正则立体，亦是猜想的一个结果。另一可疑的结论但是迄今为止才得到确证的命题是：4种颜色便足以绘制一张地图。
在V－E＋F＝2之例中，猜想与检验两阶段在波利亚（［1954］，卷1，第3章之前5节，第35－41页）中有所讨论。波利亚在此打住，并未处理证明阶段——虽然，他当然指出了对于解“证明题”的某种探试法的需要（［1945］，第144页）。我们的讨论自波利亚打住之处开始。

[3]欧拉（［1758a］，第119页与第124页）。但随后（［1758b］）他提出了一个证明。

[4]此一证明思想来自柯西［1813a］。

[5]19世纪许多数学家都与DELTA有同样看法：这个证明确立了此“定理”，使其无任何可疑之处，譬如克赖莱（Crelle）［1826—1827］，第2卷，第668—671页；马蒂森（Matthiessen）［1863］，第449页；德荣奎埃（Jonquières E.de）［1890a］及［1890b］。引用一段典型的话：“有了柯西证明，这一典雅的等式V＋F＝E＋2便可绝对毫无疑义地应用于所有种类的多面体了，正如欧拉1752年所说。所有的不确定性本在1811年就应当消失。”德荣奎埃［1890a］，第111—112页。

[6]这个班的水平相当高。对柯西、庞索特（Poinsot）及19世纪其他许多优秀的数学家而言，这些问题并未出现。

[7]思想实验（deiknymi）是数学证明最古老的形式。其在前欧几里得希腊数学中盛极一时（参考A·萨博（.Szabó）［1958］）。
对于古代数学家来说，在探试顺序中猜想（或定理）先于证明是一个常识。这可由“分析”相对于“综合”具有探试优先性推知。（一个出色的讨论，见罗宾逊（Robinson［1936］。）根据普罗克拉斯（Proclus），“……预先知道要找的是什么，是必要的”（希思（Heath）［1925］，卷Ⅰ，第129页）。“他们说，一个定理就是为了求其得证才提出来的”——帕普斯（Pappus）说（同上，卷Ⅰ，第10页）。希腊人对于他们在演绎路线中偶然想出而之前未曾猜中的命题，是瞧不起的。他们称其为不定设题、系定理、由定理之证明或问题之解决而得到的偶然结果，这些结果并非人们径直去寻求的，但不花费额外劳动便如其所是地偶然出现了，按普罗克拉斯所说，它们可以说是一种意外收获（ermaion）或好处（kerdos）（同上，Ⅰ，第278页）。我们在欧拉［1756—1757］的编辑总结中读到，算术定理“远在由严格的论证证实其真实性之前就发现了”。此一发现过程，编者与欧拉都以现代术语“归纳”相称，而不再用古语“分析”（同上）。在探试法上，结果先于论证、定理先于证明的观念，在数学的轶闻中有很深的根源。我们来引用同一个熟知的主题的几个变种传说克里斯帕斯（Chrysippus）曾写信给克利安西斯（Cleanthes）说：“只管把定理给我，接着我就会找到证明”（参见第欧根尼·拉尔修（Diogenes Laertius）［约200］，Ⅶ，第179页）传说高斯（Gauss）曾经抱怨说：“我已经得到我的结果多时了；可我尚不知我是怎样得到它们的”（参见阿伯尔（Arber）［1954］，第47页），又传黎曼（Riemann）也说：“真希望我有这些定理！如此我便可轻而易举地找到证明”（参见霍尔德（H9lder）［1924］，第487页）。波利亚强调说：“你必须在你证明一个数学定理前猜到它”（［1954］，第1卷，第vi页）。
“准实验”此词来源于前文提到的欧拉［1753］的编者总结。根据这位编者：“因为我们认为对数的思考肯定是纯粹的抽象思维能力的事，我们便几乎很难理解在探寻数的本质时观察与准实验能起怎样的作用。但是，事实上，如我要在这里以很好的理由展示的，今天所知的数的诸性质大部分是由观察发现的……”（波利亚的翻译；他在其［1954］，Ⅰ，第3页上错把引语归为欧拉的了）。

[8]鲁易里（Lhuilier）在以类似的方法改正欧拉证明时，说他仅做了一次“微不足道的观察”（［1812—1813a］，第179页）。但是，欧拉自己却放弃了证明，因为他见着了麻烦，而无法做那“微不足道的观察”。

[9]柯西以为，此一操作说明，即在每一步去找到一个或由移去两条棱边加一个顶点或由移去一条棱边而移走的三角形，可以施行于任意多面体是显而易见的（［1813a］，第79页）。这与他没有能力想象与球面不同胚的多面体有关。

[10]此反例1首先由鲁易里注意到（［1812—1813a］，第194页）。但编者日果内（Gergonne）附言上说（第186页），他本人注意到此反例远在鲁易里的文章发表之前。柯西却并非如此，他刚在一年前发表了他的证明。20年后此一反例又由赫塞尔（Hessel）发现（［1832］，第16页）。鲁易里与赫塞尔发现这个反例均是由矿物学采集所引起，他们于其间注意到了一些双晶体，这些双晶体的内晶是非透光的，而外晶却透光。鲁易里承认他的朋友皮克泰特（Pictet）教授的晶体采集对他有所刺激和影响（［1812—1813a］，第188页）。赫塞尔亦提到透光的氟化钙晶体所包住的硫化物立方晶体（［1832］，第16页）。

[11]定义1最先出现于18世纪；例如：“人们以多面立体（polyhedral solid）之名，或简单地以多面体（polyhedron）之名，称呼任何由平面（planes）或平的面（plane faces）围成的立体”（勒让德（Legendre）［1809］，第160页）。欧拉给出过相似的定义（［1758a］）。欧几里得在定义立方体、八面体、棱锥、棱柱时，并未定义多面体此一通名，但偶尔亦使用（如卷Ⅻ，问题二，命题17）。

[12]德荣奎埃针对那些欲驳倒欧拉定理之人，于法兰西科学院（French Academy）宣读了一些文章，我们发现定义2隐含在其中的一篇里。这些文章堪称怪物排除技术大全他向鲁易里那对畸形的嵌套立方体咆哮道：“如此一个系统不是真正的多面体，而只是一对彼此独立的不同多面体……一个多面体，至少从经典的观点看来，若要算名副其实的必须具备一个点可在其整个表面上连续移动的条件，而且此条件优先于其余一切条件；此处并不符合……所以鲁易里这第一个例外便可以弃之不管了”（［1890b］，第170页）。这个定义——与定义1相反——正合解析拓扑学的胃口，他们对多面体理论本身完全不感兴趣，而仅以其为曲面理论的陪衬物。

[13]反例2a及2b被鲁易里忽略了，只有赫塞尔才第1次发现它（［1832］，第13页）。

[14]在麦比乌斯（M9bius）（［1865］，第32页）中，定义3首次出现，是要排除孪生四面体。我们发现，他的臃肿定义以通常那种“要么接受，要么拒绝”的独裁口气在一些新式教科书中重新出现；其怪物排除之背景的来龙去脉——本来至少要解释一下——却并未谈及（如，希尔伯特与康佛森（Hilbert and Cohn－Vossen）［1956］，第290页）。

[15]定义P事实上是由R·巴策尔（R.Baltzer）建议的，据此则欧拉特性将成为多面体的定义特征。巴策尔说：“普通多面体有时（效仿赫塞尔）被称为欧拉多面体。为那些并非名副其实的（uneigentliche）多面体另找一个专名也许更合适”（［1862］，第2卷，第207页）。对赫塞尔的指涉是不公平的：赫塞尔使用“欧拉式的”一词仅是作为满足欧拉关系的多面体的缩写，想突出其与非欧拉多面体的区别（［1832］，第19页）。关于定义P，亦见下文脚注②所引施勒夫里（Schl9fli）的话。

[16]译注：海胆，约700种棘皮类动物（echinoderm）之通名，属海胆纲（Echinoidea）。其壳刚硬而呈球状，其表面覆有棘针，呈辐射对称状。形似开普勒之星状多面体。

[17]对“海胆”之讨论始于开普勒（Kepler）的宇宙理论（［1619］，第Ⅱ、ⅩⅨ及ⅩⅩⅥ册，第72页及第82—83页，与第Ⅴ册，第Ⅰ章，第293页，第Ⅲ章，第299页及第Ⅸ、ⅩLⅦ章）“海胆”之名出自开普勒的“以海胆名之”（cui nomen Echino feci）。图7由他的书中（第79页）复制而来，其书第293页尚有另一幅图。庞索特再次独立发现了海胆，正是他指出，欧拉公式对其不适用（［1810］，第48页）。现行的标准术语“小星状十二面体”是凯莱（Cayley）所取（［1859］，第125页）。施勒夫里承认了一般的星状多面体，但最终把我们的小星状十二面体当作怪物而拒绝接受了。据他说：“这不是货真价实的多面体，因它不能满足V－E＋F＝2的条件”（［1852］，§34）。

[18]多边形是否应被定义为包含星状多边形（按照定义4或者定义4′），这场争论已有很长时间了。我们的对话里提出的论据——当星状多边形嵌入一更高维的空间时，便成为普通多边形——是现代拓扑学论据，但还有许多其他的论据可以提出。比如，庞索特为其星状多面体辩护时，便以来自解析几何学的论据作为接受星状多边形的理由：“所有这些不同之处（“普通”与“星状”多边形之间）都是表面上的，比真正的不同更突出，一旦施行解析处理它们便彻底消失，因为此种处理中不同类的多边形是简直不可分的。正多边形的棱边对应实根方程，由方程同时得出同阶的所有正多边形的棱边。比如，若未同时找出第二、第三种七边形的棱边，则不可能得出一个内接于圆的正七边形的棱边。相反，已知某正七边形的棱边，便可决定其能内接的圆之半径，但如此做时，便会发现3个不同的圆，分别对应于在已知边上可作的3种七边形；其他多边形同理。那么，我们便可正当地以‘多边形’之名称呼这些新的星状图形”（［1810］，第26页）。施罗德（Schr9der）则采用了汉克尔式（Hankelian）的论据：“把最初仅限于整数的指数概念推广到有理分式，在代数学中硕果累累；这意味着只要机会一来，不论何时，我们在几何学中也应试试同样的做法……”（［1862］，第56页）。接着他说明了，我们也许可为星状多边形中p/q条棱边的多边形概念找到一个几何解释。

[19]Gamma声称他能够定义星状多边形的面积，这并非虚张声势。一些维护更宽泛的多边形概念的人，以提出一更宽泛的多边形面积概念解决了此问题。在正星状多边形的情况下，做法尤其明显。多边形的面积可取为内切圆或外接圆的圆心与各边连成的各等腰三角形之面积和。在此情况下，当然，星状多边形的某些“部分”会计算一次以上。对非正则多边形，我们得不到任何特异点，但仍可任取一原点，并以负定向的三角形之面积为负面积（迈斯特（Meister）［1771］，第179页）。结果看来——亦确实可以从“面积”预料出——如此定义的面积将不依赖原点的选取（麦比乌斯［1827］，第218页）。自然，有些人认为这样算出的数字算不上“面积”，于是可能有一场争论；不过，迈斯特－麦比乌斯定义的捍卫者却称其做“唯一（the）正确的定义”，“仅此是科学上正当合理的”（R·豪斯纳（R Haussner）的按语，［1906］第114—115页）。本质主义一直以来就是定义之争的永恒特征。

[20]我们在鲁易里的经典著作［1812—1813a］的第185页上亦发现了反例4——日果内又加上说他之前已知道了。但格龙奈特（Grunert）14年后还并不知道它（［1827］），庞索特45年后亦不知（［1858］，第67页）。

[21]此是意译自埃尔米特（Hermite）致斯蒂杰斯（Stieltjes）的一封信上的话：“这场无导数函数造成的不幸、可恶的瘟疫，所带来的厌恶与恐惧，让我痉挛着转过脸去”（［1893］）。

[22]“研究……违反了人们曾盼望是普遍适用的定律的函数，几乎均被视为闯入过去的先辈们寻求秩序与和谐的地盘里去宣传无序与混乱。”（萨克斯（Saks）［1933］，前言）萨克斯此处指的是在怪物排除者（如埃尔米特！）与反驳主义者之间的那场激烈争论，其于19世纪后几十年（亦确在20世纪之初）作为特征刻画了现代实变函数论这个“专跟反例打交道的数学分支”（芒罗（Munroe）［1953］，前言）的发展。之后又发生了在现代数理逻辑和集合论的反对者与倡导者之间盛行一时的同样激烈的斗争，这是那场争论的直接延续亦见第19页脚注①及脚注②。

[23]为让鲁易里带有隧道的多面体（画框）闪到一边去，不屈不挠的怪物排除者E·德荣奎埃提出了定义5：“按多面体一词的通常意义，此多面的复合体亦非一个真正的多面体，因若任取一正穿过立体的平面，其通过某个隧道中的任意一点，则得出的截面将是两个完全不连通的不同多边形；在普通多面体中，对于切割平面的某些位置，即是说在一些凹多面体中，此种情况亦会发生，但并非对所有位置均如此”（［1890b］，第170—171页）。人们想知道，德荣奎埃是否已注意到他的定义5也排除了一些凹的球性多面体。

[24]“我们必不能忘记，今日表现为怪物者，将是明日一条特定适应路线的发生原点……我要进一步强调虽稀有而极具意义的突变之重要性，这些突变影响着决定性胚胎发育过程的速率，其引起而产生者，人们不妨称为有希望的怪物，这些怪物若适应某个空置的合适的环境，便会引发一条新的进化路线。”（哥德施米特（Goldschmidt）［1933］，第544页及第547页）。我由卡尔·波普尔的提醒而注意此文。

[25]意译自庞加莱的话（［1908］，第131—132页）。完整的原文如下：“逻辑有时产生怪物。半个世纪来，我们已看见出现了一堆古怪的函数，它们似乎存心变得越不像那些有点用处的老实函数越好。不再有连续性，或也许有连续性，但没有导数，等等。尚不止此从逻辑的观点看，倒是这些奇怪的函数最具普适性，不找自来的那些函数反以特例的面目出现。它们仅保有一个非常小的角落。
“以前，一个新函数发明出来，是为了某个实用的目的；如今它们被专门发明出来，使我们的先辈们的推理变得不可靠，而除了这套，就没有什么其他东西可向它们请教。
“若逻辑成了教师的唯一导引，先讲最普适的函数便必要了，就是说要先讲最古怪的函数。初学者反不得不被迫与这畸形学博物馆搏斗……”（G·B·霍尔斯特德（G.B Halsted）授权译本，第435—456页）。庞加莱是就实变函数论中的情形讨论的此问题——但却无关紧要。

[26]套用当若依（Denjoy）的话（［1919］，第21页）。

[27]贝哈德（Bérard）［1818—1919］，第347页和第349页。

[28]赫塞尔［1832］，第13页。赫塞尔在1832年再次发现了鲁易里的几个“例外”他刚投出他的手稿，便撞见了鲁易里的［1812—1813a］。这样一来，虽然大部分结果是业已发表过的了，但他仍决定不撤回他的文章，因为他认为，应让忽视了这些例外的“晚近的学者们”接受这一论点。顺便提提，这些学者之一，恰巧是赫塞尔投稿的那家杂志的编辑：A·L·克赖莱。在其教科书［1826—1827］里他“证明了”欧拉定理对一切多面体为真（第2卷，第668—761页）。

[29]马蒂森（［1863］，第449页）。马蒂森此处是指海斯（Heis）和艾施外勒（Eschweiler）的《几何学教程》（Lehrbuch der Geometrie）及格龙奈特的《立体几何教程（Lehrbuch der Stereometrie）。然而，马蒂森并未——如Eta一般——以怪物排除法解决问题，却是——如Rho一般——用怪物校正法（参见第36页脚注①）。

[30]摘自柯西的杰作［1821］的引论。

[31]鲁易里和日果内似乎已肯定鲁易里的清单已历数了所有的例外。我们在此文这一部分的引论中读到：“人不难确信，对于所有多面体，不管凸与不凸，欧拉定理普遍为真除了我们将会指出的那些特例……”（鲁易里［1812—1813a］，第177页）。接着我们在日果内的评论中再次读到：“……这里所指出的例外似乎就是可能出现的全部……”（同前书，第188页）。但事实上，鲁易里遗漏了孪生四面体，只是在20年后才被赫塞尔注意到（［1832］）。值得注意的是，一些处于领导地位的数学家，甚至如日果内一样对方法论有浓厚兴趣的数学家，竟会相信人可依赖例外排除法。此一信念类似于归纳逻辑中的“分类法”，据此，可以完全枚举一个现象的所有可能解释，因此，若我们可通过判别实验（experimentum crucis）法排除某种解释之外的所有解释，剩下者便得到证明。

[32]I·牛顿［1717］，第380页。

[33]阿贝尔（Abel）［1826a］。他的批评看上去是直接针对欧拉式的归纳主义。

[34]这也是意译自所引的信中的话，信中阿贝尔谈的是如何把有关函数的一般“定理”的例外消除掉，由此而确立绝对的严格性。原文（包括前引一语）如下：“在高等分析学中，极少有命题是以确定的严格性来证明的。到处可以发现那由特殊至一般的可悲的方式，而惊奇的是，如此之手法要导出所谓的悖论，却极其罕见。找找原因倒确实很有意义我的看法是，其原因就在于这一事实：分析学家几乎总是考虑可表为幂级数的函数。只要他种函数出现了——当然这是极少出现的事情——便再也进行不下去了，并且只要开始得出了错误的结论，便有无限多的错误随之而来，互为依托……”（我加的斜体）。庞索特发现，归纳概括常常在多面体理论中失效，正如在数论中一样：“大多数性质是属于个体的，并不遵守任何一般规律”（［1810］，§45）。这种提防归纳法的心理的值得玩味的特征是它将归纳的偶尔失效归因于（事实的、数的、多面体的）领域中理所当然包含着超乎想像的例外。

[35]这又是在很大程度上与阿贝尔的方法如出一辙。以同样的方式，阿贝尔将有关函数的可疑定理之界域限制到幂级数。在欧拉猜想的故事里，限制到凸多面体的这类做法是相当普遍的。比如说，勒让德先给多面体下了一个较普遍的定义（参见第10页脚注①），随后提出一证明，这证明虽一方面决不适用于他的所有一般多面体，但另一方面却不止适用于凸多面体。然而，在一个补注中，他以小号字体（在意外发现了从未表述过的例外后的马后炮？）谦虚但安全地撤退到了凸多面体（［1809］，第161、164、228页）。

[36]不少实干的数学家感到困惑，若证明并不证明出什么，其又为的是什么？一方面，他们从经验得知，证明是可错的，但另一方面，他们从他们的教条主义的灌输中得知货真价实的证明必是不可错的。应用数学家通常以一条惭愧而坚定的信念摆脱这一两难困境，此信念即，纯粹数学家的证明是“完备的”，因而便是在真正地证明。不过，纯粹数学家们知道得更清楚——他们只对逻辑学家的“完备证明”有如此的尊敬。若问及他们的“不完备证明”之作用、功能是什么，他们中的大多数人便懵头转向了。譬如，G·H·哈代（G.H.Hardy）一百分地尊敬逻辑学家对于形式证明的要求，但当他想要以“我们从事研究的数学家所熟悉的方式”刻画数学证明之特征时，他采取了如下的方式：“严格说来，并无如数学证明者；在最后的分析中，我们仅指出些问题而已；……证明乃是李特伍德（Littlewood）与我所称为吹牛的东西，编出来打动人心的华丽辞藻，上课时黑板上的图画激发学生想象力的手法”（［1928］，第18页）。R·L·威尔德（R.L.Wilder）以为，“证明只是我们用于检验我们之直觉暗示的过程”（［1944］，第318页）。G·波利亚指出，证明者即便不完备，亦在诸数学事实之间建立了联系，这一点又帮助我们记住数学事实：证明最终产生了一个助忆法系统（［1945］，第190—191页）。

[37]马蒂森［1863］。

[38]此一论点：“海胆”“确”为一普通而平凡的欧拉多面体，有60个三角形面、90条棱、32个顶点——“无法描述的六十面体（un hexacontaèdre sansépithète）”，乃由欧拉定理之不可错之一坚定的支持者提出，此人即E·德荣奎埃（［1890a］，第115页）。不过，将非欧拉星状多面体解释为三角形化欧拉多面体的想法，绝非源于德荣奎埃，而另有一戏剧性的历史（参考下页的脚注①）。

[39]没有什么比教条主义认识论的错误论更具有其特点了。因为，若一些真理是显然的，便须解释怎么会有人在它们之上犯错误，换言之，为何真理并非对一切人皆是显然每一种教条主义认识论都根据各自特有的错误论，提供各自的特殊疗法，以清除思想中的错误。参见波普尔［1963a］，引论。

[40]庞索特肯定在1809年与1858年间的某个时候被洗脑了。正是重新发现了星状多面体的庞索特，从欧拉理论的角度首次分析了它们，并称，它们中的一部分，如同我们的小星状十二面体一样，是不遵从欧拉公式的（［1810］）。可是，这同一个庞索特却在其［1858中万分肯定地说，欧拉公式“不但对凸多面体为真，并且对无论什么多面体皆真，包括星状多面体”（第67页——庞索特用了特殊超常多面体（polyèdres d’espèce supérieure）一语指称星状多面体）。矛盾显而易见。怎样解释呢？星状多面体反例出了什么问题？线索就在此文看起来漫不经心的第一句话中：“可以将多面体的整个理论化为带三角形面的多面体理论。”即，庞索特－Alpha被洗脑后变成庞索特－Rho：他在曾经看见星状多边形的地方，现在只看得见三角形了；他在曾经看见反例的地方，现在只看得见例子了。这自我批评必是鬼鬼祟祟而隐蔽的，因为，按科学的惯例，如此的大变卦要如实招供是不成体统的。亦奇怪者是他曾否撞见环状面，若然，则他曾否心照不宣地以其三角形观点重新解释了它们？
视角之改变并不需要总是在同一方向上操作。譬如，J·C·贝克尔（J.C.Becker）在其［1869a］中——他被单连通域与多连通域的新概念框架给迷住了（黎曼［1851］）——虑及了环状多边形，却对星状多边形视若无睹（第66页）。此文发表后的5年——文中他曾声称已“确定地”解决了此问题——他扩展了视野，在之前只看见三角形与三角形化多面体处，又识别出星状多边形和星状多面体的图样了（［1874］）。

[41]此是斯多噶派错误论的一部分，归于克里西波（Chrysippos）的贡献（参见埃修斯（Aetius［约公元150］，Ⅳ.12.4；亦见塞克斯都·恩披里克（Sextus Empiricus）［约公元190］，Ⅰ.249）。据斯多噶派学者称，“海胆”为外部实在之一部分，于灵魂上留下烙印：phantasia或visum。一个智慧的人不会不加鉴别地赞成（synkatathesis或adsensus）phantasia，除非其成熟到清晰而分明的观念之程度（phantasia katalēptikē或comprehensio），而若其为伪，便不能成熟到这样的程度。清晰而分明的观念之系统形成科学（epistēmē）。在我们的例子中，“海胆”留于Alpha心灵上的烙印是小星状十二面体，而在Rho心灵上的烙印却是三角形化六十面体。Rho会断言，Alpha的星状多面体视像并不可能成熟到清晰而分明的观念的地步，原因显然是它会推翻那“已证”的欧拉公式。这样，星状多面体解释便招致失败，而“唯一的”替代品，即三角形化解释，便会变为清晰而分明的。

[42]此为怀疑派对于斯多噶派看法的一个标准批评，后者以为，他们可以分辨phantasia与phantasia katalēptikē（如塞克斯都·恩披里克［约公元190］，Ⅰ.405）。

[43]开普勒［1619］，册Ⅱ.命题ⅩⅩⅥ。（译注：Theophrastus Paracelsus，笔名Philippus Aureolus Paracelsus，原名Theophrastus Bombastus von Hohenheim，1493？—1541，瑞士医师、化学家，化学疗法奠基人，药理学之先驱，其著述虽不免巫术成分，然其于古代医学之批判，使医学走上一更科学之轨道。）

[44]这是在不偏不倚地陈述开普勒之观点。

[45]反例6是鲁易里注意到的（［1812—1813a］，第186页）；日果内此次破例承认了他的发现的新颖性！不过，几乎过了50年庞索特还没有听说过它（［1858］），而马蒂森（［1863］）乃至80年后的德荣奎埃（［1890b］）还把它当成怪物。（参见第29页脚注①及第36页脚注①）19世纪的原始例外排除者把它跟其他例外并列为古董：“作为例子，通常都举附在四面体一个面上的三棱锥，而前者之棱全无与后者重合者。我在大学笔记本里写道：‘真是奇怪，此情况下有V－E＋F＝3’。随后无话。”（马蒂森［1863］，第449页）。现代数学家渐渐忘记了环状面，它也许跟流形的分类无关，但在其他背景下便可能变为相关的。施坦豪斯（Steinhaus）在其［1960］里说：“我们把地球分成F个国家（海和洋都看成陆地）。于是，不论政治状况如何，总有V＋F＝E＋2”（第273页）。但令人好奇的是，施坦豪斯会不会单单因为西柏林（West Berlin）或圣马力诺（San Marino）的存在驳倒了欧拉定理，就把它们一举摧毁。（不过，他当然可以防止贝加尔（Baikal）一类的海整个落在一个国家里，方法是把它们都定义成湖，因为他说过，只有海和洋才看成陆地。）

[46]“……鲁易里的研究报告分为两个截然不同的部分。前一部分中，作者提出了欧拉定理一个新颖的证明。后一部分中，他的目标是指出这个定理所遇到的例外。”（日果内给鲁易里文章的编辑评论，见鲁易里［1812—1813a］，第172页，斜体由我所加。）
M·扎哈里阿斯（M.Zacharias）在其［1914—1931］里不加批判地但忠实地描述了这种分室隔离法：“在19世纪，几何学家除了寻找欧拉定理的新证明外，也参与确定它在某些条件下允许的例外。这类例外曾被叙及，如庞索特。S·鲁易里和F·Ch·赫塞尔则试图为例外分类……”（第1052页）。

[47]哈代、李特伍德、威尔德、波利亚似乎均忽略了这一点（见第26页脚注①）。

[48]译按：作者此处所用之improof一词，乃彼自造。彼于proof前加im－之前缀，一方表否定意，一方却以im＋proof所得之improof颇似improve一词，而讽其不断改进者译者求达其意，故以“只改不证”者译之。

[49]这一标准模式本质上是波利亚和舍戈（Szeg9）的经典著作［1927］描述的模式，在其第vii页上：“应仔细检查每一个证明，看看是否真正利用了全部假设；应努力从较少的假设得出相同结果……在反例显示出到达各种可能性的边界线前，不可自鸣得意。”

[50]用隐藏棱“焊接”两个多面体，是德荣奎埃主张的（［1890b］，第171—172页）。他以怪物排除反对空腔和隧道，而以怪物校正反对饰顶立方体和星状多面体。以怪物校正捍卫欧拉定理的首个倡导者是马蒂森［1863］。他自始至终使用怪物校正：他成功展示出隐藏的棱和面，解释了一切非欧拉多面体，包括带隧道和空腔的多面体在内。德荣奎埃的焊接是对环状面的彻底三角化，而马蒂森的焊接倒较为经济，他只画出能把面分为单连通子面的最小数目的棱（图14）。
马蒂森对其把实质性的反例转化为校正妥帖的重名的欧拉例子的方法，信心百倍他声称，“任意多面体都能分析成是对欧拉定理的确证……”。他历数浅薄的观察者指出的所谓例外，然后称：“任一这类的情况下，我们都可说明多面体有隐藏的棱和面，若把它们算在内，则定理V－E＋F＝2毫发无损，即令是对这些看起来桀骜不驯的情况亦如此。
然而，补画棱或面能使非欧拉多面体转变为欧拉多面体的这一想法并非出自马蒂森而源于赫塞尔。赫塞尔以3例为证，并配上了精美的图形（［1832］，第14—15页）。不过他并不以此方法“校正”例外，相反，他是要通过展示“能使欧拉定律生效的十分相似的多面体”，而“阐明例外”。

[51]这最后一条引理强得徒然无谓；若替之以引理“对拉伸及三角化过程得到的平面三角形化网状结构，有V－E＋F＝1”，对柯西证明的目的而言亦足够了。柯西似不曾注意到两者的区别。

[52]学生们显然通晓新近的社会哲学。此术语为波普尔所造（［1957］，第64页）。

[53]实际上，这样一个证明首由H·赖哈特（H.Reichardt）提出（［1941］，第23页）亦参见B·L·范德瓦尔登［1941］。希尔伯特和康佛森很满足于Gamma论断的真实性是“容易看出”的（［1932］，英译本，第292页）。

[54]波利亚（［1945］，第142页）。

[55]最后这句话出自艾丽丝·安布罗斯（Alice Ambrose）的趣文（［1959］，第438页）

[56]参见第5页脚注①。“拉链”的比喻是R·B·布莱思怀特发明的；然而，他只谈及“逻辑的”和“认识论的”拉链，而未谈及“探试法的”拉链（［1953］，尤其是在第352页）。

[57]海胆与圆柱均在前文讨论过了，第13页和第28—29页。

[58]守御定理的怪物排除是非形式数学里的重要模式：“使欧拉公式失效的例子有什么问题？为确保欧拉公式的有效性，要用哪些几何条件使F、V、E的意义更为精确？”（波利亚［1954］，第1卷，习题29）。圆柱是习题24里举的例。答案是：“……棱……应终止于角上……”（第225页）。波利亚将这话推而广之：“数学研究中不乏此一局面：定理虽已定型，而我们却还得赋给语词更精确的意义，使定理严格正确”（第55页）。

[59]定域而非全局的反例在第5—8页有所讨论。

[60]见第38页。

[61]见第31页。

[62]Gamma空洞的真陈述是19世纪一大创举。其问题背景（problem－background至今不明。

[63]“欧几里得……应用了一条他全未意识到的公理”（罗素［1903］，第407页）。”“作［sic］隐藏假设”是数学家与科学家的通用语。亦见伽莫夫（Gamow）对柯西证明的讨论（［1953］，第56页）或伊夫斯（Eves）和纽森姆（Newsom）对欧几里得的讨论（［1958］，第84页）。

[64]见第38—39页。

[65]非形式数学的优秀教科书通常会具体指出它们的“简略表达”项目，也就是它们认为平常得不值一提的或真或假的引理。对此的标准表述是：“我们假定读者熟悉x型引理”。随着批评使背景知识转化为知识，假定别人熟悉的分量便随之减少。比如，柯西竟未察觉他的名著［1821］预设了读者“熟悉”实数理论。任何反例，只要明白公开地表述出有关无理数性质的引理，他都会当作怪物拒绝。维尔斯特拉斯（Weierstrass）及其学派不复如此，所以，非形式数学教科书现在新辟了一章讲实数理论，其中收集了这些引理。但这些书的引言里又通常假定读者“熟悉有理数理论”。（例如，见哈代《纯数学》，第2版［1914］及以后各版。初版依然把实数理论归为背景知识；或见鲁丁（Rudin）［1953］。）更严格的教科书再进一步缩小了背景知识范围。朗道（Landau）在其有名的［1930］引言里假定读者只熟悉“逻辑推理和德语”。讽刺的是，正在同一时间，塔斯基表明了朗道那样略去的绝对平常的引理，可能不但为假，而且相互不一致——德语是语义封闭的语言。让人好奇的是，究竟“作者坦承自己对x领域无知”何时方取代一副权威气派的婉辞“作者假定人人熟悉x领域”：肯定只有到承认知识并无基础之时才行。

[66]当隐藏引理初次发现时，它被视为错误的。当贝克尔初次指出柯西证明（他引用的是巴策尔［1862］的二手证明）中的一个“隐藏”（stillschweigend）假设时，他称其为“错误”（［1869a］，第67—68页）。他提请大家注意，柯西认为所有多面体都是简单的：柯西的引理不但是隐藏的，而且是错误的。然而，历史学家无法想象伟大的数学家会犯这样的错误。在庞加莱［1908］里可以找到名副其实的伪造历史的手段：“不严格的证明什么也算不上。我以为没有人会对这个真理提出异议。但是，如果完全从字面理解，一字不放，我们便一定会得出这样的结论，如1820年前没有数学：这显然是过头了；那时代的几何学家是随意地理解我们要长篇大论才可解释的道理。这不等于说他们根本不懂；他们飞也似地就略过去了，而且，要懂透还需费饶舌之苦。”（第374页）贝克尔谈柯西“错误”的报告必得“1984－wise改写：“doubleplusungood refs unerrors rewrite fullwise”（见以下译按）。E·施坦尼茨（E.Steinitz做了改写工作，他坚持说，“欧拉定理并非普遍有效是不可能始终无人察觉的”（［1914—1931］第20页）。庞加莱本人也把他的手段应用于欧拉定理：“大家知道，欧拉曾证明了，对于凸多面体有V－E＋F＝2”（［1893］）——欧拉当然是对所有多面体陈述他的定理的。
译按：“1984－wise”与“doubleplusungood refs unerrors rewrite fullwise”是仿照英国小说家乔治·奥威尔（George Orwell，1903—1950）之名著《1984》中的新话原则（the Principles of Newspeak）写的。其书附录即“新话的原则”，专门介绍小说中大洋国（Occeania）的规定语言。大洋国即奥威尔氏假想之国，乃一极权主义之乌托邦。其书附录写道：“新话者，大洋国之官方语言，其所以发明是为了满足英社（英国社会主义）之意识形态需要。……形容词之形成，在名词兼动词之词后加－ful后缀；副词之形成，加－wise后缀。……任意单词……若表否定意，则加前缀un－；若表加强意，则加前缀plus－；若更进一步强调，则加前缀doubleplus－……”（《1984》，第237页以下，Penguin Books Ltd，1954年版，1987年印）。拉卡托斯此处所写之句，实是模仿《1984》第一部分第四章的这句话：“...doubleplusungood refs unpersons rewrite fullwise...”（同上书，第33页及第38页），奥威尔氏以现代英语自译为“...is extremely unsatisfactory and makes references to non－existent persons.Rewrite it in full...（……极为不妥，因其提到不存在的人。全部重写……）”（同上书，第38页）故拉卡托斯之“1984－wise”，即“1984式地”之意；其“doubleplusungood refs unerrors rewrite fullwise”，即“极为不妥，因其提到不存在的错误。全部重写”之意。

[67]见第27页。

[68]这个班的水平相当高——全局反例尚未出现，Alpha、Beta、Gamma就怀疑起3条引理了。在实际的历史中，证明分析好几十年后才到来：很长一段时期里，反例不是被当成怪物隐瞒起来或驱赶出去，就是被列为例外。从全局反例转向证明分析的探试进程——虚假性转送原理的应用——实际上在19世纪早期的非形式数学里是不为人知的。

[69]H·G·福德尔（H.G.Forder）［1927］，第viii页。或者说：“证明的一大优点是它们逐渐灌输对于已证结果的某种怀疑主义。”（罗素［1903］，第360页。他亦举了一个绝妙的例子。）

[70]众所周知，批评可以使人怀疑“先验真理”，甚至最后将其驳倒，从而使证明沦为仅仅只是解释。至于缺乏批评或反驳可以将似乎不合情理的猜想转化成“先验真理”，从而使试探性的解释转化为证明，这就不太为人所知了，但是同样重要。这种模式的两大事例便是欧几里得和牛顿的兴衰。衰落的故事尽人皆知，但兴起的故事通常都是误传的。
欧几里得几何像是作为一种宇宙论提出来的（参见波普尔［1952］，第187—189页）他的“公设”和“公理”（或称“公见”）当初是大胆而挑衅的命题，他们向巴门尼德（Parmenides）和芝诺（Zeno）宣战——据此两者的学说，这些“公设”不但是假的，甚至是逻辑上为假，不可思议的。事过多时，“公设”才被认为毋庸置疑地真，大胆的反巴门尼德“公理”（如“整体大于部分”）才被视为平常的，以致日后的证明分析略而不提，转化成了“隐藏引理”。这个过程始于亚里士多德：他给芝诺烙上了“好辩的怪人”的臭名，称其论证为“诡辩”。萨博最近以读来激动人心的细节披露了这一历程（［1960］，第65—84页）。萨博说明，在欧几里得时代，“公理”一词——如“公设”——是指批判的对话（dialectic）中的一种命题，要由推断就其结果进行检验，并不是已被讨论者承认为真的。这个词的意思刚好颠倒了，真是对历史的讽刺。欧几里得的权威在启蒙时期盛极一时。克莱洛（Clairaut）敦促其同行不要陈述明显的引理，以免“模糊了证明，搞烦了读者”：欧几里得之所以如此只是要叫“冥顽不灵的诡辩家”服气（［1741］，第x页和第xi页）。
牛顿的力学和引力论也是作为大胆的推测提出来的。莱布尼茨嘲笑之，并称其为“神秘的”（occult），连牛顿自己也颇感怀疑。但是，几十年后——没有反驳的情况下——他的公理就被奉为金科玉律了。疑点被遗忘了，批评被烙上了“古怪”之名，若还不至于“愚昧的话；他的一些最可疑的假定被视为平常的，连教科书亦从不提起。争论——从康德到庞加莱——不再是关于牛顿理论的真实性，却是关于确实性的本质了。（对牛顿理论的评价的大转弯是最先由卡尔·波普尔指出的——见其［1963a］各处。）
政治意识形态与科学理论的类似是远比一般的理解深邃的：起初大可争论的政治意识形态（可能只是强迫接受的），仅仅在一代的时间内，便可变成不容争辩的背景知识。批评者被遗忘了（也许被处决了），直到一场革命爆发，他们的异见才重见天日。

[71]这条规则似乎首次由P·L·赛德尔（P.L.Seidel）陈述过（［1847］，第383页）见后文，第147页。

[72]“我有权提出满足你的论据条件的任一例子，而你所称为古怪、荒谬的例子，我很疑心它们事实上正是些令人难堪的例子，是对你的定理不利的。”（G·达布（G.Darboux［1874b］）

[73]“隐藏引理的贮藏量使我觉得害怕，我不得不做大量的工作才能摆脱它们。”（G·达布［1883］）

[74]见第26页及第33—34页。

[75]庞加莱［1905］，第214页。

[76]同上书，第216页。“证明严格性”标准的几次改变引起了数学中的几次主要革命。毕达哥拉斯派（Pythagoreans）主张严格的证明必须是算术的。然而，他们发现了√2为“无理数”的一个严格证明。当这则丑闻最终传开后，标准改变了：算术“直觉”名誉扫地几何直觉取而代之。这意味着数学知识的一场重大而复杂的改组（例如：比例论）。18世纪，“易于误导的”图形使几何证明声名狼藉，而19世纪，算术直觉借棘手的实数论之助而重登王位。今天，主要的讨论阵地是，在集合论证明与元数学证明中，哪些严格而哪些不严格，譬如，众所周知的那场关于策梅罗（Zermelo）和干岑（Gentzen）的思想实验是否可被接纳的讨论。

[77]正如前文已指出的，这个班的水平很高。

[78]“心理主义”是胡塞尔（Husserl）造出来的术语（［1900］）。关于对心理主义的较早“批评”，见弗雷格（Frege）［1893］，第xv—xvi页。现代直觉主义（不像Alpha）公开拥抱心理主义：“数学定理表达纯经验的事实，即某一构造成功了……数学……是对人心的某些功能的研究。”（海丁（Heyting）［1956］，第8页及第10页）至于他们如何协调心理主义与确实性，他们严守秘密。

[79]即便我们有完美的知识，也无法完美地表述它，这对古代怀疑派本是老生常谈（见塞克斯都·恩披里克［约1900］，第83—88页），但在启蒙时期被遗忘了。直觉主义者重新发现了它：他们接受康德的数学哲学，但指出，“数学自身的真实完善性与数学语言的完善性之间看不出有什么清楚的联系”（布劳维尔（Brouwer）［1952］，第140页）。“经由口头语言或书写文字的表达——虽对交流必不可少——是永远不充分的……科学的任务不是研究语言，而是创造思想。”（海丁［1939］，第74—75页）

[80]布劳维尔［1952］，第141页。

[81]英语有“infinite regress”（无穷回归）一词，但这只是“恶无限”（schlechte Unendlichkeit）的一个特例，此处用不上。Alpha造这个短语显然是想到了“vicious circle”（恶性循环）。

[82]通常，数学家避免长定理的方法是通过选择加长定义的方式，使定理中只有被定义项（例如“普通多面体”）出现——这更加经济，因为一个定义缩写了许多定理。即使如此，按“严格的”解释，引出定义的怪物虽然极少提及，定义也占了极大篇幅。在福德尔［1927］中（第67页及第29页），“欧拉多面体”的定义（连同一部分定义项的定义）约占25行；在1962年版的大英百科全书中，“普通多面体”的定义填满了45行。

[83]“逻辑使我们拒绝某些论据，却不能使我们相信任何论据”（勒贝格（Lebesgue［1928］，第328页）。＊编者按：应当指出，按字面理解，勒贝格的陈述是错误的。现代逻辑为我们提供了有效性的一种精确描述，可以表明某些论据是满足这种描述的。可见，逻辑确实能让我们相信一个论证，尽管它也许不能让我们相信一个有效论证的结论——因为我们也许不相信某一个或更多的前提。

[84]E·H·摩尔（E.H.Moore）［1902］，第411页。

[85]“自然驳倒了怀疑主义者，理性驳倒了教条主义者”（帕斯卡［1659］，第1206—1207页）。少有数学家会像Beta那样坦承，理性太虚弱了，自身的正当性都提供不了。他们大多采纳某一类的教条主义、历史主义或混乱的实用主义，仍然古怪地无视这些是站不住脚的。例如：“数学真理事实上是全然不容争辩的知识的原型……但数学的严格性也不是绝对的；数学处在连续发展的过程中；数学原理不是一次就牢靠地凝成了，它们有自己的生活，甚至可以成为科学论争的主题。”（A·D·亚历山大罗夫（A.D.Aleksandrov［1956］，第7页）（这段引文可以提醒我们，辩证法试图不用批评来说明变化：真理“在连续发展之中”，但永远是“全然不容争辩的”。）

[86]编者按：我们相信，这条历史按语有些低估了数学“严格主义者”的成就。数学中向“严格性”的进军，最终暴露出来的，是向两个分隔的目标进军，其中只有一个可达。这两个目标，第一个是严格正确的论据或证明（其间真实性不可错地从前提传送到了结论上），第二个是严格为真的公理或第一原理（为的是从这个原点把真实性注入系统，然后经严格证明传遍整个数学）。第一个目标已知可达（当然要给定某些假设），而第二个已证不可达。
弗雷格和罗素设置了一些系统，数学能够（可错地）被翻译成这些系统（见后文，第122页），内中证明规则是有穷的，且已提前列为条件。结果证实，可以说明（刚才提到的假定于此处便可用）凡是用这些规则可证的命题都是该系统之公理的有效推论（即若公理为真，所证命题必亦为真）。在这些系统中，证明不得有“缺漏”，因而一串命题是否一个证明能够在有穷多步内检查清楚。（当然，若按检查结果，该公式序列不是我们考虑的系统中的证明，这并不足以确定结尾公式在该系统中没有货真价实的证明。所以，在证明检查过程中，有一种利于证实而不利于证伪的不对称性。）不论在哪一种严肃的意义上，都不能说这样的证明是可错的。（不错，也许凡是检查过某个这样的证明的人都犯了某种难以解释的错误，但这不算是严肃的怀疑。不错，这样的有效证明传送真实性此一非形式（元）定理也许是错误的——但这样想也没有什么严肃的理由。）可是，在非平常的意义上，这类系统的公理便确是可错的。从“自明的”、“逻辑的”真理推演出全部数学的企图业已破产，这是众所周知的。

[87]前文，第25页。

[88]关于第一件事例的讨论，见前文，第5—8页。

[89]Omega似乎漏了第三种可能性：Gamma完全可以说，既然局部而非全局的反例没有显示出任何对虚假性转送原理的破坏，便不需采取什么行动。

[90]参见前文，第46—47页。

[91]关于此处第二件事例的讨论，参见前文，第33—34页。

[92]见前文，第35—39页。

[93]见前文，第7页。

[94]同上。

[95]日果内证明在鲁易里［1812—1813a］第177—179页上。按原貌，它自然不会包含照相这一招。他说：“取一多面体，某一面是透明的；想象从外部把眼睛靠近这一面，近到能够感觉其他所有面的内部……”日果内谦虚地指出，柯西证明更加深入，它“有一个可贵的优点，就是根本不预先假定凸性”。（然而，他不曾想到要追问它的确预先假定了什么。）之后，雅各布·施坦纳（Jacob Steiner）重新发现了本质上相同的证明［1826］。那时有人提醒他将优先权归于日果内，他便读了鲁易里那篇附有例外清单的文章，但这并不妨碍他以此一定理为证明作结：“所有多面体都是欧拉多面体”。（正是施坦纳的文章激怒了赫塞尔——德国人的鲁易里——去写他的［1832］。）

[96]勒让德证明可在其［1803］中找到，证明引生的定理却找不到，因为在18世纪，证明分析和定理形成实际上是不为人知的。勒让德首先把多面体定义为表面由多边形面组成的立体（第161页）。接着他一般地证明了V－E＋F＝2（第228页）。不过，在第164页上以小号字体印刷的一条注里，又来了个例外除外式的修正，说是将只考虑凸多面体至于近乎凸的极端分子，他不予理会。庞索特在其［1809］里评勒让德证明时，最先注意到欧拉公式“并不仅仅对寻常的凸立体有效，即至多取两点便可用一直线切断其表面的立体：它对带凹角的多面体也成立，只要能在该立体内部找到一点作为球心，从此点引直线可将多面体的面投影到球面上，而投影各面不相重叠。这适用于无穷多的带凹角的多面体。事实上，就其本身情况而言，勒让德证明对所有这些另外的多面体也是适用的”（第46页）。

[97]E·德荣奎埃继续往下说，又是从庞索特［1858］剽取的一个论据：“祈求勒让德或相似的高级权威的保佑，只会助长一个广为散布的偏见，即欧拉定理的有效域只由凸多面体组成。这个偏见甚至把一些聪明绝顶的人都俘虏了。”（［1890a］，第111页）

[98]引自庞索特（［1858］，第70页）。

[99]D·M·Y·索末菲（D.M.Y.Sommerville）（［1929］，第143—144页）。

[100]开普勒曾设计了这个“大星状十二面体”（［1619］，第53页），庞索特又独立设计出来，且最先检验它是否是欧拉多面体。图15由开普勒的书中复制。

[101]我未能查到这段引文的出处。译按：伽利略《对话集》中，辛普利邱代表托勒密萨尔维阿蒂代表哥白尼，沙格列陀代表伽利略本人对前两人谈话作出的判断。

[102]参见第66页脚注①。

[103]全局而非局部的反例。

[104]全局兼局部的反例。

[105]答案就在著名的帕普斯古代探试法中，此种探试法只适合于发现“终极的”、“最终的”真理，即发现包含充分必要条件的定理。对“证明题”而言，此一探试法的主要规则是“如你有一猜想，由它引出推论。如你得到已知为假的推论，猜想便为假。如你得到已知为真的推论，倒转次序重推，若猜想能从此一真推论中引出，则其为真。”（参见希斯［1925］，第1卷，第138—139页。）“原因等于结果”（causa aequat effectu）的原理和对于包含充分必要条件的定理的追求，均由这种传统而来。只是到了17世纪——将帕普斯探试法应用于现代（modern）科学的种种努力悉数付诸东流——追求确定性才压倒了追求终极性。

[106]编者按：Epsilon纸条里的内容于后面的第2章揭晓。

[107]欧拉猜想尚有许多其他证明。关于欧拉、约当（Jordan）、庞加莱证明的详尽的探试法讨论，见拉卡托斯［1961］。

[108]庞索特、鲁易里、柯西、施坦纳、克赖莱都以为不同证明是在证明同一定理：“欧拉定理。”引一部标准教科书的典型语言：“这个定理来自欧拉，第一个证明出自勒让德，第二个出自柯西。”（克赖莱［1827］，第2卷，第671页）
当庞索特觉察出勒让德证明不仅仅可用于普通凸多面体时，他差不多就注意到区别了。（见第62页脚注①。）但当他随后对比勒让德证明和欧拉证明（基本点是切去多面体的棱锥角，最后得出一个四面体而不改变欧拉示性数）时，他却说勒让德证明较为可取，其理由是“简单性”［1858］。“简单性”代表18世纪的严格性观念：思想实验的清晰性。他不曾想到从内容上对比两种证明：这时会发觉欧拉证明更优越。（事实上，欧拉证明没什么错。勒让德应用了主观的那时代的严格性标准，忽略了客观的内容标准。）
鲁易里——暗中批评这段话（没提庞索特）时——指出勒让德的简单性只是“虚有其表”，因为它预设了大量的球面三角学背景知识（［1812—1813a］，第171页）。但鲁易里也相信勒让德与欧拉“证明的是同一定理”（同上书，第170页）。
雅各布·施坦纳跟他同样地评价勒让德证明，并同样地认定一切证明都在证明同一定理［1826］。唯一区别是，据施坦纳，不同证明证的是“所有多面体都是欧拉多面体”，而据鲁易里，不同证明证的是“所有无隧道、空腔、环状面的多面体都是欧拉多面体”。
柯西20岁出头就写了他论多面体的［1813a］，远在他的严格性革命之前。在其论文第二部分的引论里，他重复了庞索特对于欧拉证明和勒让德证明的对比，这不能看做是错误的。他——跟大多数同时代人一样——没有抓住不同证明在深度上的区别，因而不能认识到他自己的证明的真正威力。他以为，他还是只给出了同一定理的另一种证明——不过，他曾十分急切地强调，他得到了一个相当平常的概括，将欧拉公式又推广到某些多面体类。
日果内是认识到柯西证明举世无双的深刻性的第一人（鲁易里［1812—1813a］，第179页）。

[109]见第59页。

[110]同上。

[111]这个问题，鲁易里注意到了（［1812—1813a］，第189页），赫塞尔［1832］也独立地注意到了。在赫塞尔的文章中，两种画框的图是相互毗连的。亦参见第84页脚注①。

[112]波利亚称此为“发明者的悖论”（［1945］，第110页）。

[113]编者按：我们进教室之前，课堂上便讨论过这张表。

[114]见第76页脚注③。这张表借自波利亚［1954］，第1卷，第36页。

[115]见前文，第1页。

[116]这给第5页脚注①加了一层重要限制。

[117]波利亚［1954］，第1卷，第5页和第7页（我加的斜体）。

[118]见前文，第70—71页。

[119]这种试试错错的情景由波利亚漂亮地重建起来。第一个猜想是F随V增加。此被驳倒后，又有另两个猜想跟来：E随F增加；E随V增加。第四个是获胜的猜想：F＋V随E增加（［1954］，第1卷，第35—37页）。

[120]另一方面，因为数学通常用演绎的表述法，有些人又相信发现之路径是从公理和（或）定义到证明和定理。他们也许会完全忘掉素朴推测的可能性和重要性。实际上，在数学探试法里，演绎主义的危险性更大，而在科学探试法里则归纳主义的危险性更大。

[121]我们把数学探试法在本世纪的复兴归于波利亚的贡献。他那令人欣羡的工作的主要特色之一，是强调科学探试法与数学探试法之间的种种相似之处。唯一可能是他的弱点的地方也与此一强项联系在一起：他从不怀疑科学是归纳的，而由于他正确认识了科学探试法与数学探试法之间深刻的类似，他便不由自主地以为数学也是归纳的。同样的情况早先也在庞加莱身上发生过（见其［1902］，引言），亦曾发生在弗雷歇（Fréchet）身上（见其［1938］）。

[122]见前文，第39—40页。

[123]据帕普斯探试法，数学发现始于猜想，接着是分析，然后，在假定分析没有证伪猜想的情况，接着是综合（亦参见前文，第5页脚注①和第65页脚注①）。不过，我们这种版本的分析－综合是在改进猜想，而帕普斯版只是在证明或证伪它。

[124]参见罗宾逊（Robinson）［1936］，第471页。

[125]见前文，第20页。

[126]编者按：此一推理是错误的，虽然结论正确。黏合事实上造成了8个顶点、12条棱、6个面的消失。欧拉示性数便确因此减少了2。（图20（b）中，要假定两块阴影面完全重合，需颠倒其中一个半画框的倾斜方向，从而使宽棱与窄棱相交换。因为在此一操作下V、E、F都不改变，则论证实际上仍可通过。）

[127]此由拉什希（Raschig）［1891］做出。

[128]霍珀（Hoppe）［1879］，第102页。

[129]这又是帕普斯探试法的一部分。他把以猜想为起点的分析叫做“理论的”，把不以猜想为起点的分析叫做“悬疑的”（希斯（Heath）［1925］，第1卷，第138页）。前者涉及证明题，后者涉及求解题（或寻找题）。亦参见波利亚［1945］，第129—136页（“帕普斯”及第197—204页（“倒着做”）。

[130]“秩序”复原得力于鲁易里，他用了几乎同样的公式（［1812—1813a］，第189页）亦得力于赫塞尔，他用笨拙的专门公式来解释欧拉多面体的不同接合法（［1832］，第19—20页）。参见第69页脚注①。
从历史上说，鲁易里——在其［1812—1813a］中——曾经设法用素朴猜测来概括欧拉公式，并得到以下公式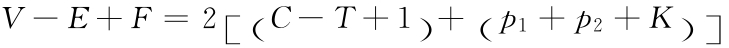：，此处，C为空腔数，T为隧道数，p_i为第i面上的内隐多边形数。只考虑“内隐多边形”时，他证明了它但隧道似乎就把他打败了。他构造这个公式是为了解释他的3种“例外”；但他的例外清单是不完整的（参见第23页脚注②）。而且，此一不完整性还不是他的素朴猜想为假的唯一理由：因他失察的可能性甚多，空腔也许是多连通的；在有分岔隧道的体系中，多面体的隧道数便也许无法单值地确定；有关的不是“内隐多边形数”而是环状面数（对共有一棱的两个相邻内隐多边形来说，他的公式便会破产）。关于对鲁易里的“归纳概括”的一个批评，见李斯丁（Listing）［1861］，第98—99页。亦参见第97页脚注①。

[131]19世纪有相当多的数学家被这类内容上的平庸增加手段弄糊涂了，确实不知道如何应对才好。有些人——如麦比乌斯——运用怪物排除定义（见前文，第12页）；还有些人——如霍珀——运用怪物校正。霍珀的［1879］尤其透露内情。一方面，他急切地——跟许多同代人一样——想要一个完备得无以复加的“广义欧拉公式”，它包罗万象。另一方面，一碰上平庸的复合物，他就畏缩不前了。所以，他尽管声称自己的公式是“完备的、一览无余的”，却又慌乱地加上说，“特殊情况会使（构成成分的）点查成为不确定的”（第103页）这就是说，如果哪个棘手的多面体还能打败他的公式，便是数错了它的构成成分，应该按正确的眼光来校正这个怪物：例如，孪生四面体的公共顶点和公共棱就一定要看两遍、数两次每一个孪生子多面体亦应自成一个多面体（同上）。关于更多的例子，参见第103页脚注②。

[132]见前文第49—53页。

[133]参见第103—104页。

[134]古代哲学家们毫不犹豫地把猜想从它的很平常的推论中演绎出来（例子可见我们从三角形到多面体的综合性证明）。柏拉图（Plato）以为“仅由一条公理也许就足以引生整个系统”。“通常来说，他以为单个假说就其自身而言便是可以结出果实的，他在他的方法论中忽略了其他并用的前提。”（罗宾逊［1953］，第168页）这便是古代非形式逻辑的特点，即证明的或思想实验的或构造的逻辑的特点；我们看出它是省略式，只是事后诸葛亮：内容的增加只是后来才变成推论脆弱的标志，而不再是推论强有力的标志。笛卡儿康德、庞加莱都全力鼓吹这种古代非形式逻辑；他们全部蔑视亚里士多德形式逻辑，说它贫瘠无果、无关紧要，然后把它们打发掉——同时又高歌多产的非形式逻辑之不可错性。

[135]庞加莱［1902］，第33页。

[136]19世纪中叶的数学批评才开始搜捕隐藏引理，这与稍后的证明分析取代证明、语言规律取代思维规律的过程有密切关系。逻辑理论最重要的发展通常是以数学批评的发展为先导的。不幸的是，即便那最优秀的逻辑史家也不免聚精会神于逻辑理论的变化而不注意它们的根源是在逻辑实践的变化中。亦参见第110页脚注②。

[137]见第80页。

[138]见第59页。

[139]见第49页。

[140]Alpha看来确实陷入了演绎探试法的谬论。参见第77页脚注①。

[141]笛卡儿［1628］，规则Ⅲ。

[142]见第39页。

[143]欧拉［1758a］的图6是几何教科书上出现的第一个凹多面体。勒让德在其［1809］里谈及了凸凹多面体。但在鲁易里之前谁也不曾提起过非简单的凹多面体。
然而，也许可以再加一层有趣的限制。最先被人研究的一类多面体有一部分是5种普通正多面体和棱锥、棱柱这样的准正则多面体（参见欧几里得）。文艺复兴以后，此一类多面体沿两个方向扩展了。一是正文指出的：把所有凸多面体和某些轻微凹陷的简单多面体包括进来。二是开普勒的方向：他发明了正星状多面体，由此扩展了正多面体类可是，开普勒的创举被遗忘了，只有等庞索特重来一次（参见前文，第12—14页）。欧拉肯定是梦里亦不曾与星状多面体相会过的。柯西知道它们，但他的心奇怪地隔离成两半了当他对星状多面体有了一个有趣的想法时，他便发表出来；但当他就自己的一般多面体定理考虑有哪些反例时，又忽略了星状多面体了。庞索特年轻时并非如此［1810］——但后来他改变了想法（参见前文，第29页）。
可见，Pi的说法虽然在探试法上是对的（即在理性的数学史中是正确的），但从历史上说却是错的。（我们不必为此担忧：实际历史往往是其理性重建的漫画化。）

[144]怪物包含定义的一个有趣的例子是庞索特为凸性重下的定义，此定义将星状多面体也收入了令人满意的凸正则立体类之中［1810］。

[145]这其实就是柯西的情况。倘使柯西那时已发现了他的革命性的例外排除法（见前文，第55—57页），他便有可能会去搜索例外，也会找到一些。但可能只是稍后，当他决心清除分析中的混乱时，他撞见了例外问题。（似是鲁易里最先注意到和正视了，这样的“混乱”并不限于分析。）
历史学家们，如施坦尼茨在其［1914—1931］中，通常说柯西注意到他的定理不是普遍有效的，故而只就凸多面体加以陈述。不错，柯西在其证明中使用了“多面体的凸表面”一语（［1813a］，第81页），在其［1813b］中于“立体角与凸多面体的若干定理”的总标题下重述了欧拉定理。不过，大概是想抵消这个标题，他尤其强调了欧拉定理对任何多面体的普遍有效性（第94页，定理Ⅺ），而把另外3个定理（定理⒔及其两个推论）明确针对凸多面体来表述（第96页及第98页）。
何以柯西用语这样马虎？柯西的多面体概念几乎与凸多面体概念重合。但又不完全重合：柯西知道凹多面体，它是可以在凸多面体一侧轻按一下便得到的，但是，他并不曾讨论何者看起来是对其定理不相干的进一步证实——而非反驳。（作为概念发展的催化剂，证实永远不能跟反例甚至“例外”相比。）柯西漫不经心地用了“凸”字的缘由正在于此意识到凹多面体可能有反例是一个失败，而消除这些反例并非有意识的努力。就在这同一段话里，他论证了欧拉定理是“对于平的多边形网状结构有V－E＋F＝1”这条引理的“直接推论”，并说“就V－E＋F＝1的有效性而言，各多边形是在同一平面上还是在不同平面上，这是无关紧要的，因为定理只涉及多边形数及其构成成分数”（第81页）。这个论证，在柯西狭隘的概念框架内完全正确，而在更宽的概念框架内却不正确，因其间“多面体”亦可指其他的，譬如种种画框。19世纪前半期，这个论据屡有重复（例如奥利维尔Olivier［1826］，第230页，或格龙奈特［1827］，第367页，或R·巴策尔［1860—1862］，第2卷，第207页）。J·C·贝克尔对其提出过批评（［1869a］，第68页）。经常是这样，只要概念拉伸驳倒了一个命题，被驳倒的命题似乎就立刻成了低级错误，而就简直无法想象伟大的数学家会犯这种错。概念拉伸式反驳的这个重要特征，解释了谦恭的历史学家们为什么给他们自己造出一大堆问题的混乱，因为他们不理解概念在发展。为了拯救柯西，谦恭的历史学家们声称他“绝不可能遗漏”非简单多面体，所以他“绝对地”（！）将定理限制到凸多面体的范围。但拯救之后，他们又不得不解释何以柯西的边界线窄得“徒然无谓”。何以他没有理会非凸欧拉多面体呢？施坦尼茨的解释是这样：欧拉公式的正确表述是要采用表面连通性的术语的。既然柯西时代尚未“清楚掌握”这个概念，那么“最简单的出路”就是假定凸性（第20页）。就这样，施坦尼茨把柯西从来没犯的一个过错给辩解掉了。
其他历史学家以另一种方式来拯救柯西。他们说，到达正确的概念框架（即他们知道的概念框架）的那一刻之前，只有一个“黑暗时代”，“即使不是没有，也是几乎没有可靠的结果。多面体理论的这一刻，据勒贝格说（［1923］，第59—60页）是约当的证明［1866a］而据贝尔（Bell）说（［1945］，第460页）是庞加莱的证明［1895］。

[146]见前文，第58页。

[147]参见第32页脚注①。

[148]达布在其［1874a］里差不多有了这个想法。后来庞加莱把它清楚地表述了出来：“……数学是以同名命名不同事物的艺术……如果语言选得合适，我们会惊奇地发现，给特定对象物体作的一切证明可立即用于许多新的对象物体；一切都不用改，甚至词语也不用改，因为名称已变成一样的了。”（［1908］，第375页）弗雷歇称此做法为“极其有用的概括原则”，并将它表述如下：“在证明有关某数学对象的某命题时，当证明使用的该对象的一组性质未确定该对象，这个命题便可扩展来应用于更一般的对象。”（［1928］，第18页）他指出，这样的概括不是平常的，“也许要花很大的力气”（同上）。

[149]柯西并未注意到这一点。他的证明与本书教师所给的证明在一个重要方面是不同的：柯西在其［1813a］和［1813b］里并未把多面体想象成由橡胶制成。他的证明思想的新意之处在于把多面体想象为一个面，而不再像欧几里得、欧拉、勒让德一样想象成一个立体。但他仍把它想象成一个立体的面。当他移去一面，把剩下的空间多边形网状结构映射为平面多边形网状结构时，他并没有把他的映射想象成拉伸，也许要把面和棱弄弯最先察觉到柯西证明可以施于带弯面的多面体上的数学家是克赖莱（［1826—1827］，第671—672页），但他仍然小心翼翼地跟着直棱走。然而，对于凯莱来说，似乎“第一眼”就能识破，“就算允许棱是曲线，这一理论也不会有本质的改变”（［1861］，第425页）。同样独立地觉察到的，有德国的李斯丁（［1861］，第99页），法国的约当（［1866a］，第39页）。

[150]这种概念形成论是把概念形成嫁给证明与反驳。波利亚则是把它嫁给了观察“当物理学家开始谈‘电’，或者医生们开始谈‘传染病’时，这些术语是含糊的、晦涩的、混乱的。科学家今天所用的术语，如‘电荷’、‘电流’、‘真菌传染’、‘病毒传染’，就较为清晰较为确切，不可同日而语了。不过，两套术语之间，及一些重大发现之间，都经过了大量的观察、多少精巧的实验啊。归纳改变了术语，澄清了概念。整个过程的这一方面，对概念的归纳澄清，我们也能在数学中的示例说明之。”（［1954］，第1卷，第55页）但即便是这种错误的归纳主义概念形成论，也比把概念形成说成是自律的，把概念的“澄清”或“说明说成任何科学讨论的预备阶段要更可取。

[151]见前文，第68页。

[152]霍布斯［1656］，对主教第xxi条答复的批驳。

[153]见前文，第66页脚注①。

[154]跟着从相当素朴的多面体分类到高度理论的分类的逐渐变化，亲身体验一下是有趣的。第一个不再仅仅容纳简单多面体的素朴分类，出自鲁易里：一个根据空腔、隧道和“内隐多边形”的数目作的分类（见第84页脚注①）。
（a）空腔。欧拉的第一个证明，顺便说说，还有鲁易里自己的证明（［1812—1813a］第174—177页），都立足于对立体的分解，方法要么是把它的角一个个切掉，要么是从内部的一点或几点把它分解成棱锥。然而，柯西证明——鲁易里并不知道它——立足于对多面形曲面的分解。等到多面形曲面论最终取代多面立体论之后，空腔便让人厌倦了一个“带空腔的多面体”变成了整个多面体类。于是，我们的老怪物排除定义2（第11页变成证明引生的理论定义了，“空腔”这个分类学概念从发展的主流中消失了。
（b）隧道。李斯丁已指出此一概念不尽如人意（见第84页脚注①）。它之被取代，并非如卡尔纳普派学者所期望的，是由于对“隧道”这个“含混”概念的任何“说明”，而是由于试图证明和反驳鲁易里对带隧道的多面体的欧拉示性数提出的素朴猜想。在这个过程中，带n条隧道的多面体概念消失了，证明引生的“多连通性”（我们所称的“n球性”）取而代之。我们发现，某些文章还在沿用这个素朴术语来指称证明引生的新概念：霍珀把“隧道”数定义为使多面体成为连通的所需切割的数目（［1879］，第102页）。在恩斯特·施坦尼茨看来，隧道概念在理论上已如此饱和，以致他无法查明，鲁易里按隧道数作的素朴分类与证明引生的按多连通性作的分类有什么“本质”区别；所以，他以为李斯丁对鲁易里分类法的批评“非常不公正”（［1914—1931］，第22页）。
（c）“内隐多边形”。这个素朴概念也是不久即被环状面取代，随后又被多连通面取代（亦参见第84页脚注①），（是取代而非“说明”，因为“环状面”肯定不是对“内隐多边形的说明）。然而，当多面曲面论一面被拓扑曲面论所取代，一面又被图论所取代时，多连通面如何影响多面体的欧拉示性数的问题也就失去其所有意义了。
可见，第一个素朴分类的3个关键概念当中，只有一个“留下来”，而即使这一个也难以识别了——广义欧拉公式暂时被简化为V－E＋F＝2－2n了。（关于进一步的发展参见第94页脚注③。）

[155]只就素朴分类而言，唯名论者接近真理，因他们以为各种多面体的唯一共同点便是它们的名字。但是在几个世纪的证明与反驳之后，随着多面体理论的发展，理论分类取代了素朴分类，天平就倾向于实在论者了。带有普遍性的问题应当基于这一种事实重新考虑：随着知识的发展，语言亦在变化。

[156]菲利克斯（Félix）［1957］，第10页。按照逻辑实证主义者的观点，哲学的专一任务便是构造“形式化”语言，来表达科学的人工凝固状态（见我们前面所引用的卡尔纳普的话，第1页）。但是，在科学的快速生长抛弃了旧的“语言系统”之前，这样的研究是几乎不可能进行的。科学教我们不要遵奉任何给定的概念—语言框架，以免它变成概念囚笼——对这个过程，语言分析学家有一种至少想延缓它的既定兴趣，以说明他们那套语言疗法的正当性，即是说，想显示出他们对科学有至关重要的反馈和价值，以及他们并没有正在堕落为“相当干瘪的委琐老顽固”（爱因斯坦Einstein［1953］）。波普尔曾对逻辑实证主义提出过与此相似的批评：例如，见其［1959］，第128页，脚注＊③。

[157]波利亚区分“简单的”和“苛刻的”检验。“苛刻的”检验也许会给出“证明的初步线索”（［1954］，第1卷，第34—40页）。

[158]“一般的情况可以在逻辑上等价于特殊情况，这在数学里简直是司空见惯的事情，但在初学者看来，或者在自命高深的哲学家看来，却仍然是令人惊讶的”（波利亚［1954］，第1卷，第17页），这话在非形式逻辑里一点不错。亦参见庞加莱［1902］，第31—33页。

[159]凯莱［1961］和李斯丁［1861］严肃地对待多面体理论基本概念的拉伸。凯莱把棱定义为“从一顶点到它自身或任何其他顶点的路径”，但又允许棱退化成无顶点的闭曲线他称为“围线”（第426页）。李斯丁有一个术语“线”（第104页）指各种棱，不论其顶点是两个、一个还是没有。他们两人都知道，他们慷慨大方的概念框架里接纳的“畸形物”，需要全新的理论才可解释——凯莱首创了“闭图形划分理论”，现代拓扑学伟大先驱之一的李斯丁发明了“空间复形普查”。

[160]见前文，第27—31页与第36—38页。

[161]不少数学家不能区别平常与不平常。不但缺乏寻觅有效信息的感觉，而且还幻想能构造一个非常完备的公式将所有可想到的情况都包括在内，这就特别狼狈（参见第84页脚注②）。这样的数学家可以为一个公式的“最终”概括而努力多年，末了也就不过作了几处平常的修改来做推广。优秀的数学家J·C·贝克尔就提供了一个逗人的例子他努力多年之后，提出了V－E＋F＝2－2n＋q这个公式，此处n是把多面体表面分成满足V－E＋F＝1的单连通面所需的切割数，q是把所有面化为单连通面所要添上的对角线数（［1869a］，第72页）。他很为其成就自豪，声称它发出“全新的光彩”，甚至“终结了“像笛卡儿、欧拉、柯西、日果内、勒让德、格龙奈特、冯·施陶特（von Staudt）这类人物都热心研究过的课题”（第65页）。可是，他的阅读书目里漏了3个名字：鲁易里、约当、李斯丁。当他被告知了鲁易里的情况后，他加上了一条沮丧的注释，承认鲁易里50多年前就知道这一切了。至于约当，他对环状面是没什么兴趣的，但碰巧对带边界的开多面体感兴趣，所以，他的公式里除了n，还有边界数m（［1866b］，第86页）。于是，贝克尔——在一篇新文章［1869b］里——就把鲁易里和约当的公式综合成V－E＋F＝2－2n＋q＋m（第343页）。但贝克尔在困窘中太过草率，未能消化李斯丁的长文。所以，他在［1869b］中沮丧地得出结论：“李斯丁的概括范围还更广。”（顺便提一下，他后来又试图把他的公式也推广到星状多面体［1874］；参见前文，第29页脚注①。）

[162]有人也许持俗人之见，以为有一条反驳收益递减律。Gamma自己确无此念。我们现在将不讨论单侧多面体（麦比乌斯［1865］）或n维多面体（施勒夫里［1852］）。这些例子会证实Gamma的期待，就是完全出乎意料的概念拉伸的反驳总是可以给整个理论一种新的——可能是革命性的——推动。

[163]波利亚指出，浅薄而廉价的概括“在今天比过去更时髦了。一点小想法，就拿一个大术语来稀释。就连这点小想法，作者通常也宁愿从别人那里拿过来，忍住不补充任何原创性的观察，避免解决任何问题，除了他自己的术语困难产生出了问题。这很容易举出例子，但我不想与人有忤”（［1954］，第1卷，第30页）。当代另一个最伟大的数学家约翰·冯·诺伊曼（John von Neumann）也警告大家提防这种“退化的危险”，但是他认为“只要这门学科处在有超常素质有品位的人的影响下”，情况就不至于太坏（［1947］，第196页）。不过，人们想知道的是，若是在我们这个“要么发表，要么消失”的时代，“有超常素质的高品位者的影响”是否就足以拯救数学了。

[164]见前文，第53页。

[165]同上。

[166]实则Alpha不曾公开使用过这个波普尔派术语；见前文，第17—18页。

[167]见前文，§4（b）。

[168]见前文，§5。

[169]见前文，第41—45页。

[170]编者按：Kappa声称含混性不可避免是对的（某些术语一定要是基本的）。但他却误认为这意味着总是可以通过“概念拉伸”来制造反例。按定义，一个有效的证明就是无论如何解释其描述性术语，亦永远造不出反例——即证明的有效性并不依赖于描述性术语的意义，故而可以随意地拉伸它们。此是由拉卡托斯本人指出的，见下文，第110页，又见（更有条理的）第2章，第134页。

[171]参见菲利克斯［1957］，第9页。

[172]Gamma要求给“反例”下个如水晶般清澈的定义，这不啻要求元语言中有如水晶般清澈的无伸缩性概念作为理性讨论的条件。

[173]阿诺德（Arnauld）和尼科勒（Nicole）［1724］，第xx—xxi页。

[174]这是对波尔察诺（Bolzano）的逻辑真理定义稍加改写的版本（［1837］，§147）。何以波尔察诺在19世纪30年代提出了他的定义，是个费解的问题，尤其是他的工作竟预期了模型概念，而后者是19世纪数理哲学的最伟大创举之一，这就更费解了。

[175]19世纪的数学批评拉伸了越来越多的概念，把越来越多的语词的意义重担转移到了命题的逻辑形式和少数（当时还）未拉伸的语词之意义上。20世纪30年代，这个过程似乎慢了下来，不可拉伸语词（“逻辑”语词）与可拉伸语词（“描述”语词）之间的分界线似乎变得稳定了。一份只包含少量逻辑语词的清单达成了广泛的认同，于是便可能为逻辑真理下一个一般的定义；逻辑真理不再是“相对于”专门的构成成分的清单了。（参见塔斯基［1935］）然而，塔斯基为这种分界线感到迷惑，想弄清它是否最终不得不回到一个相对化的反例概念，从而回到一个相对化的逻辑真理概念（第420页）——像波尔察诺的一样，顺便提一句，塔斯基并不知道有这回事。这个方向上最有趣的结果是波普尔的［1947—1948］，由此可知，若不放弃理性讨论的某些基本原则，便不能放弃更进一步的逻辑常项。

[176]“以约定为退路”是巴特利（Bartley）的用语［1962］。他主要是从宗教知识的角度，研究是否可能为批判理性主义作合理辩护的问题——但是从数学知识的角度，问题模式几乎相同。

[177]见前文，第41—45页。Gamma事实上却想从“所有”上移除一些意义的负担，使其不再只适用于非空的类。通过从“所有”的意义中移除“存在的意义输入”这种谨慎适度的拉伸，使空集从怪物转化为寻常的平庸集合，这是一个重要事件——不仅关涉到对亚里士多德逻辑进行布尔逻辑的集合论的重新解释，亦关涉到数学讨论中空洞的满足这一概念的出现。

[178]批评、反例、推论、真理、证明的概念是不可分开的；它们起变化时，最先变的是批评概念，然后其他概念随之而变。

[179]参见拉卡托斯［1962］。

[180]波普尔［1963b］，第968页。