拓扑传播学初探

拓扑传播学初探⁽¹⁾

[内容提要]　本文将拓扑学方法应用传播学，开辟了传播学的一个新方向——拓扑传播学。本文给出了信息传播渠道的一个严格数学定义，分别讨论了不同传播渠道和不同传播空间之间的同伦关系，证明了渠道同伦和传播空间同伦都是等价关系。据此，可以对不同传播渠道和不同传播空间进行等价聚类。最后讨论了可形成“舆论点”与“舆论区域”的传播空间特点，得出了“舆论”的一个严格数学定义，提出了舆论是一种数学映射的观点，并给出了舆论形成的充分必要条件。通过本文首先把Osgood传播系统看作是一个拓扑空间，在此基础上建立了Osgood传播系统的基本群模型，较为详细地讨论了Osgood传播系统的拓扑性质，得出了两点重要推论：一是Osgood传播系统的基本解是拓扑不变量；二是可形成舆论的Osgood传播系统是单连通的。

[关键词]　传播空间　拓扑　同伦　舆论　Osgood传播系统基本群

一、信息传播渠道

根据申农（shannon）信息传播模型，信息发送者、信息接收者和信息传播渠道是信息传播的三大基本要素，我们首先定义信息传播渠道开始我们的讨论。

定义1（信息传播渠道）设X是由信息发送者和接收者构成的拓扑空间，a为信息的发送者，b为信息的接收者，如果存在一个连续的映射：σ：I→X，满足σ（0）＝a，σ（1）＝b，则称σ为从a到b的一个传播渠道，这里I＝[0，1]。

设σ：I→X，是X中从信息发送者a到接收者b的一个传播渠道，则由σ（t）=σ（1-t），t∈I，定义的σ的逆道。σ：I→X是指X中从信息接收者b到信息传播者a的信息反馈渠道。根据传播渠道的这种对称性，我们也称σ为连接信息发送者a和信息接收者b的一个信息传播渠道，而无需指明a和b哪一个是信息的发送者和信息的接收者。

应当着重指出的是，上面定义的信息传播渠道是一个映射，而不是映射的像？（I）。例如，根据信息传播渠道的定义，由σ （t）=t，t∈I确定的映射σ：I→R1和由Γ（t）＝t2所确定的映射σ：I→R1都所是连结0和1的信息传播渠道，但它们是两个不同的映射，因而是0和1之间的两个不同的信息传播渠道。但如果只看映射像，显然有σ（X）＝Γ（I）＝σ（I）。

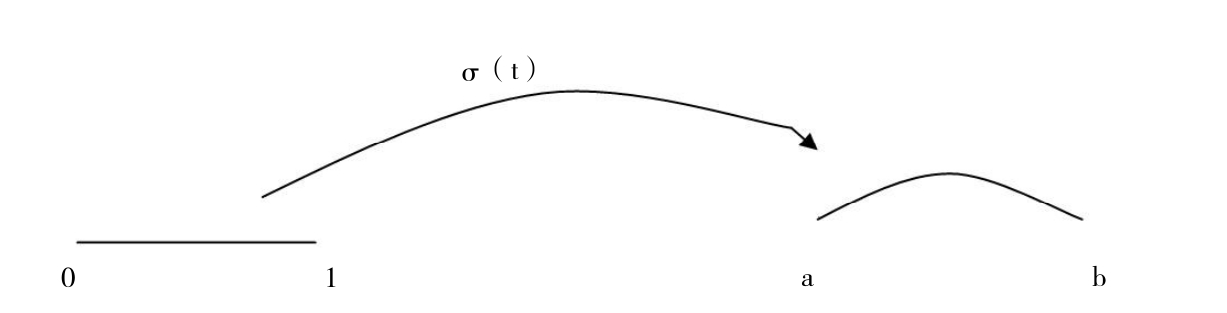
图-1　信息传播渠道示意图

二、信息传播渠道的同伦

从数学上讲，上节中定义的信息传播渠道是指定义在闭区间I＝[0，1]上的一个连续映射。现在我们考虑更为一般的情况，即信息传播渠道的同伦问题。

为了研究信息传播渠道的同伦问题，我们要拓宽研究范围，考虑一般的连续映射的情况。设X和分别是由信息发送者和信息接收者组成的拓扑空间，f，g：X→Y是从X到Y的两个连续映射或者两个信息传播渠道。我们先来分析一下f连续地形变为g是什么意思。直观上，f连续地形变为g可以看成有一族以t∈ [0，1]为参数的连续映射（信息传播渠道）｛ft：X→Y：t∈[0，1]｝使得f0 ＝f1， f1=g。这里要求当t在区间I上连续变动时，ft依一种连续的方式变动。也就是说，ft（x）同时连续地依赖于t∈I 和x∈X。所以，如果存在一个连续映射F：X×I→Y使得F（t，x）＝ft （X），t∈I，x∈X的话，F的连续性可描述信息传播渠道的连续形变ft。

定义2（信息传播渠道的同伦）设X和Y分别是由信息发送者和信息接收者组成的拓扑空间，g⁰，g¹：X→Y是连续映射，为两条不同的信息传播渠道。如果存在连续映射F：X×I→Y使得对所有x∈X成立，F（x，0）＝g⁰（x），F（x，1）=g¹（x）,我们就说信息传播渠道g⁰同伦于信息传播渠道g1，记作F：g⁰≌g¹：X→Y，或简记为F：g⁰≌g¹。这时，称F为从信息传播渠道g⁰到g¹的一个同伦或伦移。

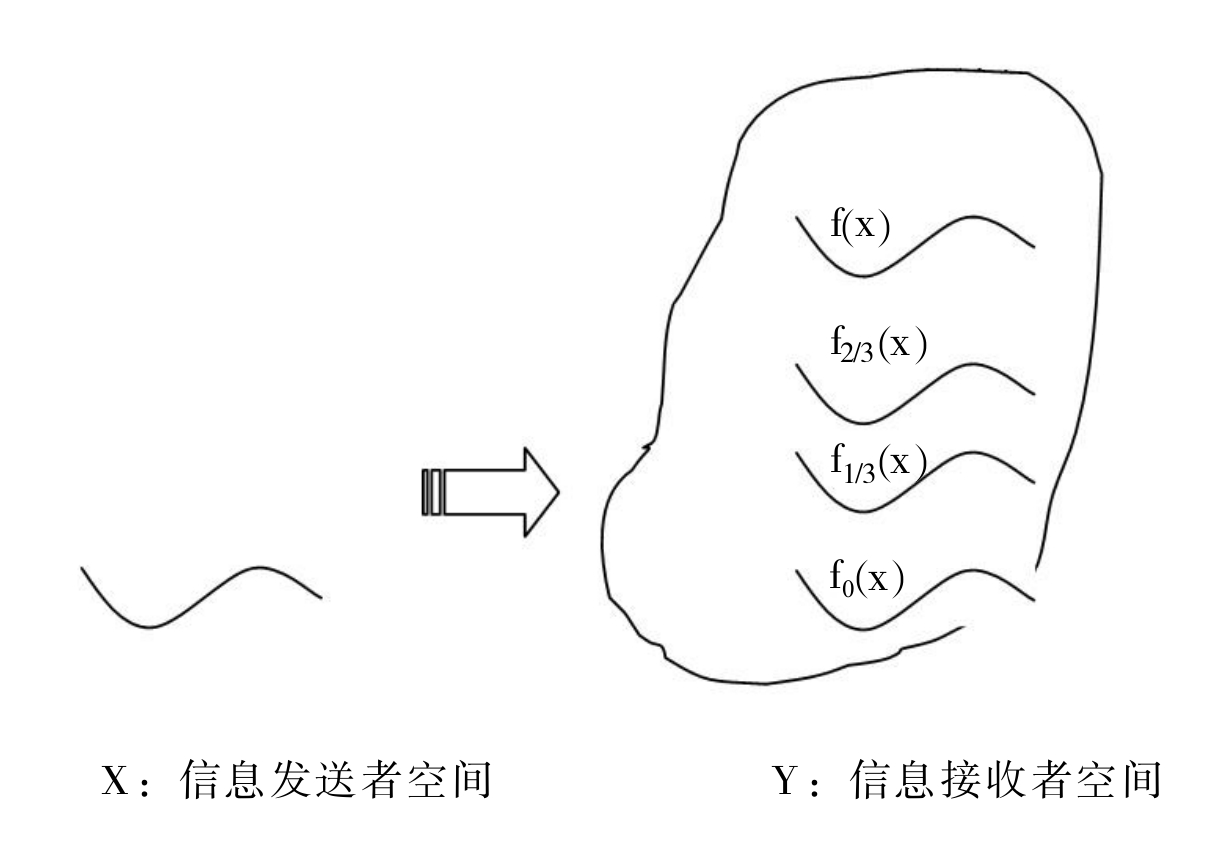
图-2　渠道同伦示意图

定理1　设X和Y分别是信息发送者和信息接收者构成的两个拓扑空间，M（X，Y）是从X到Y的所有信息传播渠道的集合。则在集合M（X，Y）中，同伦关系是一种等价关系。

证明：为证渠道同伦关系是一种等价关系，就是要证同伦关系满足自反性、对称性和传递性。

（1）根据信息传播渠道同伦的定义，设f，g：X→Y是两个连续的映射，则存在连续映射F（x，t）：X×I→Y，满足F （x，0）＝f，F（x，1）＝g。令F（x，t）＝f（x），x∈X，t∈I，显然满足F（x，0）=f，F（x，t）=f，亦即F：f≌f：X×I→Y。即渠道同伦关系是自反的。

（2）设渠道f与g同伦，即f≌g：X→Y，则有F：X×I→Y使得F：f≌g：X→Y，定义F：X×I→Y为F（x，t）＝F （x，1-t），x∈X，t∈I，就知F：g≌f：X→Y。即渠道同伦关系是对称的。

（3）设渠道f与g同伦，g与h同伦，即f≌g：X→Y，g≌h：X→Y，则有F：X×I→Y和G：X×I→Y使得F：f≌g：X→Y和G：g≌f：X→Y。定义H：X×I→Y为

由粘接定理，H为连续映射，并且对所有的x∈X

H（x，0）＝F（x，0）＝f（x）

H（x，1）＝G（x，1）＝h（x）

由此H：f≌g：X→Y。因此，渠道同伦关系是传递的。所以，渠道同伦关系是等价关系。证毕。

渠道的同伦关系是一种等价关系，这一结论具有重要的传播学价值。据此，我们可以把从X到Y的渠道集合分成许多等价类，每个等价类称为一个渠道同伦类。在只有单一信息发送者a和信息接收者b的情况下，这一结论的含义就是我们可以把a与b之间的所有信息传播渠道分成若干渠道等价类。属于同一等价类的渠道具有相同的传播特点，从传播学意义上讲，可以认为它们是没有区别的。属于不同等价类的渠道具有不同的特点，因此，必须区别对待。

现在，我们来讨论渠道的乘积和复合，我们首先给出渠道乘积的定义。

定义3（渠道乘积）设α，β：I→X是X中的两条信息传播渠道，符号α（1）＝β（0），

根据粘接定理，α*β是X中的一条信息传播渠道。我们称α*β为渠道α与渠道β的乘积（如图3所示）

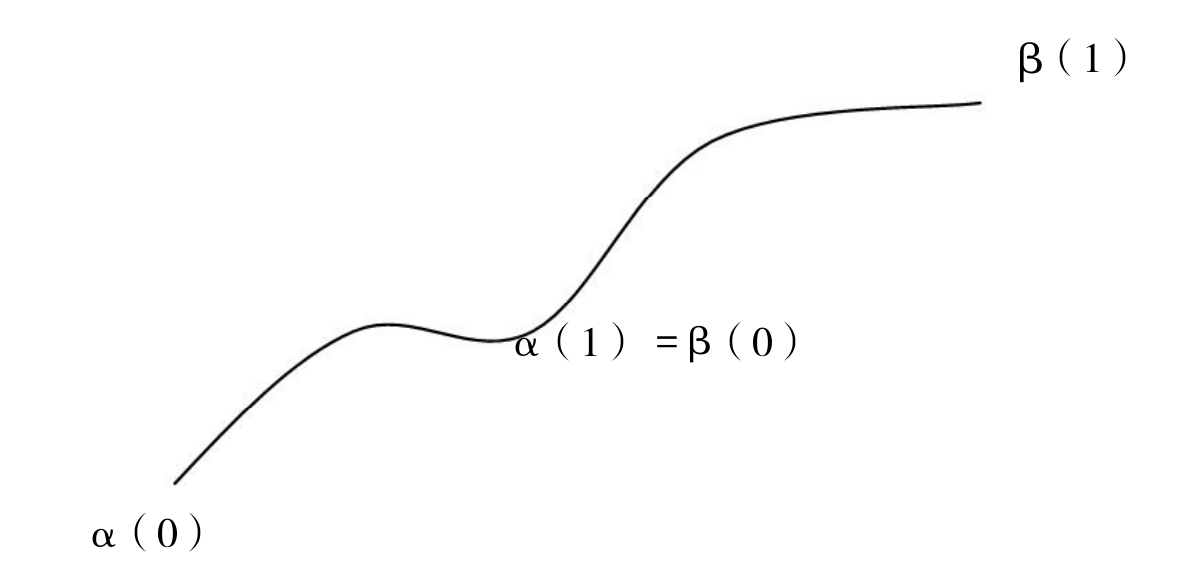
图-3　渠道乘积示意图

由上面的定义不难看出，渠道乘积相当于把两个渠道首尾相接地串联起来，前一半时间用两倍的速度走完渠道α，后一半时间用两倍的速度走完渠道β。因些，只有当α（1）＝β（0）时渠道乘积才有意义。其传播学的直观含义就是信息的接力棒式的传播。

关于渠道复合，我们有如下一般性定理。

定理2 设f0≌f1：X→Y，g⁰≌g¹：Y→Z，则g⁰○f0≌g¹○f1：X→Z。

证明：设F：f0≌f1：X→Y，G：g0≌g¹：Y→Z，

H：X×I→Z

为我们定义

H（x，t）＝G（F（x，t），t）x∈X，t∈I

则有：

H（x，0）＝G（F（x，0），0）＝g⁰（f0（x））＝g⁰of0

H（x，1）＝G（F（x，1），0）＝g¹（f1（x））＝g¹of0

所以，H：g⁰of0≌g¹of1。证毕。

这个定理使我们在处理渠道复合时，可以将若干因子渠道换成与之同伦的渠道，其结果仍得与原来的渠道复合同伦的渠道复合。

三、传播空间与舆论的形成

前面我们讨论了渠道之间的同伦关系，它首先取决于所讨论的连续映射，同时还先决地受到赖以建立渠道的传播空间的制约。这里的传播空间是指以信息接收者集合为基础所构成的拓扑空间。

如果传播空间Y是单点空间或欧氏空间的凸集，则从任意拓扑空间X到传播空间Y的任意两条渠道都是同伦的。也就是说，设V是n维欧氏空间Rn 中的一个凸集，设X是一个拓扑空间（信息发送者空间），f0，f1：X→V是从X到V的信息两条渠道，我们都有渠道f0同伦于渠道f1，即f0≌f1：X→V。事实上，对每一点x∈X，连结f0（x）和f1（x）的直线段整个位于V内。对于每一点x∈X，让f0（x）沿着上述直线段匀速地滑到f1（x），整体上我们就得到一个从渠道f0到渠道f1的同伦。具体说来，我们可以定义映射F：X×I→V为F（x，t）＝（1－t）f0（x）+ tf1（x），x∈X ，t∈I

显然，F是连续的，并且有F（x，0）＝f0（x），F（x，1）＝f1（x），x∈X。所以渠道f0与渠道f1同伦，即F：f0≌f1：X →V。

下面，我们较为详细地讨论一下传播空间的一些特点与舆论形成机制问题。

定义4 设X和Y是两个不同的传播拓扑空间。若存在连续映射。f：X→Y和g：Y→X，满足gof＝1 X：X→X和fog＝ 1Y：Y→Y，我们就说传播空间X和Y具有相同的伦型，记为f：X ≌Y。这时称f为从传播空间X到传播空间Y的一个同伦等价，同时称g为f的同伦逆。

与证明渠道同伦关系是一种等价关系相类似，容易证明，传播拓扑空间之间的同伦关系也是一种等价关系。据此，我们可以根据传播空间的伦型对不同的传播空间进行分类。伦型相同的传播空间所具有的性质称为伦型不变性。传播空间的伦型不变性是传播学所要研究的具有共性的问题。与此同时，伦型不同的传播空间又各具特点，我们必须分类对待。认识到这一点，对我们加深对信息传播过程和信息传递规律的认识具有重要的帮助作用。一般认为，在传播空间中，当持某种观点的成员数n大于某个临界值nc=N时，即认为舆论就形成了，这是“相对舆论”的定义。本文采用“绝对舆论”的定义，“绝对舆论”是指传播空间中的所有成员都持有相同的观点。在以下的讨论中，我们用传播空间X的成员x代表x的观点。

定义5 设X是一个传播空间，x0是X中的任一点。若X上的恒同映射1 X：X→X同伦于把X的每一点都送到x0的常值映射e x0：X→X，我们就说传播空间X是可形成舆论的，或者说传播空间X是可压缩的。

下述定理给出了形成舆论的充分必要条件。

定理2传播空间X可形成舆论的充要条件是，传播空间X与单点空间具有相同的伦型。

证明 先证必要性。设传播空间X可形成舆论, 即有x⁰∈X使得1 X≌e x⁰：X→X，其中e是满足e（X）＝｛x⁰｝的常值映射。按对任意x∈X，f（x）＝x⁰ 定义f：X→｛x⁰｝，按g （x⁰）定义g｛x⁰｝→X，则f与g均为连续映射。同时不难验证

gof＝goe x⁰= e x⁰≌1 X：X→X

fof＝1{ x⁰}≌{ x⁰}→{ x⁰}

所以， X≌{ x⁰}，{ x⁰}是一个单点空间，必要性得证。

再证充分性。

设传播空间X与单点空间具有相同的伦型，即存在连续映射f：X→｛y⁰｝和g：｛y⁰｝→X，使得gof≌1 X：X→X，fog≌1｛y⁰｝：｛y⁰｝→｛y⁰｝

设g（y⁰）＝x⁰，对所有x∈X取e（X）＝x⁰得到常值映射e：X→X，于是

e＝gof≌1 X：X→X

即传播空间X可形成舆论。证毕。

在一般的情况下，传播空间X并不能形成一个共同的“舆论点”，用拓扑空间的术语来讲就是传播空间X不能收缩到X的某一点，但却可以连续地形变收缩为传播空间X的真子空间G而不变动G中的点。在这种情况下，我们就称传播空间X可以形成一个“舆论区域”。

定义6 设G是传播空间X的一个真子空间，若有连续映射F：X×I→X，使得对所有x∈X，H （x，0）＝x，H （x，1）∈G

而对所有x∈G

H （x，1）＝x

我们就称传播空间X是可形成“舆论区域”的，H是X到A上的一个“舆论收缩”，同时称G为传播空间X的一个“舆论收缩核”

如果把上述定义中的条件对“所有x∈G，H （x，1）＝x”改为对所有的x∈G和t∈I都有H （x，t）＝x，我们就称H是X到G上的“强舆论收缩”。“舆论收缩”与“强舆论收缩”的区别在于：前者G中的点可以变化，后者G中的点始终保持不动。由此，我们引进如下“舆论”与“舆论核”的概念。

定义7 设G是传播空间X的真子空间，若存在X到G上的一个连续映射g：X→G，使得对每点x∈G有g（x）＝x，就称f为传播空间X到G上的一个舆论，并且称G为传播空间X的一个“舆论核”。

与信息传播渠道相类似，舆论也是一个映射，而不是映射像，即舆论是f，而不是f（X）。这样我们就用拓扑学方法提出了舆论的一个严格数字定义，这对于传播学和舆论形成机制的研究具有重要的意义。

四、Osgood传播系统的基本群模型

在传播学中，最基本的传播模式就是Shannon传播系统。在Shannon传播系统的基础上，发展了许多更加贴近现实更加复杂的传播模式，如奥斯古德（Osgood）模式、施拉姆（Schramm）模式、纽科姆（Newcomb）模式、韦斯特利-麦克莱恩(Westley-Maclean)模式、和格伯纳（Gerbner）模式等。本文利用拓扑学方法，建立了Osgood传播系统的基本群模型，并讨论了Osgood传播系统的一些拓扑性质。

申农传播系统是申农和韦弗为解决工程问题而发展起来的机械传播模式，它没有考虑人类传播的问题。奥斯古德在申农传播模式的基础上，根据他的意义理论（Theory of meaning）和一般心理语言过程（Psycholinguistic processes in genera）提出了在一个个体内同时具有发射和接收功能的模式。在这个模式中，将符号的“意义”列入了研究范围，而在申农传播模式中对信息的定义特地排除了意义。

在申农传播模式中，信源、信宿、发射者和接收者都是相互独立的，这对工程应用问题来讲通常是正确的。但是，人类传播系统的情况要复杂得多，一个个体通常兼具信源和信宿的功能，同时作为发射者和接收者，通过许多反馈机制对自己编码的消息进行解码。人们通常把具有上述特点的传播系统称为Osgood传播系统。

我们用X表示Osgood传播系统，X显然是一个拓扑空间。设x₀∈X是X的一点，表示Osgood传播系统的一个个体，根据Osgood传播系统的特点，它的每一个个体既是发射者，又是接收者，结合昝廷全（2005）的结论，在X中存在始点和终点都在x₀的渠道（连续数学映射），我们称其为X中以x₀为基点的一个环型渠道，简称环道。在一般情况下，以x₀为基点的环型传播渠道可能不止一条，我们把X中以x₀为基点的环型传播渠道的全体记为Ω（X，x₀）。

环型渠道是一种特殊的渠道，因此，昝廷全（2005）关于渠道的讨论对Ω（X，x₀）中的元素全部成立。显然，Ω（X，x₀）中的所有的环道都是端点固定的（即为x₀），因此，Ω（X，x₀）中先决地确定了定端同伦意义上的等价关系。把环道作为渠道按定端同伦等价所划分出来的渠道类称为环道类。将X中以x₀为基点的环道类的全体记为π₁（X，x₀）。根据昝廷全（2005）的结论，以x₀为基点的任意两个环道都可以相乘。因此，昝廷全（2005）引进的渠道乘积α*β：I→X中的运算*是π₁（X，x₀）中的一个运算。

定理1 Osgood传播系统的环道类集合π₁（X，x₀）在运算*的意义上成为一个群，称为Osgood传播系统X的以x₀为基点的基本群。

证明：①显然运算*是可结合的

②π₁（X，x₀）中存在关于运算*的单位元，即将I中所有点映射到x₀的常值映射e所在的环道类

③π₁（X，x₀）中任一元素都有关于运算*的逆元素。即对任一环道α，都存在环道α的逆道α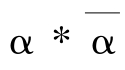，是这样一个渠道：先用一半的时间以两倍的速度走完环道α，后一半时间用两倍的速度逆行回来。

五、 Osgood传播系统基本群之间的同构

前面，在构造Osgood传播系统的基本群时，我们首先要选定Osgood传播系统X中的一点x₀作为基点，并将X的以x₀为基点的基本群记为π（X，x₀）。如果选择Osgood传播系统中的另一点x₁∈X作为基点，我们就将得基本群π₁（X，x₁）。一般来讲，基点的选取可能会影响Osgood传播系统的基本群的结构。这样，随着基点选取的不同，我们就会得出Osgood传播系统不同的基本群π₁（X，x₁），但是，下面的定理2描述了Osgood传播系统的基本群的一个重要性质。

定理2 设X表示Osgood传播空间，x⁰和x¹是X的两个点，ρ：I→X是X中连结x⁰到x¹的一个渠道，则有π₁（X，x⁰） ≌ π（X，x¹）。

证明：如果我们定义映射P：π₁（X，x⁰） →π₁（X，x^1）和映射Q：π₁（X，x¹） →π₁（X，x⁰），同时证明它们都是群的同态，并且QoP=1: π₁（X，x⁰） →π₁（X，x⁰），PoQ=1：π₁（X，x¹） →π₁（X，x¹），则P：π₁（X，x⁰）→π₁（X，x¹）就是一个同构，即有π₁（X，x⁰） ≌π₁（X，x¹）。

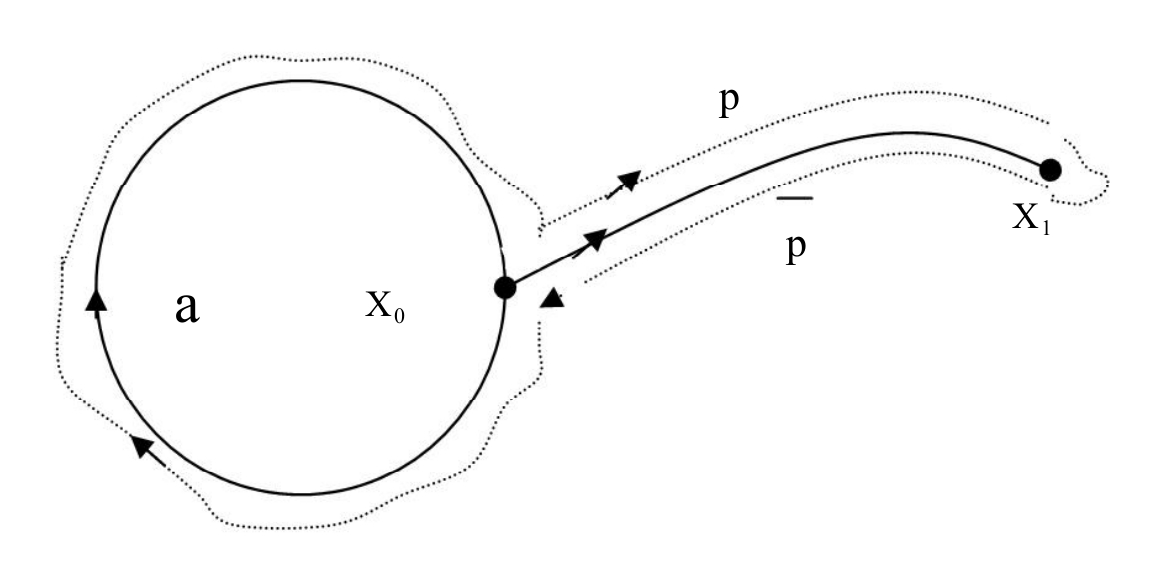
图-4　映射P（·）示意图

现在我们开始证明，定义映射P：π₁（X，x0） →π₁（X，x¹）为

由图-4不难看出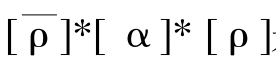，是Osgood传播系统中以x¹为基点的环道，故有P（π₁（X，x0）） ∈π₁（X，x¹）

设[ α]，[ β]为Osgood传播系统中以x0为基点的两个不同环道类，

有

[ α]、[ β] ∈π₁（X，x⁰）

则按定义

故P：π1（X，x⁰）→π₁（X，x¹）是一个同态。

同理可证，如果定义映射Q：π₁（X，x¹） →π₁（X，x⁰）为

则：Q：π₁（X，x¹） →π₁（X，x⁰）也是一个同态。

对于任一[ α] ∈π₁（X，x⁰），容易验证

于是QoP＝1：π₁（X，x⁰） →π₁（X，x⁰）。

同理PoQ＝1：π₁（X，x¹） →π₁（X，x¹）。

综上所述，P：π₁（X，x⁰） →π₁（X，x¹）是一个同构，即有π₁（X，x⁰） ≌π₁（X，x¹）。

根据定理2分别以Osgood传播空间中的两个点x₀ 和x₁为基点的两个不同环道类的集合之间的同构关系完全由x0 与x¹之间的渠道ρ确定，我们不妨将其记作：ρ^＃。

根据定理2，如果Osgood传播系统属于连通的拓扑空间，则对任意的x⁰∈X和x¹∈X，都有：

π₁（X，x⁰）≌π₁（X，x⁰）。

在这种情况下，如果我们只对Osgood传播系统的基本群感兴趣时，常以π₁（X，x）记它的基本群，而不标明以哪一点为基点，因为以X的任何一点为基点所得到的基本群都是同构的，从代数结构的角度来讲都是没有差别的。

现在，我们简要讨论一下Osgood传播系统基本群平凡的渠道连通空间（称为单连通空间）的情况。按照Osgood传播系统基本群的几何含义，单连通空间是这样一种渠道连通空间，它的每一条环道都可以在该空间中连续地收缩成一条常值渠道。只有一个发射者和接收者的传播空间，Rⁿ及Rⁿ中的凸集，都是单连通空间的典型例子。按照任一条环道 都可以收缩为一条常值渠道的直观说法，不难证明，当n≥2时，n维球面是单连通空间，但与欧氏空间中的凸集不同，Sⁿ属于不可形成舆论的传播系统，而Rⁿ中的凸集是可形成舆论的可缩空间。

单连通空间与可缩空间的区别在于，前者可以连续地收缩成一个常值映射，后者可以收缩为其中的一个点或一个子集。关于单连通空间，我们有如下定理。

定理3 设Osgood传播系统X是单连通的，则X中任意两条起点和终点分别相同的渠道都是定端同伦的。

证明：设α、β：I→X是Osgood传播系统中的两个渠道，

α（0）＝β（0）＝x⁰，α（1）＝β（1）＝x¹，则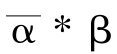：I→X是以x¹为基点的一条环道。由于X单通道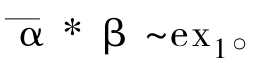，另外，当然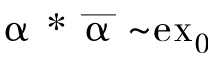，。因此，

六、 Osgood传播系统基本群的伦型不变性

现在，我们转而讨论Osgood传播系统的伦型不变性。首先讨论不同的Osgood传播系统之间的连续映射对相应的环道的作用和对相应的基本群的作用。

定义1 设X和Y是两个不同的Osgood传播系统，x⁰∈X，f：X→Y是一个连续映射。若α和β是X中的以x⁰为基点的两条等价的环道，则显然地foα和foβ是Y中以f（x⁰）为基点的两条等价的信息环道。于是，可以定义

f_＃：π₁（X，x⁰）→π₁（Y，f（x⁰））为

f_＃（[α]）=[foα]。

容易验证，设[α]，[β] ∈π₁（X，x⁰），则f_＃（[α]*[ β]）= f_＃（[α]）* f_＃( [β]），由此知，f_＃π₁（X，x⁰）→π₁（Y，f （x⁰））是一个同态，称为连续映射f的诱导同态。

定理4 设X、Y、Z是三个不同的Osgood传播系统，x⁰ ∈X，则有：

（1） 若f：X→Y和g：Y →Z都是连续映射，则

（gof）_#= g#of#：π₁（X，x⁰）→π₁（Z，g（f（x⁰）））

（2） 若f≌h：X→Y并且F：f≌h，则

h#=ρ^#of_#：π₁（X，x⁰）→π₁（Y，h（x⁰⁾），

其中ρ^# ：π₁（Y，f（x⁰））→π₁（Y，h（x^0））是按ρ（s）＝F（x⁰ ，s）定义的从f（x⁰）到h（x⁰）的渠道ρ：I→Y确定的同构ρ# ：π₁（Y，f（x⁰））→π₁（Y，h（x⁰））。

证明：（1）设[α]←π₁（X，x⁰），则

（gof）_# （[α]）=[ gofoα]= g# （foα）= g#（f#（[α]））＝（g# of#）（[α]）

即（gof）＝g# of#

（2）设[α] ∈π₁（X，x⁰）。根据题设有F：X×I→Y使得F（x，0）＝f（x），

F（x，1）＝h（x），x∈X，

要证h#（[α]）＝（ρ^# of#）（[α]），就是要证

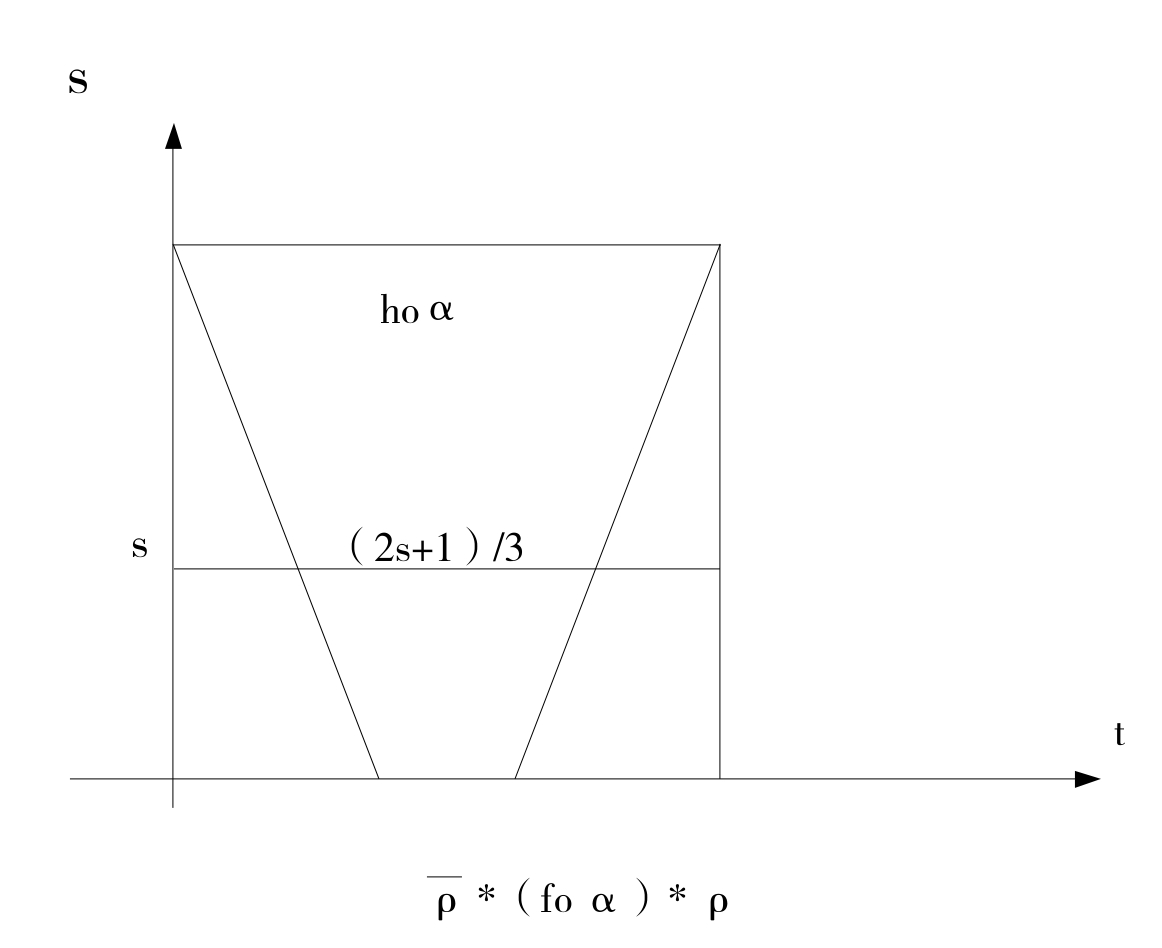
图-5

参照图-5，在左边的三角形，让g_s（t）=G（ t，s）定义的传播渠道g_s：I→Y以三倍的速度沿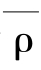走，但走到（1－s）/3为止；在右边的三角形，让g_s以三倍的速度沿ρ走，但从t=（s+2）/ 3开始；在中间利用同伦F从foα变到hoα。注意参数s的水平线与中间部分之交的长为（2s+1）/3，（t-(1-s）/3）*（3/（2s+1））=（3t+s-1）/（2s+1），我们得到所需的定端同伦G：I×I→Y的表达式为：

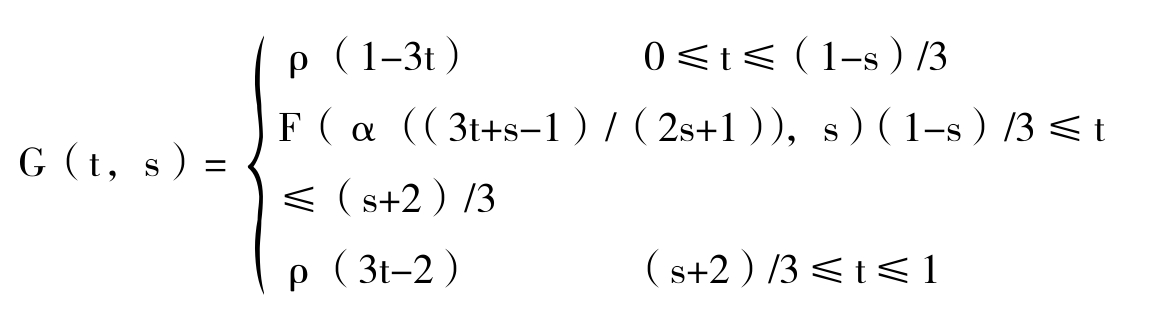
根据粘接定理，G（t，s）是连续映射，并且

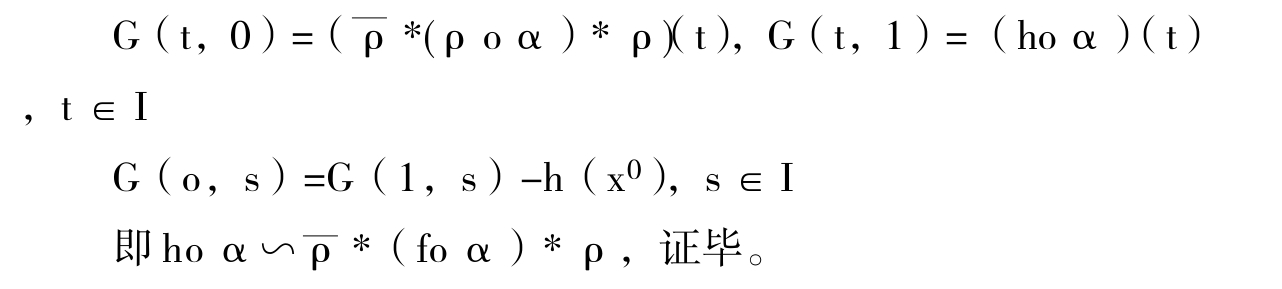
下面，我们就来证明Osgood传播系统基本群的伦型不变性。

定理5 设X和Y是两个具有相同伦型的渠道连通的Osgood传播系统，则有π₁（X）≌π₁（Y）

证明：据题设X≌Y，有连续映射f:X→Y和g：Y→Z，

使得gof≌1：X→Z， fog≌1：Y→Y

任取一点y0∈Y，记x0 =g（y0），则我们有连续映射诱导的同态

f_＃：π₁（X，x⁰）→π₁（Y，f（x⁰））

g_＃：π₁（Y，f（x⁰））→π₁（X，g（f（x⁰）））

根据定理4，有

g#of#＝（gof）#＝ρ^# o1_＃＝ρ^#：π₁（X，x⁰）→π₁（X，g （f（x0）））

其中ρ^#是定理4由gof到1的伦移确定的同构。由此可见，

f_＃：π₁（X，x⁰）→π₁（Y，f（x⁰））是单同态。

同理有

f_# o g_#＝（fog）＝η^＃o1_＃＝η^＃：π₁（x，y ⁰）→π₁（Y，f（x0））

其中，η^＃是定理4中由fog到1的伦移所确定的同构。由此可见，

f_#：π₁（X，x⁰）→π₁（Y， f（x⁰））是满同态。于是

f_#：π₁（X，x⁰）≌π₁（Y， f（x⁰）），证毕。

根据定理5，我们不难得出如下两点推论。

推论1 Osgood传播系统的基本群是拓扑不变量，即同胚的渠道连通的Osgood传播系统的基本群同构。

推论2 可形成舆论的Osgood传播系统是单连通的。

关于可形成舆论的Osgood传播系统，我们还有如下进一步的定理。

定理6 设A是Osgood传播系统X的强舆论收缩核，x⁰∈X，则有

π₁（X，x⁰）≌π₁（A， x⁰）

证明：设H：X×I→X是Osgood传播系统到A上面的强舆论收缩核，则若α是X中以x⁰为基点的环道，γoα就是A中以x⁰为基点的环道，这里γ：Z→A是γ（x）＝H（x，1）确定的从X到A的一个收缩。按照

p（[α]）＝[γoα]， [α] ∈π₁（X，x⁰）

定义映射p：π₁（X，x⁰）→π₁（A，x⁰），容易证明，

p：π₁（X，x⁰）≌π₁（A，x⁰）

最后，我们简单讨论一下Osgood传播系统基本群推广到高维情况所得到的高维同伦的概念及有关结论。

通常称Iⁿ={（x₁，x₂…，x_n）∈Rⁿ：0≤x₁，x₂，…，x_n≤1}为n维欧氏空间Rⁿ中的单位高体，其边界记作：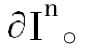

定义2 设X为一个Osgood传播系统，x0∈X，n为正整数，称连续映射

α：Iⁿ→X为X中以x0基点的一个n 维环道，如果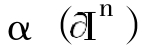＝｛x⁰｝。X中所有以x0为基点 的n维环道的集合记为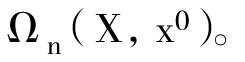在集合Ω_n（X，x⁰）中，定义定端同伦关系如下：

设α，β∈Ω_n（X，x⁰），若存在一个映射H：Iⁿ×I→X，使所有（t₁，t₂…，tn）∈Zⁿ都有

H（t₁，t₂，…，t_n，0）＝α（t₁，t₂，…，t_n）

H（t₁，t₂，…，t_n，1）＝β（t₁，t₂，…，t_n）

而对所有（t₁，t₂，…，t_n，1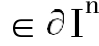），s∈I，都有

H（t₁，t₂，…，t_n，s）＝x⁰

就说点α和β是定端同伦的，记作α~β。

显然，定端同伦关系是Ω_n（X，x⁰）中的一个等价关系，按照这个等价关系可以对Osgood传播系统X中以x0为基点的环道进行分类，称为X中的以x0为基点的n维环道类。α所在的n维环道类记作[α]。Osgood传播系统X中所有以x0为基点的n维环道类的全体记作：π_n（X，x⁰），即：

π_n（X，x⁰）＝Ω_n（X，x⁰）/~这里“~”表示等价关系。

在Ω_n（X，x⁰）中定义运算“*”如下：

设α，β∈Ω_n （t₁，t₂，…，t_n），令α*β：Iⁿ→X为

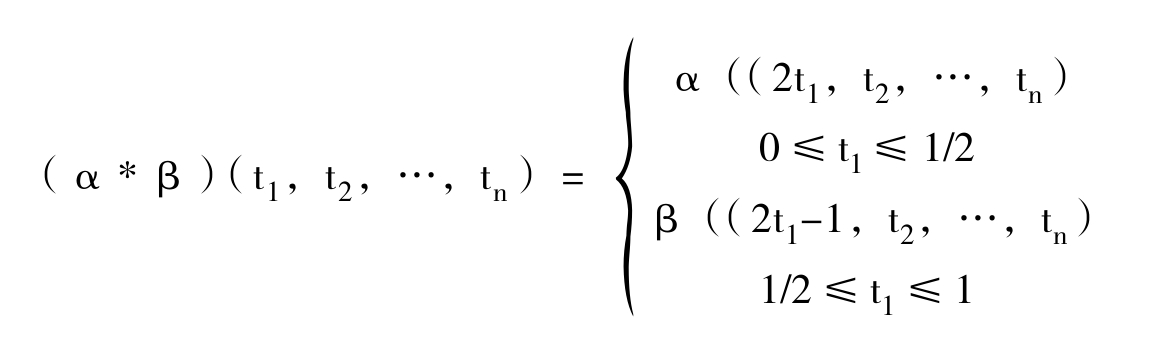
显然，α*β∈Ω_n （X，x⁰），容易验证Ω_n（X，x⁰）上的运算“*”按照[α]△ [ β]= [α* β] 的定义诱导出集合π_n（X，x⁰）上的△运算是可结合的、有单位元的和可求逆的，即π_n在运算△之下成为一个群，称为Osgood传播系统X的以x0为基点的n维同伦群。

七、 讨论与展望

本文是应用拓扑方法研究信息传播过程的一个初步探讨，只是从形式上把传播学和拓扑学联系了起来，所得到的结论还很初步，许多丰富的内涵没有展开讨论，这也是我们今后在这方面研究的一个努力方向。

通过本文的研究，把一类非常典型的传播系统即Osgood传播系统与一个代数系统联系了起来。由于Osgood传播系统的最大特点就是每个个体既是发射者又是接收者，我们自然地想到了代数系统中基本群的概念。

本文建立了Osgood传播系统的基本群模型，详细论述了Osgood传播系统基本群的拓扑特征，给出了相应的定义和定理。关于这些定义和定理的传播学意义还有待于进一步研究和认识。我们真诚地希望有更多的传播学者参与这一研究，使传播学的这一研究方向早日成熟起来。

Primary Research on Topological Communication

Abstract: In this paper, a info communication channel is defined as a strict mathematical mapping by the way of topology. homotopy relations between different communication channels and between different communication spaces are discussed. It is proved that both channel homotopy and communication space homotopy is equivalence relation. Accordingly, equivalence clustering for different communication channels and different communication spaces is made. At last the characteristics of communication space which may form “consensus point” and “consensus area” are discussed in details, a strict mathematical definition of “consensus” is given and it is given that consensus is a mathematical mapping , the sufficient and necessary conditions of consensus formation is proposed. This paper provides a foundation for topological communication study.

What’s more，Osgood communication system is firstly regarded as a topological space, on this basis, a basic group model of Osgood communication system is constructed. The topological characters of Osgood communication system are discussed in details and two inferences are drew : one is that the basic group of Osgood communication system is a topological invariable, the other is that Osgood communication system which can form consensus is singly connectivity

Key Words: communication space　topology　 homotopy consensus Osgood communication system　basic group

参考文献：

C.Shannon and W.Weaver, The Mathematical Theory of Communication, Urbana: University of Illinonis Press, 1949。

沃纳·赛佛林和小詹姆斯·坦卡德（郭镇之等译）：《传播理论：起源、方法、与应用》，北京：华夏出版社，2000年第一版。

林金坤：《拓扑学基础》，北京：科学出版社，2002。

【注释】

(1)原载《中国传媒大学学报》（自然科学版），2006年第1期。