基于网络资源探究的情景化教学案例——《鸡蛋中的数学》

8.3　基于网络资源探究的情景化教学案例——《鸡蛋中的数学》

1.案例说明

《鸡蛋中的数学》是一个非常著名的基于问题解决学习、协作交流学习以及资源共享学习的情境化学习网站。它由UIUC数学系的Steve Bradlow教授和John Sullivan，NCSA的StuartLevy，以及工程大学的本科生BrianKlamik共同研制。其Standalone版本是Beckman学院的StuartLevy和DanielE.Weber共同研制的。

从1999年6月1日至今，鸡蛋数学的教学方案主要涉及如下主题：

鸡蛋的形状，其中讨论了平面的旋转和在平面中画椭圆的方法：

左右对称与横截面

旋转曲面

用钉子和线画椭圆

椭圆中的等量关系

笛卡儿曲线

卡西尼曲线

蛋白和蛋黄定理（也就是通常所说的三明治定理），展示了如何平分位于同一平面的两个封闭区域：

平分蛋白和蛋黄（开始页）

蛋白和蛋黄定理实例

Borsuk－Ulam定理

Borsuk－Ulam定理证明

球面几何，在这个部分中，对球体的曲率做了证明

胚胎中的微积分

理解指数级增长（开始页）

切线和斜率

自然指数e

除了上述主题以外，随着时间的推移，该网站还将增加一些新主题。

2.案例分析

在“鸡蛋中的数学”网站，里面有很多的Java程序供学习者操作，自己动手操作模拟再现、思考总结多个数学公式的产生和论证。该案例利用网页丰富的超链接特性将许多数学问题贯穿起来，用大家熟知的鸡蛋作为问题情境的引入。其主要思想是在鸡蛋里包含了不同层次的数学问题，从中学学习的抛物线到大学里研究的笛卡儿曲线，这是一个学科内不同程度知识的整合，纵向跨度较大。以下展示了其中的一页网页。

附：《鸡蛋数学》网页第一页

细胞的分裂

小鸡孵化的过程究竟有多快？我们知道，任何胚胎的成长过程都是一个细胞不断分裂的过程。从1个细胞分裂为2个细胞，再由2个分裂成4个，然后不断地继续。在此，我们不妨用一个正方形代表鸡蛋的原始细胞，并用图解的方法来阐明这一过程。

将你的光标移入正方形使“鸡蛋受精”，并启动细胞分裂的程序。正方形被平分成2块，然后4块，然后8块，如此继续。这正是一个真实的胚胎中细胞分裂的方式。在正方形的左面，我们以细胞分裂发生的次数为X轴，以每次细胞分裂所得到的细胞数为Y轴作图。你会注意到细胞增长的速度是很快的，如图8－1所示。

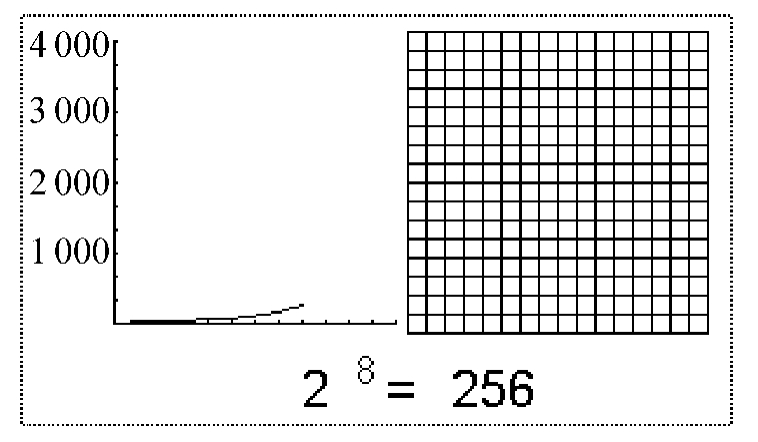
图8－1　一个动态的图示

指数的功能

如果我们使用一些数学的符号，就能够非常有效地对细胞分裂的方法进行描述。让我们将细胞分裂发生的次数表示为字母t，将细胞的总数表示为N（t）。那么，N（1）就表示细胞分裂1次所得到的细胞数，所以，N（1）＝2，与此类似，N（2）＝2×2＝4，N（3）＝2×2×2＝8，如此继续。对于2×2×2，一种更为简洁的书写方法是2³；2×2×2×2则是2⁴，如此继续。用这种方便的符号，我们可以这样写：

N（1）＝2¹，N（2）＝2²，N（3）＝2³，N（4）＝2⁴.

用这种形式，我们可以写出一个关于N（t）的等式，即N（t）＝2^t在数学语言中，N（t）是一个关于t的指数函数。

在上面正方体旁边的图示中，我们使t＝1，2，3，…。并标出了相应的N（t）的位置。将这些点连接起来，我们就得到了一根光滑的曲线，在这根曲线中，无论t被赋给什么值，我们都能够读取相应的2^t的值。

在指数函数N（t）＝2^t中，数字2是指数的底。我们可以通过改变这个底，得到关于t的其他指数函数。例如，以3为底，我们可以得到指数函数3^t。

在右面的课件中，呈现了一系列指数函数曲线，你可以通过移动位于课件顶端的浮标来改变指数的底（以字母b表示）。

值得注意的是，这个指数函数曲线延伸到了t为负数的区域。当t代表的是鸡蛋细胞分裂的次数时，这部分曲线是没有多大意义的。然而，这在数学上却是有意义的，例如，对于以b为底的指数函数b^t而言，数学上规定：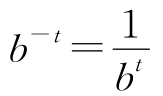

这个规定告诉我们，当t为负值时，如何计算b^t的值。运用这个规定，我们可以进一步推出b^t＋1＝bb^t。

通过多次选择不同的数值给底赋值，你会注意到，所有的指数函数曲线都具有一些共同的特征：

（1）当t＝0时，所有的指数函数曲线都经过同一点。

（2）沿X轴越往左或者右，指数值（曲线的高度）增长得越快；但是越往相反的方向，指数值下降得越慢，而且尽管指数函数曲线越来越接近X轴，但却永远也不会真正地达到它。

值得注意的是，当指数的底b取某些数值时，指数函数值随X值的增大而递增；而当指数的底b取其他一些值时，指数函数则随X值的增大而递减。指数函数的变化趋势取决于指数底的数值。

所有的指数函数都具有第三种更为奇妙的特征。为了理解这个特征，我们需要对这些指数函数曲线的切线加以考虑，尤其需要通过计算这些切线的斜率来考虑其方向。

通过点击，我们可以在某一指数函数曲线上选择一点，经过这点作该曲线的切线。课件底部显示的三个数字分别是：

这一点的指数值，N＝b^t，

经过这一点的切线的斜率（以字母m表示），以及

m/b^t的比值

值得注意的是，随着给出指数函数曲线的不同，前面两个数字将发生变化，但是第三个数字却始终不会发生变化！这就是指数的第三个特征：

（3）切线的斜率与切点的指数函数值成正比。

这个比值（课件中所显示的第三个数字）通常称为比例常数。

一个特殊的底

如果你希望对指数作更为细致的探讨，你将会注意到，上面的那个比例常数是随着指数函数底的变化而变化的。例如，当指数函数的底为2时，这个常数为0.693147，而当指数函数的底为3时，这个常数则为1.0986。

这就使我们不禁要问：当指数函数的底为何值时，能够使比例常数正好为1？这样的底是否存在？

答案是肯定的！这个指数函数的底一般以字母e来表示，也就是说，当指数函数的底为e时，这个指数函数曲线的切线的斜率和这个指数函数的值正好相等。自然指数e具有许多奇妙的特性。你可以通过点击课件上方的e按钮，看到e^t的指数函数曲线及其切线，并对其特征进行观察。

3.案例点评

《数学课程标准》指出：数学教学活动必须建立在学生的认知发展水平和已有的经验基础上。而在传统的课堂教学中，教师很少考虑知识的来源和实际的应用，学生的应用意识淡薄。如何让学生体验到数学与日常生活的密切联系、体会数学的内在价值呢？该案例就是一个好例子。它用学生日常生活中熟悉的鸡蛋作为问题情境的引入，在层层推进的分析中逐步提出新问题，引入新的数学理论。信息技术环境下提供的动画功能使学习材料更为直观，丰富的超链接也能使学生根据自己的情况随时获取相关知识的帮助。以这种生动形象方式引入、介绍数学知识，不仅能激发学生的浓厚兴趣和积极性，由于与生活联系紧密，还能给他们留下深刻的印象，启迪思维，促进他们探索世界的热情。