高中数学新课程探究性学习案例

高中数学新课程探究性学习案例——几何概型

湛江市教育局教研室　陈恒曦

【教学设计及教学实录】

(一)创设情境

师:同学们!我们已经学习了几何概型的有关概念及其在实际问题中的一些应用,今天我们来研究在几何图形中概率问题的计算,先看下面两道例题:

例1　在等腰直角三角形ABC中,在斜边AB上任取一点M,求AM＜AC的概率。

例2　在等腰直角三角形ABC中,过直角顶点C在∠ACB内部任作一条射线CM,与线段AB交于点M,求AM＜AC的概率。

师:上面两道题目是一样的吗？请说明你们的见解.

问题的提出不仅要有探究性,还必须符合学生的认知规律,也就是要具有探究的必要性和可能性,上面两道例题是同一个问题,但背景不同,学生便有了探究的欲望和探究的空间。

(二)学生探究

片刻思考后,发生了以下课堂情景:

生甲:我觉得两道题目是一样的,因为都是同一个三角形同一个条件,而且所要求的概率也是一样,所以只要在AB上取点C′,使AC′=AC(如图1),则所求的概率

图1

生乙:我认为这两道题不一样,刚才的答案只能是例1的结论,如果在刚才的作图中连接CC′,则例2的答案应该是

生甲:不对!怎么可能以角度来代替边长呢？而且同一个问题不可能有两种答案。

生乙:课外书都是这样证明的,怎么可能会错呢？

生丙:现在很多课外书也会出错,如果按乙的方法,我可以以C为圆心,AC为半径作圆弧,然后在刚才作图基础上延长CC′与交于D(如图2),则乙所说的答案实际上就是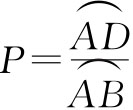。我还可以画另一条任意曲线AEB,并延长CC′与该曲线交于E,那么答案岂不是又变成“P”？显然,这是不能确定的,所以我同意甲的看法。

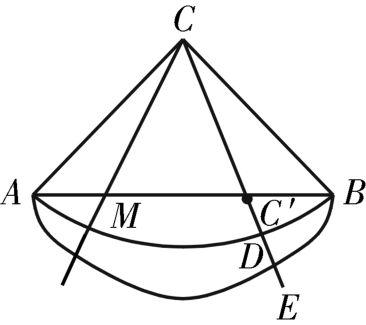
图2

生丁:我不同意丙的说法,你把角度换成曲线是偷换了概念,况且你画的那条奇怪的曲线与点M在AB上出现的对应事件不一定是等可能的。

此时,课堂气氛热闹起来,同学们渐渐分成了两派,争论不休,各自坚持自己的观点。而教师参与其中,并对学生所陈述的观点不时作出适当的评价,大约6分钟后,教师作出解释。

(三)教师指导

师:你们刚才的讨论都非常精辟,令老师也一时难以作出判断。不过有一点请同学们注意,在几何概型中,对于背景相似的问题,由于选取不同的标准来确定等可能事件,所得到的概率是可以不同的。我们不妨再来看下面一个问题:

例3　在半径为1的圆内任意作一条弦,求弦长超过该圆内接等边三角形的边长的概率。

学生先独立探究,然后通过小组交流,再向全班展示不同答案。结果发现,学生的答案基本上囊括了各种结论。教师让学生展示了各小组的其中一部分,例如:

结论1:如图3①,作圆的直径MN,以M为圆心,为半径作弧交MN于D,则当P点落在DN上时,有,故所求的概率为。

图3　①

教师点评:此法还要说明直径MN是任意的或者过M作任一大于的弦等价于MP。

结论2:如图3②,作圆的内接正三角形MAB,则当点N落在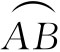上时,有,故所求的概率为。

图3　②

教师点评:此法直观明了,解题思路体现了两个方面的转化:一是“任意作一条弦”转化为同一点M出发的弦；二是把弦长的比转化为弧长的比。这种转化是否正确？同学们可以继续探讨。

结论3:如图3③,作圆的直径MN,分别以M、N作圆内接正三角形,并使正三角形的一边与MN垂直,分别交MN于点P、Q,则当弦AB⊥MN并且与MN的交点在P与Q之间时,有,故所求的概率为。

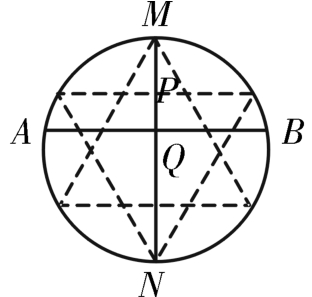
图3　③

教师点评:请同学们判断此法与结论1的异同。

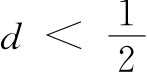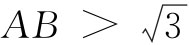结论4:如图3④,在圆内任意作一条弦AB,作出圆心O到AB的距离d,则当时,有,故所求的概率为P=。

图3　④

教师点评:你们对几何概率的理解真是太棒了,简直可以和数学家比美。

(四)课堂小结

师:请同学们想一想,上面这些结论为什么答案都不一样呢？到底哪个是标准答案呢？

生:(小声议论)

师:其实你们今天挑战了一个伟大的问题,这个问题几乎改变了数学的历史。想知道为什么吗？

生:(齐声)想!

师:你们刚才所解答的例3,其实就是历史上著名的贝特朗问题(也称贝特朗概率悖论),贝特朗是法国著名数学家,他在1889年提出了概率悖论:“在圆内任作一条弦,其长度超过该圆内接等边三角形边长的概率是多少？”这个问题提出后,在数学界引起了很大的震动,促使数学家们理性反思概率的基础理论。直到1933年,俄国数学家柯尔莫哥洛夫,创造了概率的公理化定义,从而贝特朗问题才得以解决。

关于“概率的公理化定义”,柯尔莫哥洛夫写在他的经典著作《概率论基础》中,它涉及测度理论,有兴趣的同学,可以在课外去图书馆或上网搜索相关资源作进一步研究。

(五)拓展练习与课后作业(略)

【教学反思】

本节课是在学习了几何概型基本概念及其相关知识的基础上所安排的一节探究课。主要以几何概率中的“悖论”为教学背景,通过知识矛盾创设问题情境,引发学生的探究活动,体现以学生为主体,教师为指导的课程理念,给学生提供一个展现自我的教学平台。

本节课实现三维目标的情况有:(1)知识与技能。通过创设主动学习环境,使学生进一步理解几何概率的实际意义,并能较深刻地领会和熟练掌握处理几何概率问题的一些基本思想和技巧。(2)过程与方法。以例题为载体,将同一个问题放在不同背景中,提出不同角度的要求,引发矛盾与探究,从而总结归纳出求几何概率问题的一般规律和方法,同时培养学生发散思维与创新思维能力。(3)情感、态度与价值观。借助探究活动,提高学生的参与意识和学习兴趣,并养成严谨的科学态度和辨证、客观、全面思考问题的思维习惯,以及正确看待事物的优良品质。

新课程应该怎么教？什么样的课堂才是符合新课程理念的课堂？学生究竟需要什么样的课堂教学活动？作为新课程的直接参与者和实施者来说,不少教师都经历了从“摸着石头过河”到被人说成“穿新鞋走老路”的过程。教师的备课从过去写教案到现在写教学设计,学生的学从过去的被动接受到现在的“自主、合作、探究”,当中究竟改变了什么？如何在课堂上实现新课程所要求的三维目标？这些问题一直都在困扰着广大的一线教师并左右着教师的教学行为。本案例从改变教师角色的角度出发,作了一些尝试,希望新的课堂不再是教师主宰和控制的神坛,而是师生共同探究的舞台。诚然,这种尝试是非常肤浅的,也是很不成熟的,而且还存在着课堂教学容量过低的明显问题,因此只能当作抛砖引玉,提供参考而已。