简单的方程,古怪的结果

许多物理系统呈现对初条件的敏感依赖性;失之毫厘,差之千里。

设有一个一元函数

是区间[0,1]到[0,1]的一个迭代。式中λ是实参数。当f(λ,x n-1)为非线性函数时,这个一维映象描写一个非线性系统,由x的任意初始值,通过上述的迭代过程,可以做出一个确定的过程或时间序列。现在我们从简单的抛物线模型开始讨论,此时

于是

现研究参数λ对迭代带来什么影响。这里,x被限制在0和1之间,而λ被限制在0和4之间。因为当λ>4时,把1/2放进去迭代,得到的值大于1,就不再是[0,1]区间到[0,1]区间的迭代了。

迭代中,主要研究不动点和周期点的情况。该不动点和周期点的值以ξ表示。当f(ξ)=ξ时,ξ就是不动点,也可称之为1周期点;当f(ξ)≠ξ, 但f(f(ξ))=ξ,即迭代两次回到原处时,ξ就是一个2周期点,以下依此类推。

(1)0≤λ≤1。

首先分析0≤λ≤1的情况。一旦λ被给定,在式(2)中λ就是常数。对于式(2)代表的迭代系统,在[0,1]区间内只有一个满足ξ=f(ξ)平衡态或不动点,即ξ=0。按照迭代式(2),不管参数λ是多少,0代进去总是得到0。从数学上来说,就是式(2)将ξ映射为自身。从物理上来看,就是这个平衡态是稳定的,不论x的初值在[0,1]区间内取任何

值,总有x→ξ(=0)。例如,设值的初值取0.5,则迭代结果有

这里,括号内的数表示迭代的次数。从迭代数据看,虽然递降得很缓慢,但最后是趋近于零:x→ξ(=0)。

结论是,当参数0≤λ≤1时,式(2)所表示的迭代系统都只有ξ=0这样一个(贫乏的)不动点。

(2)1<λ≤3。

当参数1<λ≤3时,ξ=0仍然是一个(贫乏的)不动点,但另一个不动点出现了,那就是

很明显,将这个ξ值代入迭代式(2),便有

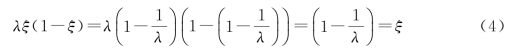
由此可见,只要λ>1,ξ=1-1/λ就是一个不动点。

结论是,在1<λ≤3时,迭代式(2)至少有两个不动点:一个是贫乏的不动点ξ=0,而另一个是ξ=1-1/λ。

下面让我们看看长期迭代的效果。作为一个不动点,一定要考察它是否稳定。从迭代公式来看,ξ=0当然是一个不动点;但是,从一个物理系统或是一个生物系统里得到的数据,一般都是近似值。0不一定精确地等于0,既可能是0.0001,也可能是0.00000001。因此,我们要研究用近似值代替精确值时迭代系统的稳定性问题。

稍加研究,就可发现,当λ>1时,0这个不动点是不稳定的。这就是说,只要和0差一点点,长期迭代下去,就会差得很远。以λ=2为例,用0.0001进行迭代,可以得到:

这里,括号里的数字表示迭代次数。

由此可见,从ξ=0这个不动点旁边一点点开始迭代,很快就跑到别的地方去了。如果从0.00000001或0.000000000001开始,多花一点时间,也是要跑到其他地方去的。这一点跑到哪里去呢?从上面的迭代可以看出,当λ=2时,这一点跑到0.5000的地方了,因为1-1/λ=1-0.5=0.5。这0.5恰恰是另一个不动点。所以,我们说,当λ=2时,ξ=0这个不动点是不稳定的;而ξ=1-1/λ=0.5这个不动点是稳定的,是系统的平衡态。事实上,对所有λ>1的情况而言,ξ=0这个不动点都是不稳定的。

上述的计算过程,实际上可以用作图法对抛物线方程 (2)进行迭代。如图1所示,设纵坐标记xn,横坐标记xn-1,只需考虑第一象限的抛物线,注意45°的角分线。取初始值x0=0.1,或其他值,只要它介于0和1之间。上述迭代过程得到序列x0,x1,x2,x3,x4,…。从几何角度看,不需要做具体计算,便可以一步一步画出迭代过程。首先由初始点 (x0,0)做纵轴平行线,找到与抛物线的交点A(x0,x1)。A的纵坐标就是x1。由点A(x0,x1)做水平直线,求它与45°线的交点B(x1,x1)。经B点再做纵轴的平行线,求得与抛物线的交点C(x1,x2)。这样,就得到x2了。以下依此类推。图2示出了y=xn=λxn-1(1-xn-1)的迭代过程。当λ=2.7时,迭代收敛到稳定的不动点。

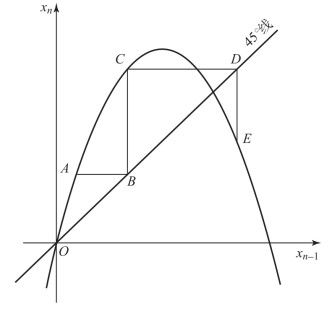
图1　作图法迭代过程示例

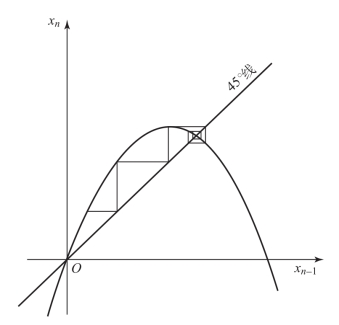
图2　λ=2.7时迭代收敛到稳定的不动点

(3)3<λ≤1+。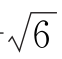

当参数λ再增大时,人们发现,如果λ>3,ξ=1-1/λ这个不动点也变得不稳定了。例如,取λ=3,ξ=1-1/λ=0.7是一个不动点,但只

要有一点点误差,比方说用0.669去迭代,就会跑到别的地方去。迭代情况如下:

由此迭代可见,由0.669开始,迭代既不收敛于0.7这个不动点,也不靠近原来的出发点0.669,而是一会儿为0.83027,一会儿为0.469 72,就在0.83027和0.469 72这两个周期点之间来回游动。由这个迭代试验可见,当λ=3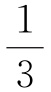时,不动点ξ=0和ξ=1-1/λ=0.7都是不稳定的;相反, 2周期点0.83027和0.469 72是稳定的。

同样,当λ=3.2时,两个稳定的2周期点的解是0.799 45和0.51304。

试验表明,当λ取3到1+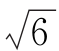(=3.449 489 743)之间的值,即3< λ≤1+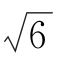时,对于任意的初值x,在迭代次数趋于无穷大时,序列无限趋近于ξ1→ξ2→ξ1→ξ2,即ξ1⇔ξ2。这是式(2)的一个周期2解。同样,我们可以用作图法求出ξ1,ξ2的2周期解,如图3所示。由此可见,以式(2)表示的动力学系统,在它的参数λ跨越λ1=3这个值时,系统的稳定解由周期1变为周期2解。就是说,系统的稳定解经历了一个1分为2的分岔过程,如图4所示。

图3　抛物线迭代出现2周期点

图4　稳定周期点的轨迹发生分岔(3<λ≤1+6)

(4)1+<λ<3.569 945 672。

现在,让参数λ再增大,就可以知道,当λ>1+(=3.449 489 743)时,2周期解也变得不稳定了,情况和参数增大到λ>3时1周期解变得不稳定一样。这时,取而代之的是稳定的4周期解。系统的运动又经历了一个2分为4的分岔过程。λ2=1+(=3.449 489 743)是系统2分为4分岔过程的分岔点。

我们继续讨论下去,随着参数λ值的继续增加,系统就会依次出现8周期解、16周期解等稳定解和相应的分岔过程……当λ增大到λm时,周期2m-1的稳定解分岔为2m个周期2m的稳定解,如此继续下去。这就是著名的周期倍增分岔现象。现将分岔情况和相应的分岔点λ的值列举如表1所示。

表1　周期倍增分岔情况与分岔值λm以及菲根鲍姆常数δ

由此可见,分岔由1分为2,2分为4,直到无穷,此时λ取极限值:λ∞=3.569 945 672。经过不断分岔,系统是一个周期2∞的稳定解。当λ值超越上述极限值λ∞时,式(2)表示的系统即进入混沌。也就是说,从λ∞到4这一段,迭代系统就出现混沌现象。

图5给出了周期倍增分岔导向混沌的示意图。可见,周期倍增分岔,越分越密,密得不得了的时候,就糊成一片,出现混沌。实际考察一下从周期到混沌的机制,很明显,周期倍增,越来越大,当周期数大得无穷大时,已无周期可言,迭代的数据到处乱跑,无法把握,出现混沌现象。这一结果也可以用与时间序列相应的频谱图表示。随着参数λ值的增加,应该先看到离散谱,而混沌区则是连续谱,如图6所示。

美国物理学家菲根鲍姆(M.Feigenbaum)发现,在周期倍增分岔过程中,随着分岔次数m的增加,相邻两个分岔点λm-1,λm,λm+1的间距组成一个等比数列,其分岔宽度εm,εm+1,也组成一个等比数列。在参数λm序列收敛的过程中,这两个等比数列都存在一个极限值。菲根鲍姆还测出了这两个等比数列的公比。它们的倒数被分别称为菲根鲍姆常数δ和菲根鲍姆常数α,即

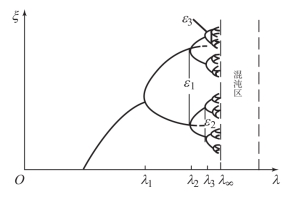
图5　周期倍增分岔导向混沌

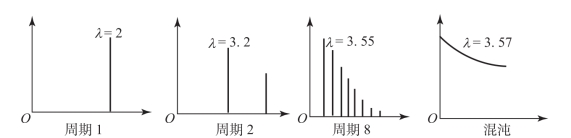
图6　频谱图

已经证明,菲根鲍姆常数δ=4.669 2,与圆周率π及自然对数的底e一样,是一个普适常数,对许多经分岔过程进入混沌的系统都有意义。例如,对于其他函数,如

也会产生周期倍增分岔现象,也有同样的菲根鲍姆常数δ。

周期倍增分岔的一个重要之处在于,当在实验中看到它时,不可能把它误认为是别的什么现象,并且我们还知道在分岔之后的λ∞存在混沌。因此,在流体力学中观测到菲根鲍姆倍增分岔就成为模态不得不向混沌让路的特别令人信服的证据。

就像牛顿力学的建立与万有引力常数G相联系,狭义相对论的建立与光速c这一宇宙常数相联系,量子力学的建立与普朗克常数h相联系,统计物理学理论与玻尔兹曼常数k相联系一样,在混沌理论的研究中,菲根鲍姆常数δ这样一个标志物质运动复杂性问题的常数的发现,将有可能把复杂性的问题纳入某种数学模型中,从而导致混沌理论研究的突破性进展。

(5)λ∞(3.569 945 672)<λ≤4。

现在研究混沌区的结构。此时,式(2)中的参数λ在λ∞=3.569 945 672 和4之间取值。混沌区的结构相当复杂。首先,在这个区间的最边上,即λ=4时,存在周期为任意整数的解,并且全部都是不稳定的。其次,在混沌区存在倒分岔过程,当λ从4逐渐减少到

λ(1)=3.678 573 511

时,混沌区由一片变成两片。随着λ再减少,出现如图7所示的两片分岔为4 片,分岔值为λ(2);当λ取λ(3)时,4片分岔为8片,等等。分岔值的极限为

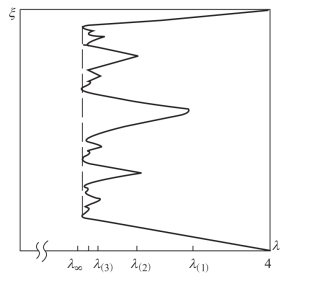
图7　混沌区的倒分岔

当λ取小于λ∞值时,就进入图5所示的分岔过程。它同上述的倒分岔过程一起组成了式(2)中参数λ在0~4取值时,系统出现的分岔和混沌。此外,在混沌区还有一系列的周期窗口。它们是两个周期4窗口,多个周期5窗口、周期6窗口等,在λ=1+=3.828…处有周期3窗口。每个窗口内还有分岔过程,如图8所示。如果将窗口的分岔结构放大,则会得到同样的分岔结构。如此下去,不断地重复整体的图形。图9示出了一维映射x n=λx n-1(1-x n-1)的分岔图。

图8　在λ=1+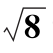=3.828…处周期3窗口的分岔

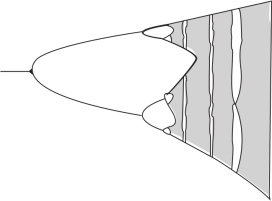
图9　一维映射x n=λx n-1(1-x n-1)的分岔图

以上我们以最简单的抛物线方程为例,说明了一个十分简单的定系数的代数迭代方程。在迭代过程中,得到了从简单到复杂,从规矩到古怪,出现了周期倍增分岔直至混沌的结果。

由此可见,一个系统怎样导致混沌,其基本思想是实现这样的数学回路:系统的输出能够不断地反馈到它自身作为新的输入。这种回路无论是简单,还是复杂,都可出现稳定的行为和混乱的行为。它们的差别仅仅在于系统的某一参数取值的不同。这个参数只要有极小的变化,就会造成回路系统的行为从人们通常熟悉的有序状态平滑地转化为表面上看来是杂乱无章的状态,即逐步地演化为混沌。

以生态学为例,罗伯特·梅(Robert May)1974年从生态学角度研究迭代公式(2)表达某种物种的规模变化规律。这个物种一代一代之间是不交叠的。例如,温带的许多昆虫就是这样,同时孵化,同时成虫,同时变蛹,同时化蛾,同时产卵。这样,当我们说这个物种在某时刻的规模时,所有的个体都是同一代的个体,没有交叠。在这种情况下,我们说该物种的规模是离散的。这时,式(2)中的x n-1,x n分别是该物种第n-1代和n代的密度,λ是常数。现在我们考察经过一代一代的变迁,该物种的变化情形如何。实际上,对这一问题我们在上面已充分研究过。当λ= 1.5时,物种经过一代一代的变迁,物种密度稳定在大约1/3的水平。当λ =2.5时,物种密度稳定在大约0.6的水平。也就是说,当1<λ<3时,物种的密度经过一代一代的发展,总是趋向于一个稳定值。

当3<λ<3.570时,物种密度变化都呈现出周期性质;当λ比3大一点时,周期为2,随着λ的增大,逐渐出现周期为4,8,16,32,…的变化。当λ>3.570时,式(2)的形式依然这么简单,但物种一代一代发展的结果没有表现出什么规律。此时代表物种的一代密度的点仿佛是随机地出现,构成杂乱无章的踪迹。这就是混沌。

混沌(Chaos)又称浑沌,一般指错综复杂、杂乱无章、模糊一团的状态。在这个意义上,它和无序(disorder)的概念是相同的。我国古代学者把混沌描绘为物质未被开化的一种无序的元气状态。他们认为,宇宙的初始状态也是处于天地未形、混混沌沌、动荡不定、明暗不分、阴阳掺和的混沌状态。我国神话把盘古开天地以前的宇宙状况就称为混沌。自然界实际上存在着大量混沌现象,但在牛顿力学创立以后,一种机械的精确决定论的思想得以流行,混沌现象被逐出科学研究的范围。

关于混沌的系统研究起源于20世纪60年代,美国气象学家洛伦茨(E.N.Lorenz)对大气运动的研究。他在计算机上用描述流体热对流的一组简化的确定性方程模拟天气的演变过程。其目的是想利用计算机的高速运算来提高天气预报的准确率。多次模拟的结果表明,初始条件相差甚微,计算结果却大相径庭——得到了非周期性的、混乱的结果。鉴于气候变化的复杂性,输入的初始条件不可能包括所有的细小因素,但这些细小因素能对预报结果产生极大的影响,甚至得出相反的结论。一个确定的含有3个变量的自洽方程,却会导出混沌解。洛伦茨认为混沌是非线性造成的,而混沌来自确定性的规则,是由确定性导致的随机性。所以,从原则上讲,对天气不可能做出精确的预报。特别是长期天气预报,本身就是一个力学方面的混沌现象。洛伦茨用一个形象的比喻来表达他的科学发现:在南半球某地的一只蝴蝶偶然扇动翅膀所带来的微小气流,几星期后可能变成席卷北半球某地的一场龙卷风。这就是著名的“蝴蝶效应”。

实际上,彭加勒在20世纪初早已发现,三体相互作用会陷于混沌。后来,泰肯(F.Takens)等也发现,当系统内有3个以上不同频率的振荡互相耦合时,系统就会形成无穷多个耦合频率的振动,使系统进入混沌。这种混沌状态可被看作无穷个频率耦合的振动现象。但是,混沌(Chaos)一词起源于1975年约克(J.A.Yorke)和李天岩(T.Y.Li)在研究函数的区间迭代时,发现确定性方程中出现周期解和混沌解,并将其命名为“Period Three Implies Chaos”。当时李天岩把此题目汉译为《周期三则乱七八糟》。后来中国学者将它译得较为文雅为《周期三蕴涵着混沌》。从此混沌(Chaos)一词便成为专门术语。李—约克深刻地揭示了混沌的本质特征:混沌动力学系统关于初始条件的敏感性以及由此产生的解的最终性态的不可预测性。混沌被理解为在确定性的动力学系统(指随时间确定性地变化的系统)中的无规行为或内在随机性。这一类确定性的动力学系统通常由微分方程、偏微分方程、差分方程以及简单的代数迭代方程描述,并且这些方程都是定系数的。自然界和经济学界中,有许多现象都可用这一类方程描述。人们还发现,即使原来认为可以用牛顿运动方程精确解决的力学问题,也存在“偶然性”的结果,即根据“精确的”初始值进行的计算,却会得出不确定的多种结果,而且十分敏感地依赖于初始条件。可以这样说,如果一个接近实际而没有系统内在随机性的模型仍然具有貌似随机的行为,就可以称这个真实物理系统是混沌的。

洛伦茨等人的发现,无疑是对传统理论的巨大挑战。在研究客观世界的规律时,人们原先认为只存在两类现象:决定性现象和随机性现象。故物理学中仅有确定论和概率论两套描述体系。描写质点运动方程的牛顿力学直到狭义相对论和广义相对论是确定论描述系统的代表。确定论,指物理世界中严格的因果关系。任何时刻,一个物理系统的情况都是可以完全被确定的,而且以后任何时刻的情况,也可以由那一时刻的情况由物理定律推知。这就是说,描述系统运动的方程一旦确定,只要给定初始条件,就能决定系统的过去和未来。人类由此能预知日食、月食、哈雷彗星回归等天文现象,而且可以预先把这些现象发生的准确时刻算出来,如算出人造卫星的运行轨道等。自牛顿力学起,对事物变化的看法总是被确定论控制。拉普拉斯所说的“没有什么是不确定的”是经典确定论的典型语言。量子力学的不确定性关系,却告诉我们:对于微观粒子,无法同时精确地确定它的位置和速度。这就给了确定论一个小小的打击。

随机性现象出现在一定的宏观条件下,同时又受随机因素的作用,因而人们无法确定其每一次的结果,但能够断言其出现某种结果的概率。分子物理学和热力学,特别是布朗运动,是概率论描述体系的代表。单个气体分子运动的随机现象,表面上看来是不可捉摸的,纯粹是偶然性起作用,但大量分子的集体和总体表现服从一定的统计规律。人们借助概率统计的方法,使分子物理学的计算变成实际可能的计算。

但是人们发现,除了以上两类现象,还存在第三类现象——混沌现象。例如上面我们研究的区间迭代是一个确定性系统。如果在式(2)中送入x n-1,就能算出来x n。x n是一个确定性的变量,而不是“不能准确预知、只能概率估计”的随机变量。可是,这个确定性系统对初值的依赖十分敏感,开始差一点点,后来就不知跑到哪里去了,又变得不可捉摸了,出现了像随机过程一样的不确定的结果。真的随机过程是,下一次结果如何是无法准确预知的。假的随机过程是,只要数据准确,下一次的结果完全是可以预先确定的。只是由于“失之毫厘,谬以千里”,不断迭代的结果,系统才变得不可捉摸。所以,假的随机过程从长期来说是不可预测的过程。

确定论系统的这种假的随机过程,叫作伪随机过程。它不是由于数据的随机性产生的,而是由系统本身的内在随机性产生的。这样的系统运行下去,一定会出现类似随机过程的混沌现象。确定论系统中出现的内在随机性,表明某些系统,不外加任何随机因素,就可能出现与布朗运动不能区分的行为;而其对初值细微变化的敏感依赖性,使得确定论系统的长时间行为必须借助概率论方法来描述。由此可见,在物理学中的确定论描述和概率论描述之间存在由此及彼的桥梁。混沌动力学的发展,正在缩小这两类对立描述体系之间的鸿沟。因此,混沌现象的发现是人类认识继相对论、量子力学以来的又一重大飞跃。

随着对混沌现象研究的深入,人们越来越认识到,这些看上去不可思议的无秩序状态,并不是什么罕见的现象,而是普遍地存在于自然界各个领域之中。混沌现象之所以显得捉摸不定乃是由于它内部蕴含着非线性因素,只要初始条件有些微不同,就可以引起种种大相径庭的结果。因此,简单的数学方程也可能得出复杂的答案。这是对复杂现象必来自复杂系统这一传统观念的挑战。自20世纪70年代以来,人们寻找混沌现象的规律并把混沌动力学用到生物学、医学、湍流理论、电网络理论、结构力学、等离子物理、光学、社会现象、心理现象等领域;一些研究专家把分叉和混沌理论与经典的非线性振动理论相结合,发展成为现代非线性动力学理论,并把它用于工程实际的研究中,如航天工程、先进装备和车辆工程。不少专家认为,混沌理论是解决目前众多复杂疑难问题,如长期天气预报、地震预报、经济预报、涡旋星空、高性能神经计算机等的希望所在。

混沌动力学这门学科非我的这篇短文所能说得清楚的。这里仅是从抛物线方程引出有关混沌动力学的最基本概念,使读者对混沌动力学的科学方法有一个初步的了解。从混沌学的发展来看,多少年来,人们都没有想到,在这样简单近乎幼稚的问题里竟会蕴含着如此深奥的内涵。但科学家们,如洛伦茨(E.N.Lorenz)、约克(J.A.Yorke)、李天岩(T.Y.Li)、罗伯特·梅(Robert May)、菲根鲍姆(M.Feigenbaum)等并没有放过这些貌似幼稚的问题而是追索到底,从而使混沌动力学成为20世纪中继相对论和量子力学后又一个重大发现。这是值得我们每一个从事科学研究的人好好学习和思考并能从中得到启迪的。