-方程的建立

在黏性流体中取一边长为d x,d y,d z的长方体,各表面应力的方向如图5-11所示。以平面ABCD为例,作用在平面上的应力有法向应力p zz与切向应力τzx和τzy。图中各应力的值均为代数值,正值表示应力沿相应坐标轴的正方向,反之亦然。由于流体不能承受拉力,因此p xx,p yy,p zz必为负值。由牛顿第二定律,x方向的运动微分方程如下

图5-11　表面应力示意图

化简后,得这就是以应力表示的黏性流体运动微分方程式。式中ρ对于不可压缩流体是已知常量,通常单位质量力X、Y、Z也是已知量。九个应力和三个速度分量是未知量。式(5-30)中的三个方程加上连续性方程共四个方程,不足以解这十二个未知量,需要补充关系式,使方程组封闭,这些封闭条件就是连续介质力学中所谓的本构方程,即下面所述的应力和变形速度的关系式。

三元流动的牛顿黏性定律及法向应力的理论推导比较复杂,这里仅给出其结论,具体推导可参见相关文献。根据三元流动的牛顿黏性定律,切应力可以写成如下形式

由于两个相互垂直面上的角变形速度相同,所以它们的切应力相等。对于三元流动,法向应力p xx,p yy,p zz可表示为

式(5-31)可以消去式(5-30)中的六个变量,式(5-32)中三个法向应力变换为一个压强函数p,进一步减少了两个变量,这样方程(5-30)的未知数只剩下四个,与方程的个数相等,原则上已可求解了。

在将牛顿流体本构方程应用于建立流动微分方程之前,有必要首先对牛顿流体本构方程本身进行一些讨论,以对前面各章涉及的相关问题或概念作出回应,同时也有助于增进对流动过程中流体变形速率、应力、压力等有关概念的理解。

(1)正应力与线变形率　由牛顿流体本构方程可见,流体正应力由两部分构成:一部分是流体静压力产生的正应力(压应力-p);另一部分是黏性流体运动变形所产生的正应力(拉伸或压缩应力),且仅与流体的线变形速率即有关。其中,如在x方向,流体流动变形产生的正应力包括:,前者反映x方向线应变率的贡献,而后者反映其他方向线应变率的贡献。流体正应力与线变形率相关这一性质,与虎克定律中固体正应力仅与线应变相关是类似的。

如果将黏性流体运动变形所产生的正应力称为附加黏性正应力,或简称为附加正应力,并用Δp xx、Δp yy、Δp zz分别表示x、y、z方向的附加正应力,即

则直角坐标系流场中任一点的正应力p可表示为

(2)附加正应力与流体流动　为进一步阐明附加黏性正应力的物理意义,不妨考察流,故根据式(5-33)有体只沿x方向流动的情况。此时,Δ

由此可见,附加黏性正应力的产生是流体速度沿流动方向的变化所导致的。加速时,所以Δp xx>0;减速时,所以Δp xx<0。物理意义上,因为加速时同方向一前一后两流体质点将处于分离趋势,流体线的变形为拉伸变形,故由此产生的附加黏性正应力为拉应力(正);反之,减速时同方向一前一后两流体质点将处于挤压趋势,流体线的变形为压缩变形,故由此产生的附加黏性正应力为压应力(负)。

如果加速过程中线变形率很大,使得Δp xx=p,则流体将发生分离,失去连续性,故对于连续的真实流体,总有p xx=-p+Δp xx≤0,即不承受拉应力。特别地,如果该流动是等速的,即=0,则必然有Δp xx=0。

(3)正应力与静压力　由p xx=-p+Δp xx可知,流体静止条件下,因Δp xx=0,所以p xx=-p。由此得到一般性结论:静止条件下流体的正应力数值上等于流体静压力p,且为压应力,即

p xx=p yy=p zz=-p　　　　　(5-35)

但对于运动流体,因附加黏性正应力的存在,其正应力一般不等于流体静压力。对于附加黏性正应力Δp xx>0、Δp xx<0、Δp xx=0三种情况,相应有|Δσxx|<p、|Δσxx|>p、|Δσxx|=p。但如果将牛顿流体本构方程式(5 -32)中三个正应力相加,因为p x x+p yy+ p zz=0,所以有

这说明,虽然运动流体的三个正应力在数值上一般不等于压力值,但它们的平均值却总是与静压力大小相等。

特别地,对于不可压缩流体的一维流动,设流动沿x方向,则因为u y=0、u z=0,且根据连续性方程又有,于是由本构方程得:p xx=p yy=p zz=-p。这说明不可压缩流体作一维流动时,其流场中任一点的正应力与静止流体的情况一样,都等于流体静压产生的压应力-p。这正是一维流动分析中,在微元体表面上直接标出压力p作为法向表面力的原因。

将式(5-31)和式(5-32)代入式(5-30),就可将式(5-30)中的应力消去。以其第一式为例得

整理得

对于不可压缩流体,代入得到x方向的运动方程为

同理可得到y、z方向的运动方程,与x方向的运动方程一起组成方程组,有

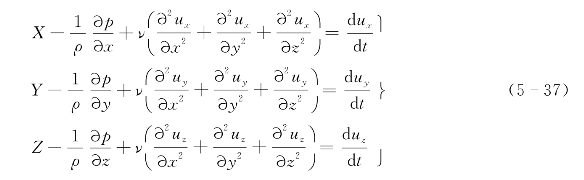
这就是不可压缩黏性流体的运动微分方程,一般称为纳维-斯托克斯方程(Navier-Stokes equation),简称N-S方程,是不可压缩流体最普遍的运动微分方程。以上三式加上不可压缩流体的连续性方程

共四个方程,原则上可以求解方程组中的四个未知量,即流速分量u x,u y,u z和压强p。

由于速度是空间坐标x,y,z和时间t的函数,式(5-37)中的加速度项可以展开为四项,例如

在流速分量u x对时间t求全微分时,指的是某一任取的流体质点的速度对时间的微分,因此就是加速度,此时u x=u x(x,y,z,t)=u x[x(t),y(t),z(t),t]。这种描述方法是拉格朗日法,故函数中的变量x,y和z指的是该质点在运动过程中的位置坐标,因此是时间t的函数,并非独立变量。而式(5 38)右端的四项中的各项又是独立变量x,y,z和t的函数,是欧拉描述方法。这样,式(5-38)就完成了对加速度分量d u x/d t的描述由拉格朗日法到欧拉法的转换。式(5-38)中右边第一项表示空间固定点的流速随时间的变化(对时间的偏导数),称为时变加速度或当地加速度,后三项表示固定质点的流速由于位置的变化而引起的速度变化,称为位变加速度,式(5-38)第二项中表示在同一时刻由于在x方向上位置不同引起的单位长度上速度的变化,u x表示流体质点在单位时间内在x方向上位置变化,因此两者乘积,

表示流体质点的流速分量u x在单位时间内单纯由于在x方向上的位移所产生的速度变化。

这样,纳维-斯托克斯方程又可写成

纳维斯托克斯方程是流体力学中最有用的一组方程之一,它们可以用于建模天气、洋流、管道中的水流、星系中恒星的运动、翼型周围的气流,也可以用于飞行器和车辆的设计、血液循环的研究、电站的设计、污染效应的分析等。