变量描述性统计分析要做哪些变量

7.4.1　主成分分析法

主成分分析是把各变量之间的复杂关系进行简化分析的方法。

在社会经济研究中，为了全面系统地分析和研究问题，必须考虑许多经济指标，这些指标从不同的侧面反映研究对象的特征，但是在很多情况下，这些指标在某种程度上存在着信息的重叠，具有一定的相关性。城市竞争力的分析也是如此。从上述关于关于城市竞争力评价的指标体系的讨论中不难看出，城市竞争力的评价都是多指标的。

实际上，科学研究中所涉及的大多课题往往都比较复杂，因为影响客观事物的因素多种多样，需要考察的变量往往很多。比如说，糖尿病、动脉硬化等疾病，其病因是多种多样的，收集的资料所包含的信息也十分繁杂。然而，重叠的、低质量的信息越多，越不利于医生作出诊断。在大部分实际问题中，很多变量(因素)之间都具有一定的相关性的，人们自然希望能找到较少的几个彼此不相关的综合指标尽可能多地反映原来众多变量的信息。1933年，Hotelling提出的主成分分析(Principal Component Analysis)方法正是实现这一目的的有效途径之一。

主成分分析试图在保证数据信息丢失最少的原则下，对这种多变量的综合数据进行最佳的简化，也就是说，对高维变量空间进行降维处理。很显然，任何识别系统在一个低维空间的运行要比在一个高维空间容易得多。在力求数据信息丢失最少的原则下，对高维的变量空间降维，即研究指标体系的少数几个线性组合，并且这几个线性组合所构成的综合指标将尽可能多地保留原来指标变异方面的信息。这些综合指标就称为主成分。

在这里要讨论的问题是:

(1)基于相关系数矩阵还是基于协方差矩阵做主成分分析。当分析中所选择的经济变量具有不同的量纲，变量水平差异很大，应该选择基于相关系数矩阵的主成分分析。

(2)选择几个主成分。主成分分析的目的是简化变量，一般情况下主成分的个数应该小于原始变量的个数。关于保留几个主成分，应该权衡主成分个数和保留的信息。

(3)如何解释主成分所包含的经济意义。

假设我们所讨论的实际问题中，有k个指标，我们把这k个指标看作k个随机变量，记为X₁，X₂，…，X_k。

主成分分析就是要把这k个指标的问题，转变为讨论p个指标的线性组合的问题，而这些新的指标F₁，F₂，…，F_p(p≤k)，按照保留主要信息量的原则充分反映原指标的信息，并且相互独立。

这种由讨论多个指标降为少数几个综合指标的过程在数学上就叫做降维。主成分分析通常的做法是，寻求原指标的线性组合F_i。

F₁=u₁₁X₁+u₂₁X₂+…+u_k1X_kF₂=u₁₂X₁+u₂₂X₂+…+u_k2X_k

………

F_p=u_1kX₁+u_2kX₂+…+u_kpX_k

满足如下的条件:

(1)每个主成分的系数平方和为1。即

u²₁i+u²₂i+…+u²_ki=1

(2)主成分之间相互独立，即无重叠的信息。即

Cov(F_i，F_j)=0，i≠j，i，j=1，2，…，p

(3)主成分的方差依次递减，重要性依次递减，即

Var(F₁)≥Var(F₂)≥…≥Var(F_p)

为了方便，我们在二维空间中讨论主成分的几何意义。设有一个n个观测点的样本，每个观测点有两个观测变量x₁和x₂，在由变量x₁和x₂所确定的二维平面中，n个观测点所散布的情况如椭圆状，如图7－6中的两种情况所示。由图7－6可以看出，这n个观测点无论是沿着x₁轴方向还是x₂轴方向看都具有较大的离散性，其离散的程度可以分别用观测变量x₁的方差和x₂的方差定量地表示。显然，如果只考虑x₁和x₂中的任何一个，那么包含在原始数据中的经济信息将会有较大的损失。

图7－6　两个不同的样本分析

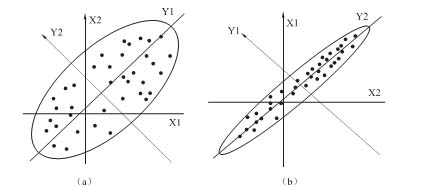
如果我们将x₁轴和x₂轴先平移(注意，轴的平移不改变变量的方差)，再同时按逆时针方向旋转θ角度，得到新坐标轴y₁和y₂。y₁和y₂是两个新变量。

根据旋转变换的公式: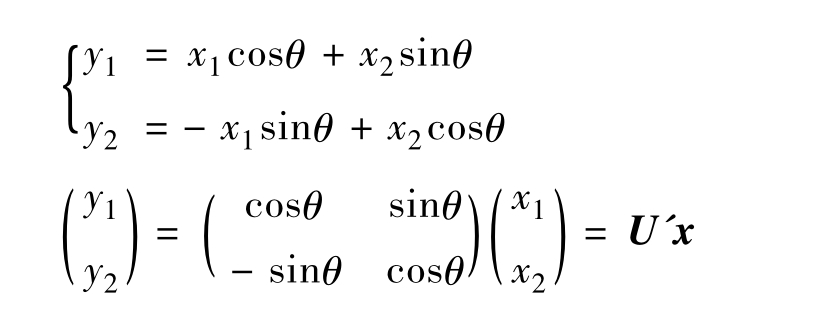

U'为旋转变换矩阵，它是正交矩阵，即有:

U'=U^－1U'U=I

其中，I表示单位矩阵，旋转变换的目的是为了使得n个观测点在y₁轴方向上的离散程度最大，即y₁的方差最大。变量y₁代表了原始数据的绝大部分信息，在研究某经济问题时，即使不考虑变量y₂也无损大局。经过上述旋转变换原始数据的大部分信息集中到y₁轴上，对数据中包含的信息起到了浓缩作用。

y₁和y₂除了可以对包含在x₁和x₂中的信息起着浓缩作用之外，还具有不相关的性质，这使得在研究复杂的问题时避免了信息重叠所带来的虚假性。二维平面上的各点的方差大部分都归结在y₁轴上，而y₂轴上的方差很小。y₁和y₂称为原始变量x₁和x₂的综合变量，变换简化了系统结构使研究抓住了主要矛盾。

为便于讨论，特定义与变量x_i(i=1，2，…，k)相对应的一组观测值(x_i1，x_i2，…，x_in)相对应的标准化变量为: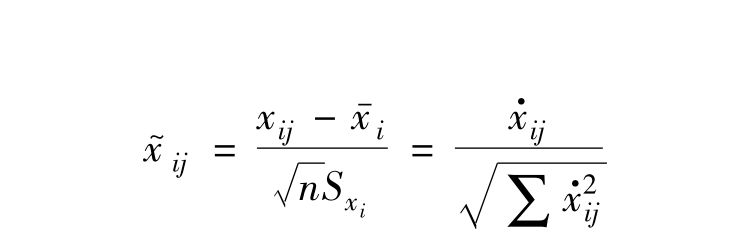

其中: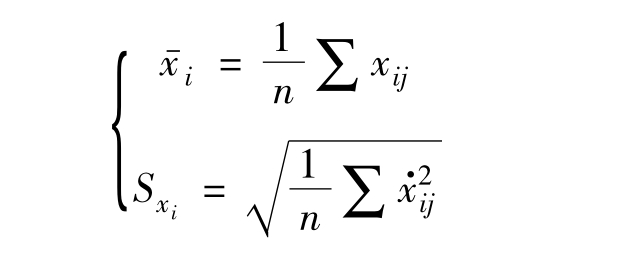

再设有以矩阵形式表示的标准化多元回归模型如: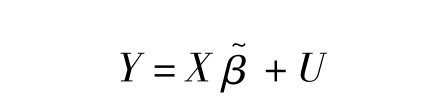(7－1)

其中: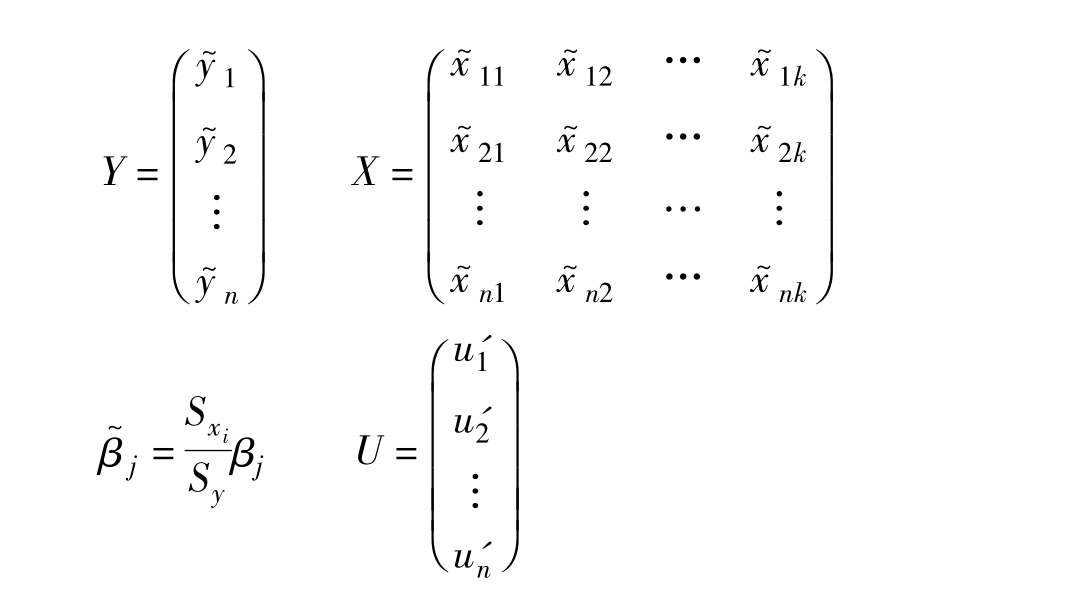

不难看出，标准化变量的样本均值为0。此外，标准化变量的观测值不受坐标原点位置和标度大小的影响，这一点为以相关系数为基础的多重共线性分析带来了很大方便。

由于变量X和Y均已标准化，所以X'X和X'Y都是由相关系数构成的矩阵。即有: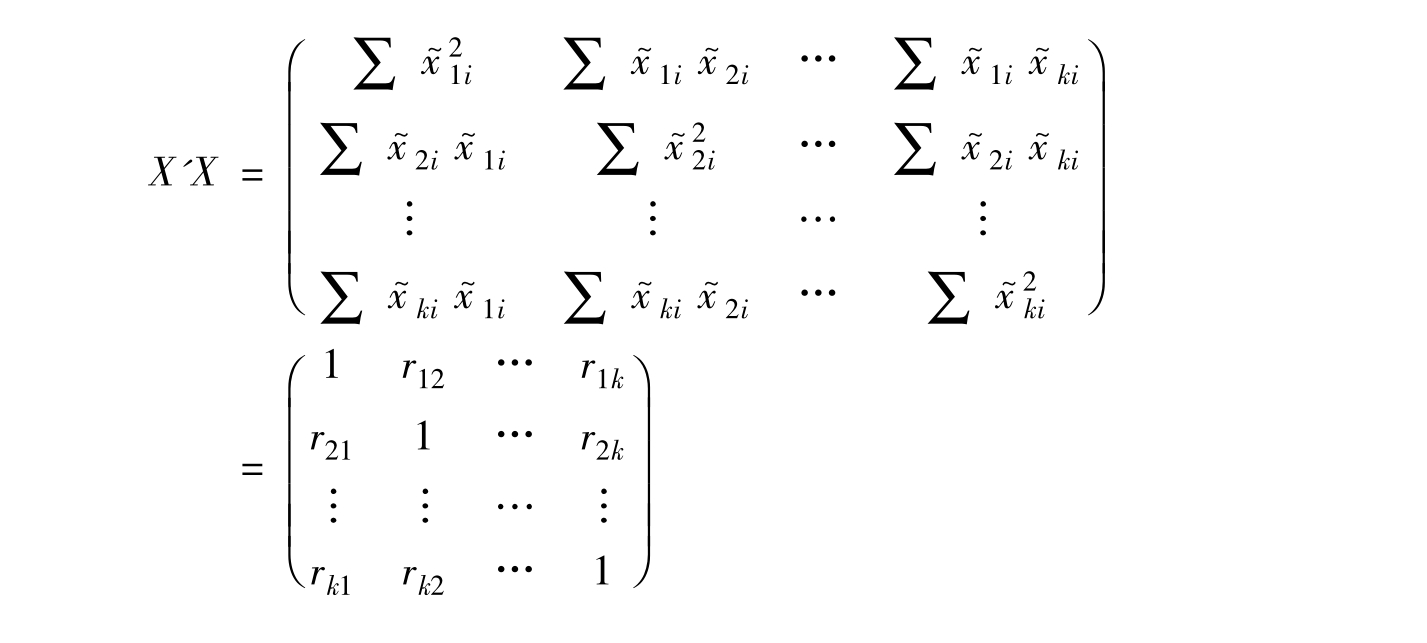

(7－2)

其中: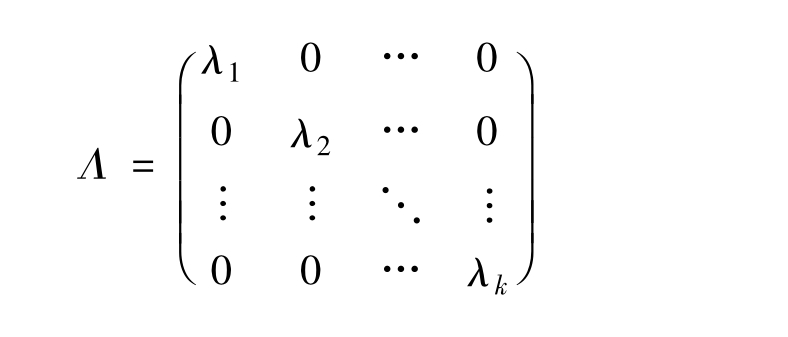

对角元λ₁，λ₂，…，λ_k是X'X的全部特征根且λ₁＞λ₂＞…＞λ_k;正交矩阵C的各列分别为与特征根λ₁，λ₂，…，λ_k相对应的特征向量，即应有:

C=(C₁，C₂，…，C_k)

X'XC_i=λ_iC_i(i=1，2，…，k)

{

根据(6－5)式，现定义:

Z=(z₁，z₂，…，z_k)=XC=(x～1，x^～₂，…，x^～_k)C

显然，应有:

不难看出，新的自变量z_i即为一组正交变量。同时，根据(7－2)式，模型(7－1)可改写为:

Y=X～β+U=(XC)(C'～β)+U(∵C'C=I_k)

或者:Y=Zα+U(7－3)其中:α=C'～β

公式(7－3)就是用正交自变量陈述的模型，亦即用主成分陈述的模型。其中，由于正交矩阵C可逆，且C'(X'X)C=Z'Z，所以k阶方阵Z'Z和X'X为相似矩阵，其特征值相同。这里的变量Z也就是我们所说的主成分。主成分的变量显然具有如下重要性质:

(1)各主成分的均值为0。

(2)各主成分的方差等于计算该主成分时所依据的原始变量的相关矩阵的对应特征根。

(3)各主成分之间互不相关，任意两个主成分的协方差为0。

(4)主成分与原始变量之间的协方差等于特征根与特征向量的乘积。

(5)全部主成分的方差之和等于全部原始变量的方差之和。

(6)贡献率和累积贡献率:第i个主成分的方差在全部方差中所占比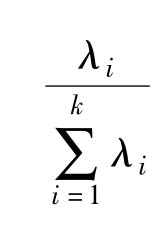

称为

贡献率，反映了原来k个指标包含的信息和综合能力。前p个主成分的总体综合能力

用p个主成分的方差和在全部方差中所占比重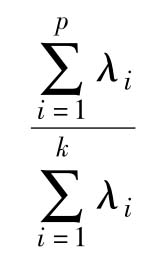来描述，称为累积贡献率。

我们进行主成分分析的目的之一是希望用尽可能少的主成分F₁，F₂，…，F_p(p≤k)代替原来的k个指标。到底应该选择多少个主成分?在实际工作中，主成分个数的多少以能否反映原来变量85%以上的信息量为依据，即当累积贡献率≥85%时，主成分的个数就足够了。主成分个数一般为2到3个。