第二节 多变量描述分析
单变量统计分析忽视了另外因素的影响。对于有多个变量客观存在而又相互影响的资料,采用简单的单变量统计分析是不合理的。多变量统计分析起源于医学和心理学。20世纪30年代它在理论上发展很快,但由于计算复杂,实际应用很少。20世纪70年代以来由于计算机的蓬勃发展和普及,多变量统计分析已渗入到几乎所有的学科。到20世纪80年代后期,由于计算机软件包(如SAS,SPSS,S-PLUS,Stata等)的普遍使用,多变量统计分析变得方便了,因此也更为普及了。多变量统计分析的内容很多,在本章中,只对常用的多变量描述分析:列联表和相关分析作详细介绍,同时对方差分析及回归分析做一些简要介绍。
一、列联表
列联表又称交互分类表,是指同时依据两个变量的值,将所研究的个案分类。列联表的目的是将两个变量分组,然后比较各组的分布状况,以寻找变量间的关系。
这里举一个著名的例子:选用1976—1977年美国佛罗里达州29个地区中,发生凶杀案中被告人判死刑的情况,白人参与凶杀案中被判死刑的比例要比黑人参与凶杀案中被判死刑的比例要高,那是不是在美国社会就不存在凶杀案判罚上的种族问题呢?只要我们稍微仔细地考虑一下,就会发现在凶杀案的判罚上,不仅仅要看被告人的肤色,还要看被害人的肤色。我们把情况分为四种情况:分别为白人杀害黑人,黑人杀害黑人,白人杀害白人,黑人杀害白人,一般来说,后两种情况被告人被判死刑的概率要比前两种情况大得多,这是美国社会的种族歧视在其中所起的作用。在被害人为白人的214起凶杀案中,判死刑的30人,不判死刑的184人;而在被害人为黑人的112起凶杀案中,判死刑的6人,不判死刑的106人。那么被害人的肤色的不同对死刑的判罚有没有影响呢?表9-5是依据变量死刑的判罚与变量被害人的肤色交互分类而成的列联表,用列联表独立性检验可得出被害人的肤色的不同对死刑的判罚有影响,也正是符合了美国社会的实际情况。
表9-5 被害人的肤色与死刑判罚的列联表
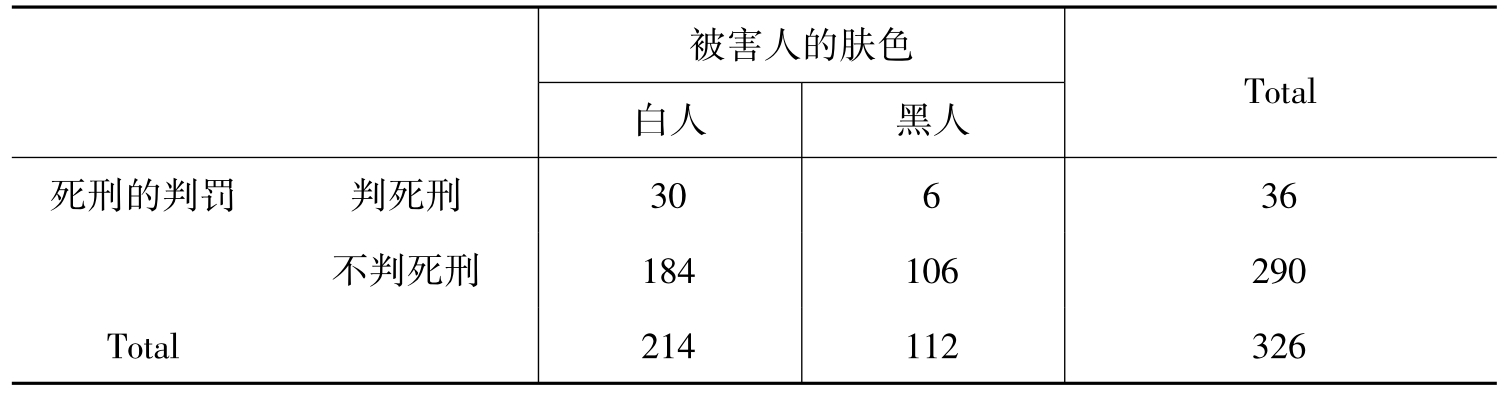
从表9-5中我们可以看出,在被害人的肤色条件下,死刑判罚的情况,因此,这样的表又叫条件次数表。表的最下一行和最右一列分别是被害人肤色和死刑判罚的总次数,称为边缘次数,其分布比例称为边缘分布。其余四方格的次数称为条件次数。每个条件下的分布比例称为条件分布。
条件次数表中的数字是绝对数字,由于各个类别的基数不同,相互间无法进行比较,因而不能看出两变量之间的关系。为了使各个类别可比,我们将表中的绝对数字转换为相对数字——百分数,这样制成的表成为列联百分表。于是,表9-5可以转化为表9-6。
表9-6 被害人的肤色与死刑判罚的列联百分表
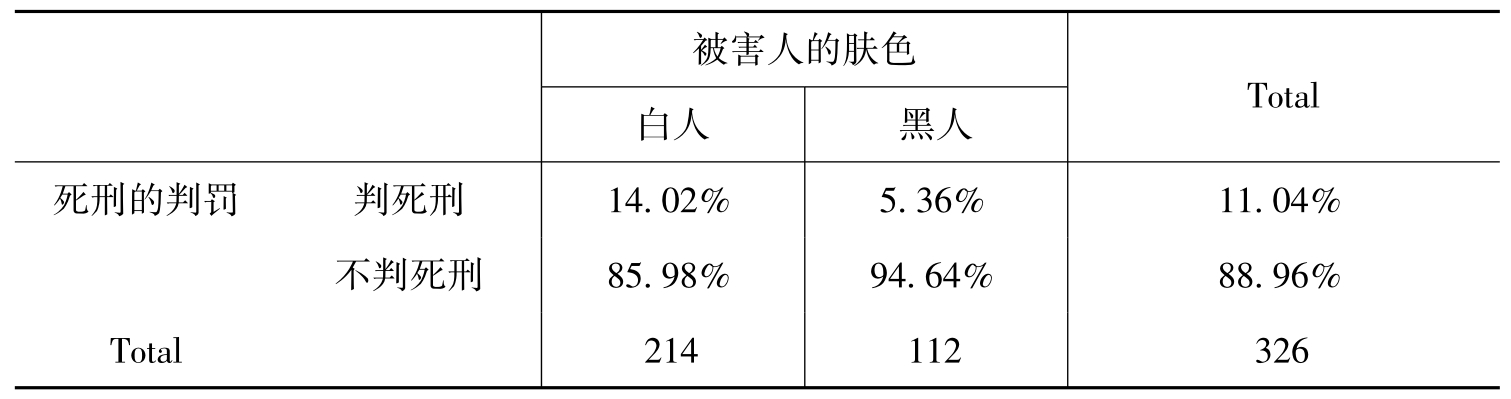
将百分比表中的各列百分比进行比较,就可以得到被害人肤色对死刑判罚的影响,从而可以看出,美国社会实际上存在凶杀案判罚上的种族问题。
在社会科学中,常常采用列联表来记录我们所获得的资料,列联表的资料看起来只是一个一个的资料,但这些由两个或两个以上的类别交叉组合得出的格子,通过运用统计检验方法,能够帮助我们更清晰地分析社会现象。
这里我们引入列联强度这一概念,进一步来衡量列联表中的两个变量紧密程度。
针对2×2表,有两个系数来衡量变量间的紧密程度,其分别为:φ系数和Q系数。
①φ系数(Phi系数)
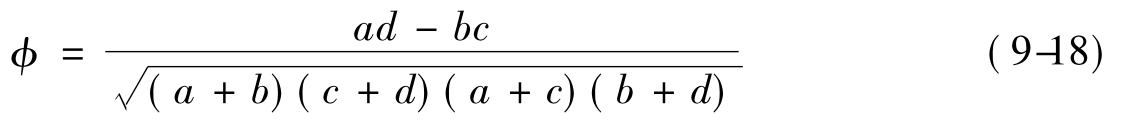
②Q系数

例12 求表9-5的φ系数和Q系数。
已知a=30,b=6,c=184,d=106,代入上述公式可得:
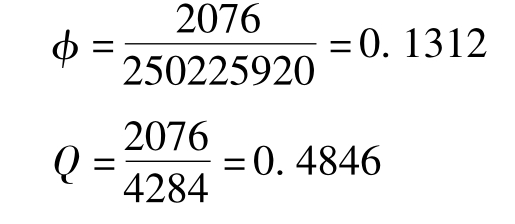
针对r×c表,有三个系数来衡量变量间的紧密程度,其分别为:φ系数、C系数和V系数。
计算此列联强度,需要计算一个重要数值,即χ2值。
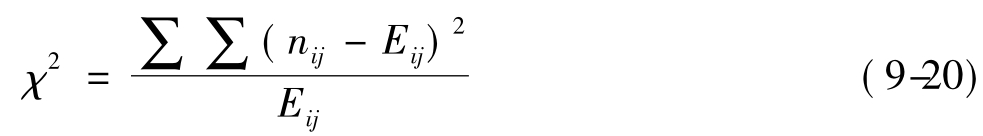
其中nij为实际频数,Eij为理论频数或者期望频数,其计算公式为Eij=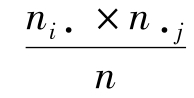 ,其中ni·,n·j为边缘次数。χ2值不仅是计算下列r×c表列联强度的基础,而且也是对变量相关性进行χ2检验的一个统计量。
,其中ni·,n·j为边缘次数。χ2值不仅是计算下列r×c表列联强度的基础,而且也是对变量相关性进行χ2检验的一个统计量。
①φ系数(Phi系数)

这里介绍的φ系数,在2×2表时计算的φ系数是一致的,即当r=2,c=2时,此公式计算的φ系数与2×2表φ系数是一样的。所以2×2表φ系数是r×c表φ系数的特例。
②C系数
针对上面的φ系数无上限的缺点,Karl Pearson在χ2值的基础上创建了C系数,其计算公式(9-22)如下:

③V系数(Cramer's V)
V系数又称Cramer's V系数,克服了C系数永远达不到1的缺陷,其计算公式(9-23)如下:
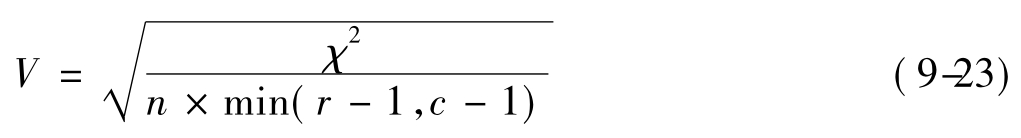
当r=2,c=2时,V系数与φ系数是一致的,而r×c表φ系数与2×3表φ系数是一致的,所以当r=2,c=2时,这三个系数本质上是同一的。
例13 计算表的χ2值,及其三个列联强度系数。
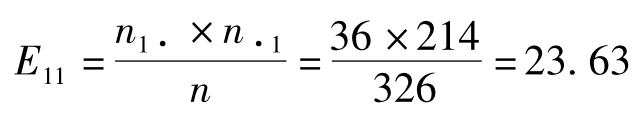 ,同理可得其他的E21=190.37,
,同理可得其他的E21=190.37,
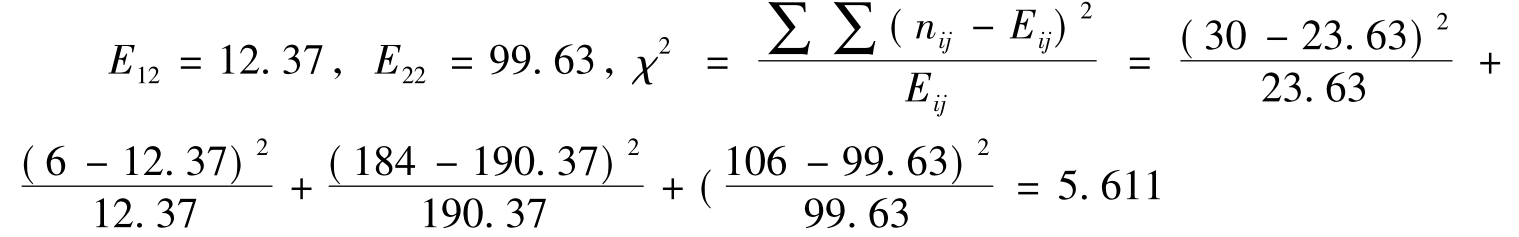
依据得到的χ2值可得三个列联强度系数。
列联表可以通过SPSS软件中的分析(Analyze)菜单下的描述性统计(Descriptive-Statistics)中的交叉表(Crosstabs)子菜单完成,并可以进行列联强度的计算,同时可以进行列联表独立性检验。列联表独立性检验是卡方拟合优度检验(χ2检验)的一个特例,读者可以查阅相关的统计书籍。
二、相关分析
相关分析是对两个变量之间的不确定、不规则的变化关系进行研究,了解两者之间的依存关系和相关程度的方法。根据相关的形式不同,相关关系分为线性相关与非线性相关。如果变量之间的关系近似地表现为一条直线,则称为线性相关;如果变量之间的关系近似地表现为一条曲线,则称为非线性相关或曲线相关。在介绍相关关系之前,我们要先介绍消减误差比例这个概念。
1.消减误差比例
消减误差比例,是指当两个变量具有相关关系时,若用其中一个变量x的数据去预测另一个变量y的数据,应该比不利用x的数据分布,直接用y的分布去预测y能够减少更多的预测误差,即预测结果会更准确一些。简单地说,如果两个变量之间存在相关,那么,就可以根据一个变量去预测或估计另一个变量。估计的准确程度可以作为两个变量之间相关程度的指标。消减误差比例(PRE)的公式:
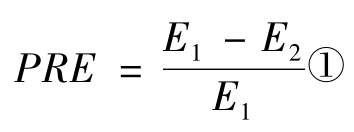 (9-24)
(9-24)
E1:全部误差,即,不知道y与x有关系时,预测或解释y的全部误差;
E2:相关误差,即,知道y与x有关系后,用x去预测或解释y的全部误差;
E1-E2:用x预测或解释y时所减少的误差;
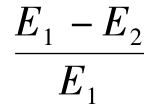 :当用x的变化预测或解释y的变化时能减少多少比例的误差。
:当用x的变化预测或解释y的变化时能减少多少比例的误差。
PER越大,表示x预测或解释y时所减少的误差越多,即x与y的关系越强。PRE的取值区间为[0,1],当E2=0时,PRE=1,说明x与y完全相关,x能百分之百解释y的变化;若E2=E1,则PRE=0,说明x与y之间没有相关关系,x对y无解释力。
定类变量之间或定类与定序变量之间的相关计算公式,直接建立在消减误差比例之上。同时,消减误差比例也是人们解释相关的主要依据。
2.相关系数
用来描述两个变量之间相互变化方向及密切程度的数字特征量称为相关系数。一般用r表示。它的数值范围是-1≤r≤1。根据变量相关方向的不同,相关关系分为正相关与负相关。正相关(r>0)是指两个变量之间的变化方向一致,都是增长或下降趋势,如居民收入增加,居民消费额随之增加,故它们是正相关;负相关(r<0)是指两个变量变化趋势方向相反,如产品单位成本降低,利润随之增加,故它们是负相关。当|r|≥0.8时,视为高度相关;当0.5≤|r|<0.8时,视为中度相关;当0.3≤|r|<0.5时,视为低度相关;当|r|<0.3时,说明两个变量之间相关程度极弱,可视为不相关。注意:此处的r相关强度的概念一般是针对Pearson皮尔逊相关系数而言的,对于同样的数据,不同的计算公式得到的相关系数有可能存在较大的差异,请读者一定要具体问题具体分析。
(1)定类——定类变量、定类——定序变量分析。
用于测量定类——定类变量、定类——定序变量相关关系的系数主要有λ和Tau-y两种。
[6]λ系数
λ相关系数分为对称形式和非对称形式两种。其取值在0~1之间,具有消减误差比例的含义。λ相关系数的对称形式用λ表示,即用于测量的两个变量之间的关系是对等的,即无自变量和因变量之分;其计算公式为:
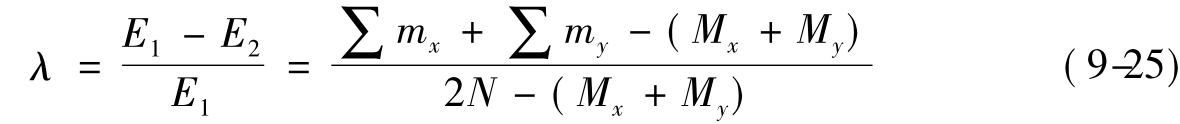
其中:mx表示变量Y的每个取值之下变量X的众数值;my表示变量X的每个取值之下变量Y的众数值;Mx表示变量X的众数值;My表示变量Y的众数值;N表示全部数据或个案的数目。
λ相关系数的非对称形式,用λy表示,即所测量的两个变量间有自变量与因变量之分,x为自变量,y为因变量,其计算公式(9-26)为:

其字符意义与上述公式中字符意义相同。
②τy系数(Tau-y系数)
Tau-y系数简称τy系数,它是测量变量间非对称关系的,其中y为因变量,x为自变量。针对r×c的列联表,其计算公式(9-27)为:
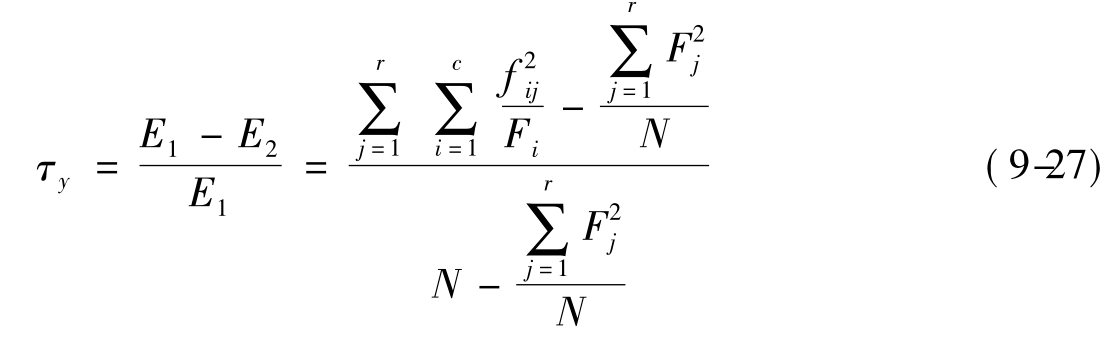
其中:Fj(j=1,2,…,r)表示yj的边缘分布次数;Fi表示xi(i=1,2,…,c)的边缘分布次数;fij表示同属于xi和yi的个案总数,r表示y的变量类别数;c表示x变量类别数;N表示全部数据或个案的数目。
(2)定序——定序变量分析。
用于测量两个定序变量的相关关系的系数有很多,包括G,dy,τa,τb,τc,τs等系数,我们在这里对这些系数作一个简单的介绍。
①G系数(Gamma系数)
G系数,又称Gamma系数,适用于分析两个定序变量间的对等关系,即两个变量无所谓自变量与因变量之分。其取值在-1~1之间,具有消减误差比例的含义。G系数的计算公式(9-28)为:
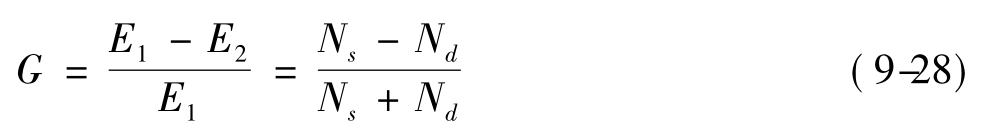
其中:Ns表示同序对数;Nd表示异序对数。同序对数是指两个数据或个案在两个变量上的相对等级相同的对数,不同的便称为异序对数。
②d系数(Somer's d系数)
d系数为Somer所创,所以又称Somer's d系数。分析两个定序变量间的不对等关系,在G系数作了修正,增加了同分对数。当因变量为y时,其计算公式(9-29)如下:

其中:Ns,Nd,Ny与G系数的公式意义相同,
Ny表示仅在y方向的同分对。
③肯氏τa系数(Kendall's tau-a系数)
肯氏τa系数适用于分析两个定序变量间的对等关系,与G系数相类似,只是对分母作了修正,以样本容量N所形成的总对数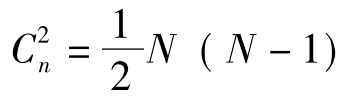 为分母,其计算公式为:
为分母,其计算公式为:

④肯氏τb系数(Kendall's tau-b系数)
肯氏τb系数对τa系数作了修正,增加同分对,分母作如下修正,其计算公式为:
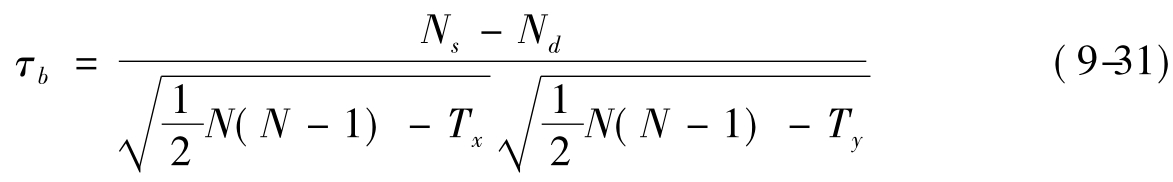
其中:
Ns,Nd,N与τa系数的说明相同,
Tx表示x方向的全部同分对数,
Ty表示y方向的全部同分对数。
⑤肯氏τc系数(Kendall's tau-c系数)
当同分对很多的时候,可以利用此肯氏τc公式,其计算公式(9-32)如下:
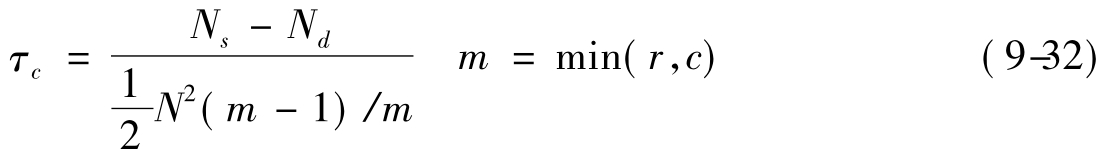
其中:Ns,Nd,N与τa系数的说明相同,
m=min(r,c)(m为r×c等级列联表中r和c值较小者)。
⑥斯皮尔曼(Speaman)等级相关系数rs
斯皮尔曼(Speaman)相关,是Pearson皮尔逊相关的非参数检验的演变,其计算是基于数据的顺序(秩),而非针对数据本身的实际值,对定序变量和数据不满足正态性要求是有效的。其计算公式(9-33)如下:

其中:Di表示第i个调查对象在两个变量上的等级差异,即为第i个调查对象在x变量上的秩与在y变量上的秩的差。
(3)定类——定距变量分析。
在两个变量中,当自变量为定类变量,因变量为定距变量时,采用相关比率来测量二者间的相关程度。相关比率,又称eta平方系数,简写为E2,计算公式(9-34)为:
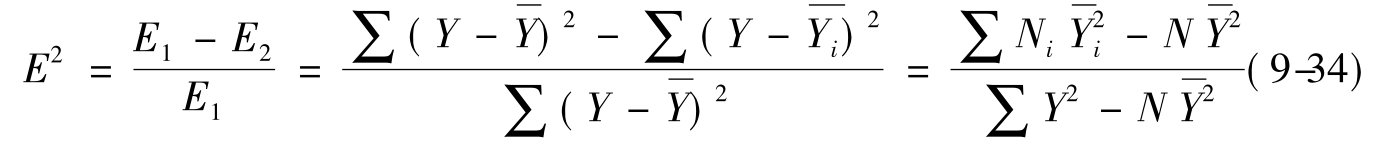
其中: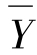 表示因变量Y的平均数,Y i是每个自变量上Xi上因变量的平均数,N为全部样本量数,Ni是每个自变量上Xi上样本量数。
表示因变量Y的平均数,Y i是每个自变量上Xi上因变量的平均数,N为全部样本量数,Ni是每个自变量上Xi上样本量数。
(4)定距——定距变量分析。
相关系数r,又称Pearson皮尔逊相关系数,适用于计算定距变量间的相关分析,是直线相关的最基本方法,一般要求样本N≥50,而且两个变量的分布应近似于正态分布。其计算公式(9-35)为:
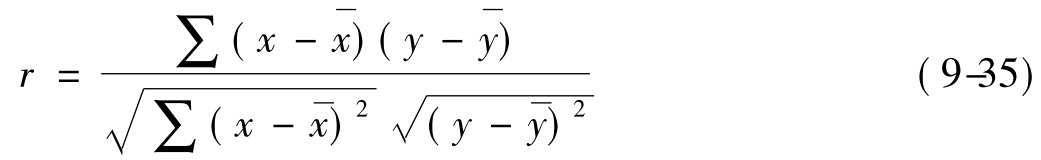
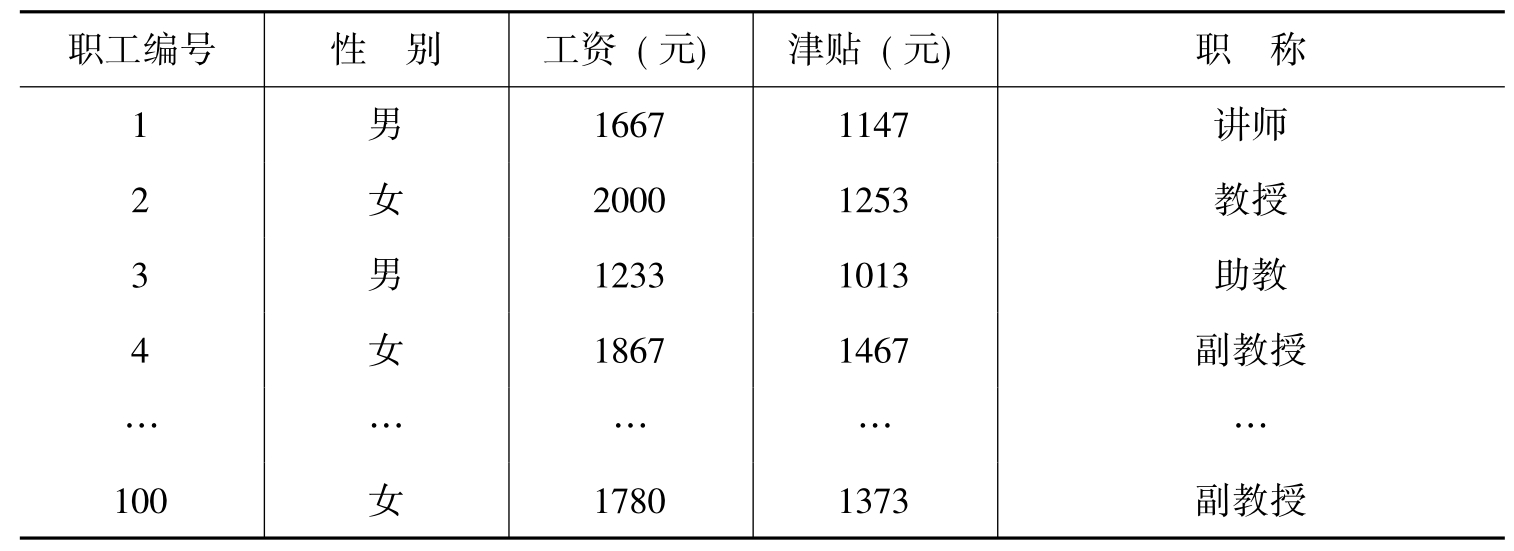
其中: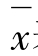 表示变量x的算术平均数,
表示变量x的算术平均数,
y表示变量y的算术平均数。
以上介绍的相关系数大多可以通过SPSS统计工具的分析(Analyze)菜单下的描绘性统计(Descriptive Statistics)中的交叉表(Crosstabs)的子菜单中,以及分析(Analyze)菜单下相关(Correlate)中的双变量相关分析(Bivariate Correlations)子菜单完成。有兴趣的读者可以去查阅以后的章节,以察看具体的SPSS操作方法。
三、方差分析(ANOVA)
方差分析(Analysis of Variance,ANOVA)由英国统计学家R.A.Fisher首先提出,以F命名其统计量,故方差分析又称F检验。其目的是推断两组或多组资料中,它们的均数是否相同,或者检验两个或多个样本均数的差异是否有统计学意义,是关于一个或多个定类变量(因数,称为自变量)和一个或者多个定距变量(称为因变量)的分析。如果处理的是一个定类变量(因数),就叫做单因数方差分析;如果处理的是两个或者以上定类变量(因数),叫做多因数方差分析。如果涉及一个定距变量,叫一元方差分析(ANOVA);如果涉及多个定距变量,叫做多元方差分析(MANOVA)。
表9-7 某高校随机抽取100名职工记录表
一个因数按类别来分,可有多个水平。根据表9-7,如果将性别作为一个因数,那么这个因数有两个水平,分别为男和女,如果将职称作为一个因数,那么这个因数就有多个水平,分别为教授、副教授、讲师、助教,等等。以职称(定类变量)为自变量,以工资(定距变量)为因变量,作方差分析为例,就是推断在职称这个因数下的各个水平(教授、副教授、讲师、助教等)的平均工资是否相同的一种分析方法,即推断各个组(教授、副教授、讲师、助教等)的平均工资是否相同的分析。依据上述说明,不难理解,其方差分析是分析和检验各个水平下的均值是否相同,而不是方差是否相同。但这种分析方法和手段则是通过方差来实现的,所以称为方差分析。
无论是进行ANOVA,还是MANOVA,严格地说,都要求资料满足样本独立,正态性和方差齐性,如果不满足此条件,则我们需要将变量加工,尽量满足条件。而且方差分析的结果只提供了各组均数间差别的总信息,尚未提供各组间差别的具体信息,即尚未指出哪几个组均数间的差别具有或不具有统计学意义。为了得到进一步的信息,可进行多个样本组间的两两比较。
方差分析是比较复杂的,这里只给出一些简单的说明,希望能起到抛砖引玉的作用,方差分析不是本章的重点内容,如需继续了解,则请看后面的章节,或者参阅有关书籍[8][9],不过有一点可以肯定,如果你深刻透彻地了解方差分析,那么你的数据分析水平将会得到极大的提高。
方差分析可以通过SPSS软件中的分析(Analyze)菜单下的一般线性模型(General Linear Model)中的前两个子菜单完成。其中Univariate是用来作一元方差分析,Multi-variate是用来作多元方差分析的。
四、回归分析
回归分析最早是在19世纪末期由高尔顿(Sir Francis Galton)发展的。高尔顿是生物统计学派的奠基人,他的表哥达尔文的巨著《物种起源》问世以后,触动他用统计方法研究智力遗传进化问题,统计学上的“相关”和“回归”的概念也是高尔顿第一次使用的。他是怎样提出这些概念的呢?1870年,高尔顿在研究人类身长的遗传时,发现下列关系:高个子父母的子女,其身高有低于其父母身高的趋势,而矮个子父母的子女,其身高有高于其父母的趋势,即有“回归”到平均数去的趋势,这就是统计学上最初出现“回归”时的含义,也即今日回归模型的前身。
回归分析是一种运用十分广泛的统计分析方法。回归分析按照涉及的自变量的多少,可分为一元回归分析和多元回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。如果在回归分析中,只包括一个自变量(X)和一个因变量(Y),且二者的关系可用一条直线近似表示,则这种回归分析称为一元线性回归分析。其模型为:
Y=a+bX (9-36)
其中a,b为待估参数,在一元回归分析中,利用最小二乘法可以得到
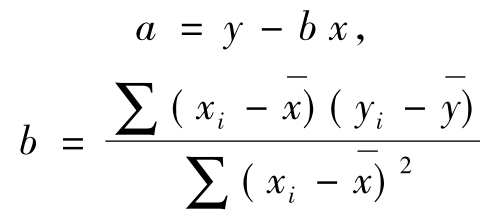
如果回归分析中包括两个或两个以上的自变量(X1,X2,…,Xn),且因变量(Y)和自变量之间是线性关系,则称为多元线性回归分析。其模型为:
Y=B0+B1X1+B2X2+…+BnXn
(9-37)回归分析的主要内容为:
(1)从一组数据出发确定某些变量之间的定量关系式,即建立数学模型并估计其中的未知参数。估计参数的常用方法是最小二乘法。
(2)对这些关系式的可信程度进行检验。
(3)在许多自变量共同影响着一个因变量的关系中,判断哪个(或哪些)自变量的影响是显著的,哪些自变量的影响是不显著的,将影响显著的自变量选入模型中,而剔除影响不显著的变量,通常用逐步回归、向前回归和向后回归等方法。
(4)利用所求的关系式对某一社会过程和现象进行预测或控制。
一般地,对于社会学专业的学生,对其中的数学原理的了解相对较低,关键是对其运算操作过程和结果分析的掌握。回归分析的应用是非常广泛的,统计软件包(SPSS、SAS、EXCEL等)使得各种回归方法计算十分方便。
在SPSS中,我们可以通过SPSS软件中的分析(Analyze)菜单下的回归(Regression)中的子菜单完成。子菜单Linear Regression解决多元线性回归,Curve Estimation解决曲线回归,Nonlinear Regression解决非线性回归,等等。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















