【摘要】：引理5.1［136］ 若X1，X2，…，Xn为独立同分布的随机变量，它们的均值μ，方差为σ2＞0.则对于所有的n，有
首先陈述一个重要的引理.
引理5.1［136］ （Berry-Esseen中心极限定理）若X1，X2，…，Xn为独立同分布的随机变量，它们的均值μ，方差为σ2＞0.则对于所有的n，有
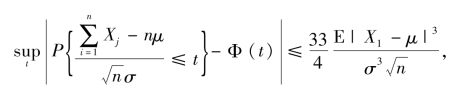
其中Φ（t）为标准正态分布的分布函数，即
下面定理证明了当估计总体的分位寿命ξp时，排序集样本的分位寿命
（p）具有强相合性.
定理5.1 对于任意给定p（0≤p≤1），以概率1有
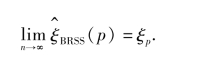
证明：根据生存函数S（t）＝P（T＞t）的单调不增性，对于任意给定的p（0≤p≤1）和正数ε，有
因为
所以
而由经验生存函数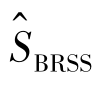
（t）的性质，知对给定的ξp-ε和ξp＋ε，以概率1有
和
故当n→∞时，
再由
（ t）的单调性，得当n→∞时，
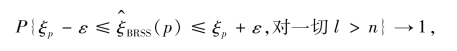
这也就是
定理得证.
下面定理证明了当估计总体的分位寿命ξp时，排序集样本的分位寿命
（p）具有渐近正态性.
定理5.2 如果总体密度函数f（x）在ξp点连续，则当n→∞时，有
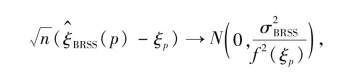
其中
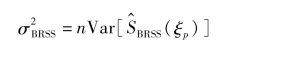
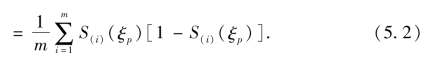
证明：对任给的t，记
其中
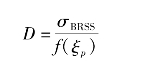
为后面要确定的常数，有
由
（·）的定义知
于是
其中
显然
是独立同分布的随机变量.根据引理3.1，有
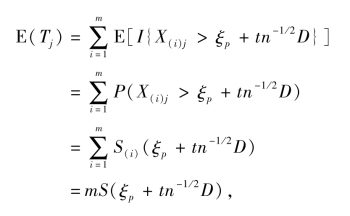
和
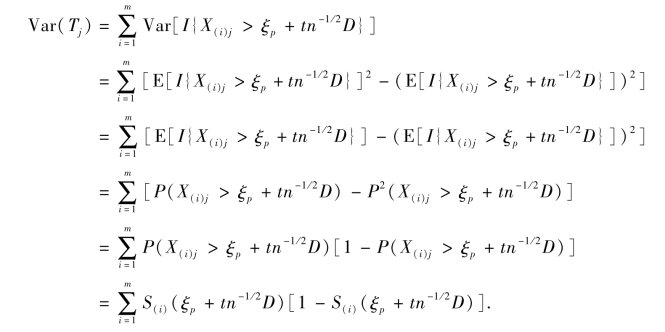
由引理5.1的Berry-Esseen中心极限定理，则对于所有的k，有
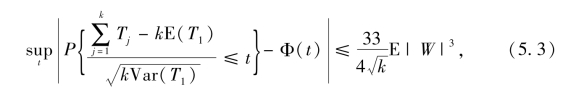
其中
同时，有
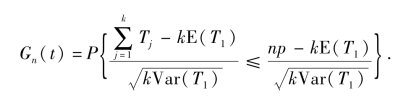
若记
则
由于S（t）在ξp点连续，故n→∞时，有
由不等式（5.3），知
由于f（x）在ξp点连续，于是
显然，当n→∞时，
这样，当n→∞时，
于是
因此，当n→∞时，有
因此，当n→∞时，有
因此，当n→∞时，有
因此，当n→∞时，有
即
于是定理得证.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
