理论假设及推导

11.1.2　理论假设及推导

1.理论假设

（1）投资者全部是风险规避者，即投资者每承担一定的风险，就必然要求与其所承担的风险相应的收益来补偿。如果用纵坐标表示证券或证券组合的预期收益ER，横坐标表示证券或证券组合的风险大小（用标准差衡量，σ），那么该投资者的无差异曲线为向右上方倾斜的二次型曲线。投资组合效用函数具有冯·诺依曼－摩根斯坦（Von－Neumann－Morgenstern，V－NM）效用函数形式，其伯努利效用函数为二次型（其他类型效用函数也常用于投资理论）。

（2）投资者只进行单期投资决策，其投资决策只受当期因素的影响，并且投资者对其证券或证券组合的持有期完全相同，因而该理论实质上是一种静态的投资决策（单期随机现金流模型）。

（3）假设资产的收益和风险状况可以通过资产收益率的均值和方差反映。投资者通过资产收益率的均值和方差来选择投资，同一均值水平上方差小的投资优于方差大的投资，同一方差水平上均值大的投资优于均值小的投资（非饱和性）。

（4）市场不存在不完全信息，所有的市场参与者均能免费获得同样的信息。并且，投资者对市场上各种风险资产的预期收益率和风险大小以及各种资产之间的相关系数都有一致的认识，即齐性预期假设。

（5）不考虑税收、交易成本等因素，即市场环境是无摩擦的；不允许风险资产的卖空交易（在Markowitz最初的研究中他假定风险资产不允许卖空，后来Black引入了卖空假设）。

（6）不考虑无风险资产（所有的资产均为风险资产），投资者不可以按无风险利率进行资金的借贷。后来Tobin修正了这一假设，在模型中引入了无风险借贷假设，见表11.1。

表11.1　Markowitz投资组合模型的拓展

2.理论推导

1）双证券组合收益和风险的衡量

假设投资者投资于两个风险证券，那么该风险证券组合的收益和风险应如何计量呢？假设某投资者将其资金分别投资于风险证券A和B，其投资比重分别为X_A和X_B，X_A＋X_B＝1，则双证券组合的预期收益率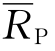等于单个证券预期收益以投资比重为权数的加权平均数，用公式表示：

由于两个证券的风险具有相互抵消的可能性，双证券组合的风险就不能简单的等于单个证券的风险以投资比重为权数的加权平均数。用其收益率的方差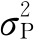表示，其公式应为

式中，σ_AB为证券A和B实际收益率和预期收益率离差之积的期望值，在统计学中称为协方差，协方差可以用来衡量两个证券收益之间的互动性，其计算公式为

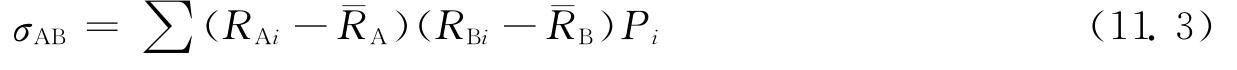
正的协方差表明两个变量朝同一方向变动，负的协方差表明两个变量朝相反方向变动。两种证券收益率的协方差衡量这两种证券一起变动的程度。

表示两证券收益变动之间的互动关系，除了协方差外，还可以用相关系数ρ_AB表示，两者的关系为

相关系数的一个重要特征为其取值范围介于－1与＋1之间，即－1≤ρAB≤＋1。

因此式（11.2）又可以写成：

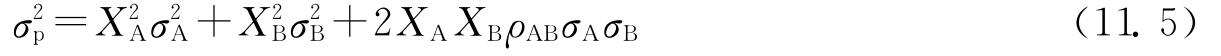
当取值为－1时，表示证券A、B收益变动完全负相关；当取值为＋1时表示证券A、B完全正相关；当取值为0时，表示完全不相关。当0＜ρ_AB＜1时，表示正相关；当－1＜ρ_AB＜0时，表示负相关。

从式（11.2）～式（11.5）可以看出，当ρ＝1时，σ_P＝X_Aσ_A＋X_Bσ_B。而当ρ＜1时，σ_P＜X_Aσ_A＋X_Bσ_B。

根据上面的分析可知，双证券组合的风险不仅取决于每个证券自身的风险（用方差或者标准差表示），还取决于每两个证券之间的互动性（用协方差或相关系数表示）。

为了更好地理解分散化对于降低风险的作用，我们举个例子。假设市场上有A、B两种证券，其预期收益率分别为8%和13%，标准差分别为12%和20%，A、B两种证券的相关系数为0.3。某投资者决定用这两只证券组成投资组合。

根据式（11.1）和式（11.2），组合的预期收益率和方差为

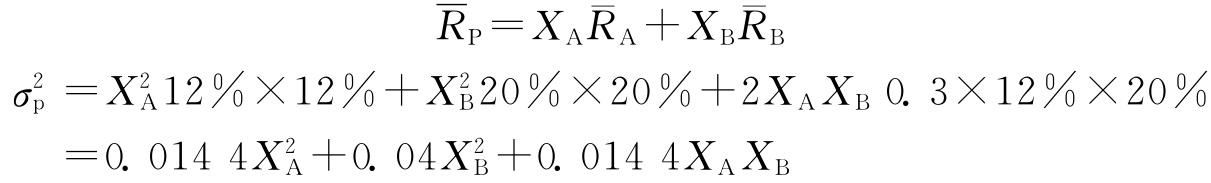
表11.2显示了不同权重下组合的预期收益率和标准差。从表11.2中的第3和第6列可以看出，当证券A的权重从0逐步提高到1（相应地，证券B的权重从1逐步降低到0）时，组合的预期收益率从13%逐步降到8%，而组合的标准差也从20%逐步降低后又回升到12%。其中，当X_A＝0.82，X_B＝1－0.82＝0.18时，组合的标准差最低，为11.45%。

表11.2　不同相关系数下投资组合的预期收益率和标准差

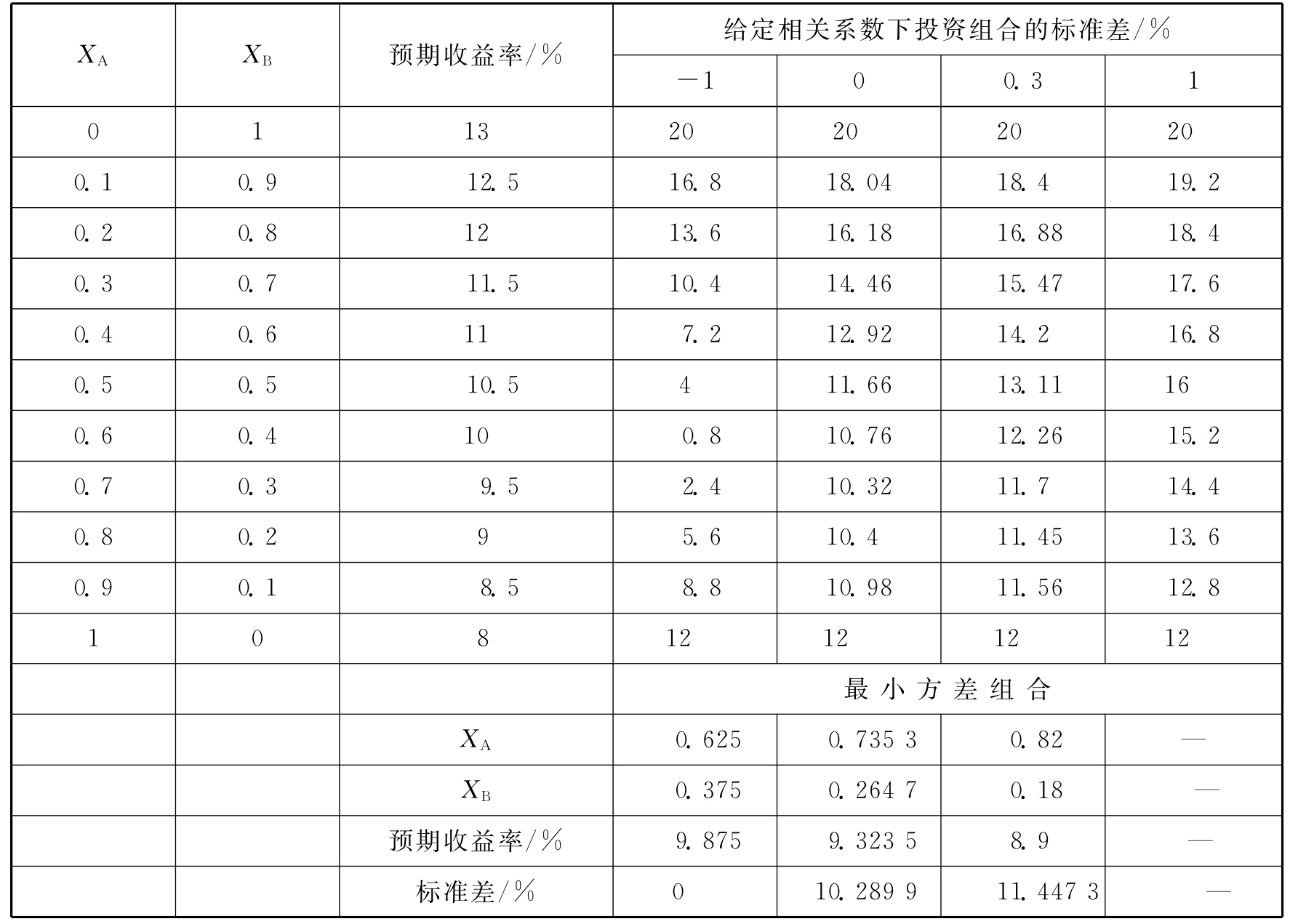
表11.2还给出了不同的相关系数下组合的预期收益率和标准差。从表11.2中可以看出，相关系数对于组合的预期收益率水平是没有影响的。

图11.1给出了不同相关系数下投资权重对预期收益率的影响。图11.2也给出了不同相关系数下投资权重对组合标准差的影响。从图11.2可以看出，除了完全相关外，最低方差组合的标准差均低于A、B两种证券的标准差。这充分说明了多样化的好处。

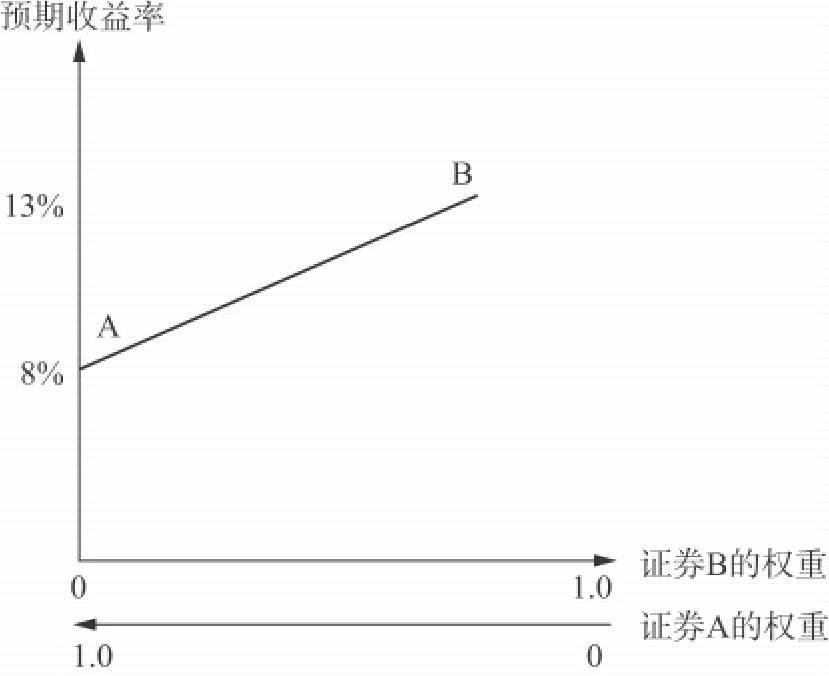
图11.1　投资权重与组合的预期收益率

图11.2　投资权重与组合的标准差

将图11.1和图11.2结合起来看，我们可以得到一个能更直观地反映分散化效果的图形，如图11.3所示。从图11.3中可以看出，当ρ＝1时，双证券A、B组合P的收益和风险关系落在AB直线上（具体在哪一点决定于投资比重X_A和X_B）；当ρ＜1时，代表组合P的收益和风险所有点的集合是一条向后弯的曲线，表明在同等风险水平下收益更大，或者说在同等收益水平下风险更小，ρ越小，往后弯的程度越大；ρ＝－1，是一条后弯的折线。

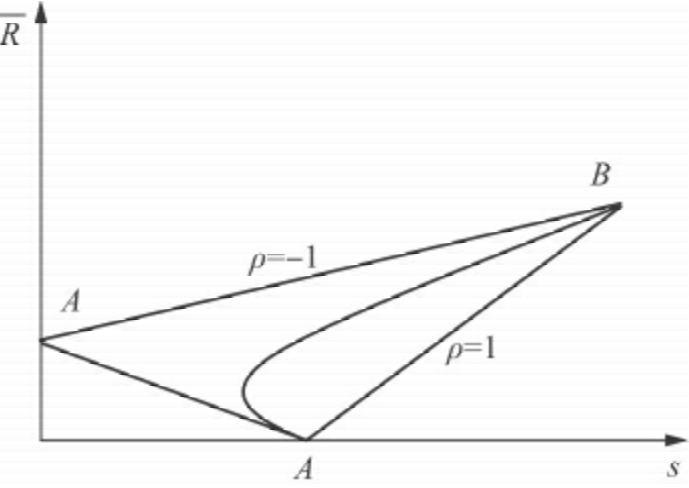
图11.3　双证券组合收益、风险与相关系数的关系

2）三个证券组合的收益和风险的衡量

假设X₁、X₂、X₃分别为投资于证券1、证券2、证券3的投资百分比，X₁＋X₂＋X₃＝1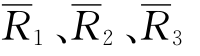为其预期收益率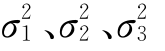，为方差，σ₁₂、σ₁₃、σ₂₃为协方差，则三证券组合的预期收益率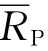为

三风险证券组合的风险为

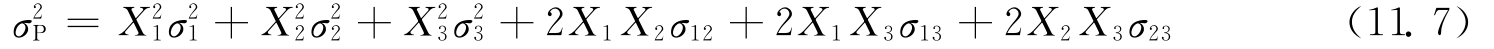
3）N个证券组合收益和风险的衡量

（1）N个证券组合的收益

由上面的分析可知，证券组合的预期收益率就是组成该组合的各种证券的预期收益率的加权平均数，权数是投资于各种证券的资金占总投资额的比例，用公式表示为：

式中，X_i是投资于i证券的资金占总投资额的比例或权数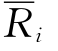；是证券i的预期收益率。

（2）N个证券组合的风险

式中　i——第i项资产的收益率方差；

　　X_i——第i项资产在组合中所占比重；

　　P_ij——资产i与资产j的收益率的相关系数［Cov（R_i，R_j）＝P_ijij；P_ij＝Cov（R_iR_j）/ij］

可行的资产组合集合区域公式（11.9）也可以用矩阵来表示，双加号ΣΣ意味着把方阵（n×n）的所有元素相加，假定n等于4，即该证券组合的方差为以下矩阵中各元素之和，该矩阵称为方差－协方差矩阵（Variance－Covariance Matrix）。

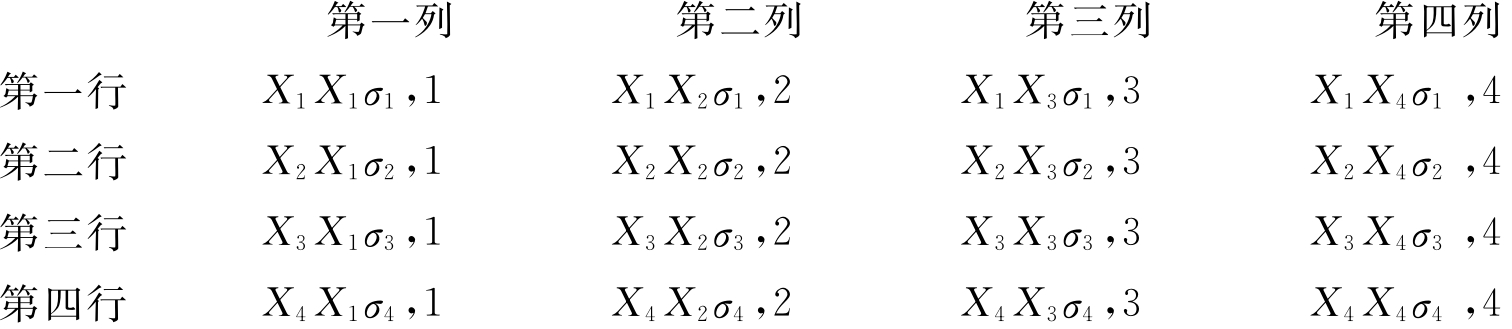
由上可知，证券组合的方差不仅取决于单个证券的方差，而且还取决于各种证券间的协方差。随着组合中证券数目的增加，在决定组合方差时，协方差的作用越来越大，而方差的作用越来越小。这一点可以通过考察方差－协方差矩阵看出来。在一个由两个证券组成的组合中，有两个加权方差和两个加权协方差。但是对一个大的组合而言，总方差主要取决于任意两种证券间的协方差。例如，在一个由30种证券组成的组合中，有30个方差和870个协方差。若一个组合进一步扩大到包括所有的证券，则协方差几乎就成了组合标准差的决定性因素。