基于指数-跳－扩散过程的期权定价模型与模拟分析

一、Ornstein－Uhlenbeck过程

在经典的Black－Scholes模型中，我们假设股票价格服从几何布朗运动，

dSt＝μStdt＋σStdWt

基于这个假设，股票价格服从对数正态分布，常数的期望收益率意味着股票价格会随着时间的推移朝同一方向变化。而事实上，很多时候金融变量价格会呈现出均值回复（mean　reverting）的特征，例如股票、利率等。所谓均值回复是指股票价格无论高于或是低于平均价格都会以一定的概率向价格均值回复，也就是说股票收益率从长期来看是呈负自相关的。俗话说，没有只涨不跌的股票也没有只跌不涨的股票。Fama，French［15］和Lo，Mackinlay［16］率先从对美国纽约股票市场的实证研究中得出股票收益率从长期看呈均值回复的结论。用下列模型可以刻画具有均值回复特征的随机过程。

此模型通常称为奥斯坦－乌伦贝克（Ornstein－Uhlenbeck）过程，模型中可以看到，当St上升到μ以上时，μ－St＜0，这时dSt有可能变为负值，于是St接着会下降朝着μ的方向回复。也就是St的变化尽管有一个趋势，但对这个趋势的偏离不完全随机，St在长期内会回到均值，而回复的时间由参数λ决定，于是资产价格在一定程度上表现出周期性。

O－U过程式（5-26）得不到解析解，但可以通过随机差分方程模拟该过程，对于给定的λ，μ，σ，S0，有以下离散形式：

Si－Si－1＝λ（μ－Si－1）Δt＋σSi－1ΔWi，i∈［1，1000］，Δt＝0．001

对于特殊的O－U过程，可以得到解析解，若St满足：

由于

所以

于是方程的解为：

令b（St，t）＝σeλs，这里的积分是伊藤积分，满足limE n→∞，其中随机变量函数（，）的函数bSi－1i值是取在后点上的，这保证了金融资产价格运动的不可预测性，符合经济意义上的合理信息约束。

还有一类可以得到St的解析解，那就是指数O－U过程。

若St满足随机微分方程

其中α＞0，σ＞0为常数。则称St服从指数O－U过程。

实证研究表明，股票的预期收益率是波动性变化的，而指数O－U过程较O－U过程能更好地刻画股票预期收益率的波动规律。对于资产价格服从指数O－U过程的期权定价公式已有一些文献进行了讨论。本书接下来将在指数O－U过程的基础上考虑跳的因素，也就是在标的资产价格服从指数O－U跳扩散过程模型的假设下，首先得到股票价格的解析解，然后利用Girsanov定理和期权定价的鞅方法获得连续平方看涨期权、看跌期权的定价公式；最后，借助蒙特卡罗数值模拟方法得到期权价值的模拟值。

二、指数O－U跳－扩散过程的模型构造与期权定价方法

考虑在式（5－27）中加入泊松跳。

假设股票价格满足随机微分方程：

其中μ为股票的期望收益率，σ＞0为没有发生跳跃时标的资产收益率的标准差，J＞0是刻画跳跃幅度的随机变量，γ＝E（J－1）＞0，Nt服从参数为λ的泊松过程。

1．λ的求解

令Yt＝lnSt，则根据Ito定理有

令得到

dYt＝（a－αYt）dt＋σdWt＋lnJdNt

进而

由于Y0＝lnS0，两边积分得

从而

故

其中J1，J2，…与J独立同分布。

2．期权定价

假设Y＝F（St，t）为任一衍生证券价格，该衍生证券的标的物股票满足的随机微分方程是式（5－28），由Ito定理有

构造一个资产组合

－1：衍生证券

＋FSt：股票

记该证券组合的价值为

证券组合的价值变化为

式（5－30）中不含有dWt项，而dNt项被解释为无须风险回报，所以该证券组合的瞬时收益率与其他短期无风险证券收益率相同，否则会出现套利机会，即

其中r为无风险利率。

将式（5－29），（5－30）代入式（5－31）整理得

接下来求解方程（5－32）。令St＊＝e－rt　St，则

令若，根据Girsanov定理，由dQ＝ξtdP定义了与P等价的概率测度，令WtQ＝Wt－∫t0βsds，则WtQ是等价鞅测度Q下的标准Wiener过程。

于是St＊为Q－鞅，且解得

进一步地

注意到，至此，结论与讨论股票价格服从支付红利率跳－扩散过程时得到的ST的解式（5－17）很相似，不同之处仅在于式（5－33）中没有红利率q，而在接下来的欧式期权价值的求解原理也一样，于是比对式（5－18），（5－19）得到股票价格服从式（5－28）时的欧式期权价值如下：

欧式看涨期权价值

欧式看跌期权价值

三、基于O－U跳－扩散模型的蒙特卡罗模拟分析

在前面的章节里面讨论了衍生证券的定价问题，得到了衍生证券所满足的随机微分方程及其解。但事实上，更多时候我们得不到方程的精确的解析公式或者解析公式本身比较复杂，例如式（5－34），（5－35），这种情况下可以考虑采用数值计算方法。一般用于对衍生证券的估值有三种数值方法，即蒙特卡罗模拟方法、树图方法和有限差分法。其中蒙特卡罗方法因其数学思想简单而直观得到了广泛应用，本节也将采用蒙特卡罗方法进行数值模拟。

蒙特卡罗方法的主要思想是先建立一个和所求问题有关的概率模型，使得待求的值或者其函数值可以表示成为所建模型的数学期望，然后对模型进行大量地抽样取值，最后用抽样生成的随机变量的算术平均值作为所求解的近似值。即假设待求未知量θ是随机变量η的数学期望，即θ＝E［η］，那么近似确定θ的蒙特卡罗方法是：对随机变量η进行m次重复抽样，产生独立同分布的随机变量序列η1，η2，…，ηm，并计算样本均值¯ηm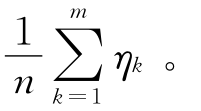＝根据Kolmogorov强大数定律有p（lmi→m∞η¯m＝θ）＝1。因此，当m充分大时，可将η¯m作为待求未知量θ的估计值。蒙特卡罗方法的局限性在于它不能对持有者可以在到期日前提前执行决策的衍生证券进行估值。

进一步，由中心极限定理可得到估计的误差。设随机变量η的方差D［η］＝ση2＜＋∞，对于标准正态分布的上δ／2分位数Zδ／2，有

上述分析可以看到，蒙特卡罗方法的误差是由ση和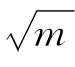决定的。在对随机变量η进行抽样时，若想将精度提高一位数，要么固定ση，将m增大100倍；要么固定m将ση减小10倍。

下面考虑把蒙特卡罗方法具体应用到欧式期权定价问题上来，以欧式看涨期权为例。一个欧式看涨期权的价值等于风险中性测度下对未来期望支付价值的现值，即

其中r为无风险利率，T为到期时间，Q为风险中性测度，K为期权执行价格，f（ST）＝max（ST－K，0）为期权到期时刻价值。

1．对期权价格的数值模拟步骤

步骤Ⅰ：选择一个描述股票价格运动的随机过程式（5－28）。

在以上章节的讨论中知道，为了利用式（5－36）进行计算，需要根据Girsanov定理把f（ST）改写成用WtQ表示的表达式，其中WtQ为Q测度下的标准Wiener过程。在这里，为了表述上的方便，假设一个风险中性世界，于是μ＝r，即股票价格满足：

进一步，假设随机变量J服从对数正态分布，lnJ～N（μJ，σJ2）。μJ为随机变量lnJ所服从正态分布的期望值，σJ为随机变量lnJ所服从正态分布的标准差。

对数正态分布的密度函数为

此时，

γ＝E（J－1）＝exp（μJ＋σJ2／2）－1

步骤Ⅱ：将时间段［0，T］n等分，其中n充分大，每个节点处的时间点为T·i／n。

步骤Ⅲ：式（5－37）离散化为：

其中εi是从标准正态分布中随机抽取的数值，大多数程序语言都编制了抽取0到1之间随机数的程序。一般采用令是0到1之间相互独立的随机数的方法来获取标准正态分布的近似样本值，Ji是从对数正态分布中随机抽取的数值。由于Nt为泊松过程，根据定理1知ΔNi＝Ni＋1－Ni服从参数为λ的泊松分布，即

步骤Ⅳ：给定初值S0以及执行价格K后，随机地独立地每抽取一组εi，Ji，ΔNi的值，根据式（5－38）循环计算就可以模拟出一条可能的价格路径，从而也可以获知在到期时刻的ST值和衍生证券的终值f（ST）＝max（ST－K，0）。

步骤Ⅴ：重复以上步骤，给定初值S0模拟计算出另一条（第l条）可能的价格路径，获得到期时刻SlT值和衍生证券的终值f（SlT），大量的样本路径得出大量的样本终值。比如计算m个终值后，利用算术平均值的计算方法得到E的估计值，最后根据CMC＝e－r（T－t）EQ［f（ST）］最终获得欧式看涨期权的价值。

2．基于不同随机过程的股票价格路径模拟

1）几何布朗运动模型：

dSt＝μStdt＋σStdWt

离散形式为

设定Δt＝0．001，S0＝20，样本路径模拟结果如图5-3，图5-4所示（选取三条）。其中图5-3中设定μ＝0．6，σ＝0．4，图5-4中设定μ＝0．3，σ＝1。

图5-3　几何布朗运动轨迹（μ＝0．6，σ＝0．4）

2）均值回复模型：

dSt＝（μ－αlnSt）Stdt＋σStdWt

离散形式为

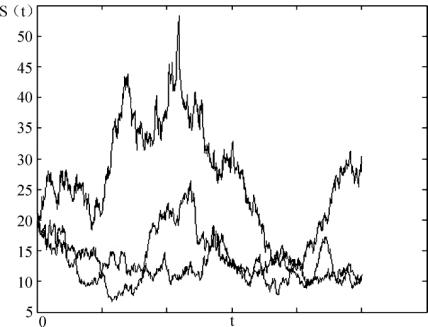
图5-4　几何布朗运动轨迹（μ＝0．3，σ＝1）

设定Δt＝0．001，S0＝20，μ＝0．8，σ＝0．4，样本路径模拟结果如图5－5，图5－6所示（选取三条）。其中图5－5中设定α＝0．2，图5－6中设定α＝0．5。

图5-5　均值回复过程运动轨迹（α＝0．2）

3）含有泊松跳过程的均值回复模型：

dSt＝（μ－λγ－αlnSt）Stdt＋σStdWt＋（J－1）StdNt

离散形式为

设定Δt＝0．001，S0＝20，μ＝0．8，σ＝0．4，α＝0．2，lnJi～N（μJ，σJ2），其中μJ＝0，样本路径模拟结果如图5-5所示（选取一条）。其中图5-7中设定σJ＝0．02，λ＝6，图5-8中设定σJ＝0．1，λ＝1。

从数值模拟的结果可以看到，在几何布朗运动模型假设下，股票呈现出一种较明显的增长趋势。图5-3中参数μ＝0．6，σ＝0．4，图5-4中μ＝0．3，σ＝1。可以看到，图5-3中显示出股票的增长速度较图5-4中股票的增长速度要快，而图5－4中的股票波动性更大，所以μ的值刻画的是股票价格增长的快慢程度，而σ刻画的是股票价格变化过程中的波动程度。

在均值回复模型的假设下，股票不再如图5-3一味地呈现出增长趋势，而是最终在某个值的附近进行震荡，也就是长期来看呈现出一定程度的周期性。在其他参数相同时，考察α值对图形产生的影响。图5-5是当α＝0．2时的走势图，图5－6是当α＝0．5时的图形。显然，α值越大，股票价格回复得越快。

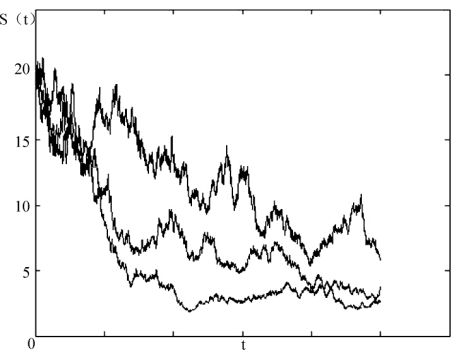
图5-6　均值回复过程运动轨迹（α＝0．5）

图5-7　带跳的均值回复过程运动轨迹（σJ＝0．02，λ＝6）

在含有泊松跳过程的均值回复模型假设下，由于有泊松跳的加入，股票运动呈现出前面两种情况下所未表现出的特征，即股票在正常波动之外有突然上升和下降的点，这便是跳跃的出现。事实上，在计算机上实现的样本路径千奇百怪，这也正是泊松跳过程加入到模型中产生的效果。在这个模型中有两个重要参数σJ和λ，σJ是lnJ的标准差，而（Ji－1）Si是ΔNi的系数，所以某种程度上σJ描绘的是跳跃的幅度大小。由于ΔNi服从参数为λ的泊松分布，泊松分布的数学期望就是λ，从而λ是刻画跳跃出现频率的量。在其他参数相同的情况下，考察σJ和λ的值对图形产生的影响。图5－7是当σJ＝0．02，λ＝6时的路径图；图5－8是当σJ＝0．1，λ＝1时的路径图。可以看到，当λ取值大，σJ取值小时说明跳跃出现得频繁但是幅度小；当λ取值小，σJ取值大时说明跳跃次数少但每次跳跃的幅度较大，所以图5－7比图5－8看起来要更连续。

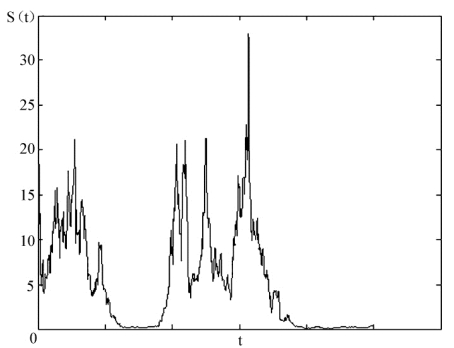
图5－8　带跳的均值回复过程运动轨迹（σJ＝0．1，λ＝1）

3．期权价格数值模拟的程序实现

例如，假设某不支付红利股票的欧式看涨期权，股票价格服从指数O－U跳扩散过程（5－37）。初始股票价格S0＝20，年预期收益率μ＝r＝0．8，波动率σ＝0．4，时间步长Δt＝0．01，其他各项参数为K＝22，T＝1，t∈［0，1］，α＝0．2，lnJi～N（μJ，σJ2），其中μJ＝0，σJ＝0．02，λ＝3。

上述同样的条件，样本路径数量m由50逐渐增加到1000000条，分别得到相应的的期权价值的模拟值和置信区间，结果如表5－1所示：

表5－1　不同样本路径数量m下模拟值与95%置信区间

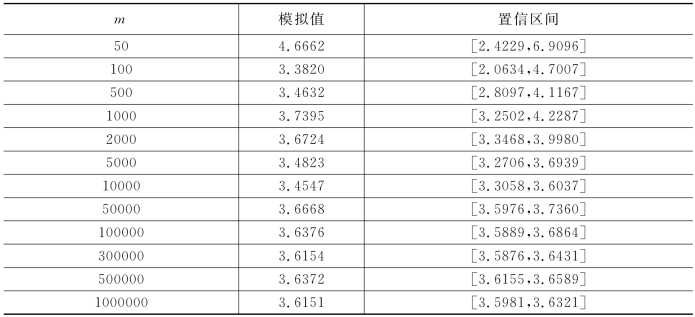
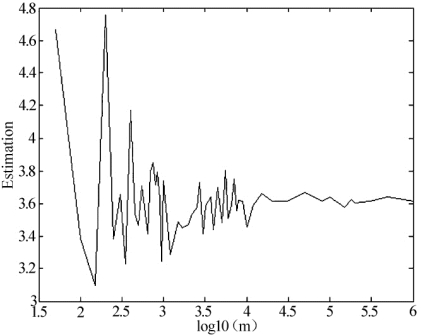
图5-9　蒙特卡罗方法模拟欧式看涨期权价值

图5-9为样本路径m由50逐渐增加到1000000条时所得蒙特卡罗模拟值的曲线图，可以看到随着样本路径的增大，模拟值的波动性逐渐减小，最终稳定在3．6附近取值。表5－1给出了其中部分样本路径数量下所对应的具体模拟值以及置信区间，图5－10所示置信区间位置图对应于表5－1所给数据，由上述图表所示可以得到该期权价值的蒙特卡罗模拟值约为3．6。

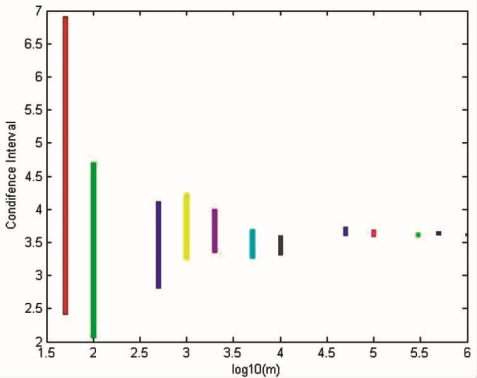
图5-10　置信区间位置图