运筹学模型方法

运筹学是20世纪中叶发展起来的新兴学科和先进的最优化技术，广泛应用于生产经营、工程技术、财政经济、科学研究和社会科学等领域，解决各行各业的生产、计划、设计、分配、管理和决策中的最优问题. 其内容十分丰富，我们只能略举几例，以求举一反三.

例4.20 某工厂生产A、B、C三种产品，需两种原料，各种产品的原料清耗量，每件产品利润及每月可提供的资源限额，见表4-3. 问该厂应如何安排这三种产品的生产，才能使企业获得最大的利润?

表4-3

本题是线性规划问题(LP)，我们用单纯形法来求解，这个方法是美国数学家丹泽格(G·B·Dantzig)于1947年提出的. 线性规划问题，就是一个线性函数在一组线性约束条件下的极值问题，其数学模型的一般形式为: 求一组决策变量x1，x2，…，xn的值，使之满足下列约束条件:

并使目标函数

f=c1x1+c2x2+…+cnxn

取最大值(或最小值). 其中aij、bi、cj均为实常数. 为书写简便，上述模型可表述为

这里maxf、minf分别表示求函数f的最大值和最小值. s. t.意为“在…约束条件之下”.

根据工厂生产情况建立数学模型. 设x1，x2，x3分别表示A、B、C三种产品的产量(件)，则有

满足

增设松弛变量，使约束条件变为等式，由其经济含义，目标函数中松弛变量对应的系数为零，其形式为

Zmax=4x1+x2+5x3+0x4+0x5

现就开始所建的模型作答.

第二步，确定初始基本可行解[1]，填制初始单纯形表，取x1=x2=x3=0，x4=8000，x5=3000，即可满足要求为基本可行解.

确定基本可行解后，将有关数据和符号编入一个表格，编制出初始单纯形表，如表4-4所示. 表4-4的结构共四栏，A栏是对应于第i行基变量的cj值，如第一行的cj就是第一个约束条件，基变量是x4，x5，对应目标函数的c4=0，这里c'1与c4对应，B栏是基本可行解中基变量的名称; C栏是第i个约束条件的右端的值. 在迭代过程中表示同一行中基变量的取值. B栏的基变量可表示为x B=(x4，x5)，其余变量x1，x2，x3为非基变量且x1=x2=x3=0.

表4-4

D栏下面各行元素表为: ①与各变量xj对应的目标函数系数cj; ②决策变量xj;③与xj相对应的A矩阵系数aij，即约束条件方程中xj对应的系数列向量.

表中下面的zj称为机会成本，计算公式为

最后一行为cj-zj称为检验数，即将基变量的函数式代入目标函数式中后非基变量在目标函数中的系数，它表示非基变量转换为基变量后对目标函数的贡献.

第三步，最佳性检验与解判别，表4-4中x1，x2，x3的检验数c1-z1=4，c2-z2=1，c3-z3=5，均为正，且对应的系数列向量满足aij＞0，尚未达到最优，应继续迭代计算.

第四步，确定输入变量和输出变量，输入变量可按下式确定:

max{cj-zj＞0}=ck-zk

xk为输入变量，本例中

max{c1-z1，c2-z2，c3-z3} =max{4，1，5} =c3-z3=5， x3为输入变量，为讨论方便，称输入变量所在的列为输入列，或称K列并以箭头↑K标明.

根据题意考虑x3的生产安排，注意到每生产1个单位需要耗4个单位的甲材和4个单位的乙材. 按甲材供应量x3可生产8000÷4=2000(件)，按乙材供应量x3可生产3000÷4=750 (件). 要满足上述两个要求，x3只能生产750件. 当x3生产750件时，甲材全部耗尽，此时，x5由基变量变为非基变量，x3由非基变量变为基变量，则称x5输出，x3输入. 同理，x5的所在行称为输出行，以箭头L→标明.K列与L行的交点元素a LK为主元素.一般地，在max{cj-zj＞0}=ck-zk下取

L行中的变量为输出变量.

本例θ=min=750 x L=x5.

第五步，进行系数变换，编制新的单纯形表.

由于实际计算比较繁杂，一般采用系数矩阵法，对约束方程组的增广矩矩阵进行初等变换来实现，即在第L行除以a LK使a LK=1，将x K列的其他元素变换为零，这种变换实际上是利用主无消去法进行迭代，由此可得到变换后系数矩阵各元素的变换公式:

根据上述原理进行基变换和系数变换，列出单纯表如表4-5所示.cj-zj行有cj-zj=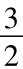＞0，问题还未达到最优，应继续迭代.

第六步，重复第三至第五步操作，由表4-5知，用x1换x3，还可以改善目标函数，方法同前. 表4-6所有检验数cj-zj≤0，表示目标函数不可能再增大，于是得到问题的最优解.

X=(1500，0，0，3500)

表4-5

表4-6

本例给出的目标函数和约束条件都是线性的，其图象是直线或平面(统称为超平面)，从而有最优解可在凸多边形(称为可行域)顶点取到的结论. 在参变量不多的情况下，可用作图或解不等式求解. 在多变量的情况下，我们可以证明如下结论:

(1)若线性规划问题存在可行域，则其可行域

D={X|AX=b，x≥0}

是凸集.

(2)线性规划问题的可行解X=(x1，x2，…，xk，0，…，0)T是基本可行解的充要条件是X的非零分量所对应的系数列向量线性无关.

(3)线性规划问题的基本可行解X对应于可行域D的顶点.

(4)线性规划问题若有可行解，必有基本可行解. 或者说线性规划问题的可行域D为非空凸集，则必有顶点.

(5)线性规划问题若有最优解，则一定可以在可行域D的顶点找到.

单纯形法是寻求解决一般线性规划问题最优解的有效方法，但计算繁复，容易出错，前面介绍的是一种特制的单纯形表格法在实际应用中方便简捷.

线性规划问题很多，在工业、农业、商业、交通运输业、建筑业军事等行业的计划、管理及决策分析得到了广泛深入的应用.构建模型各种各样: 试验建模、统计建模、解析建模、图形建模、概率建模等，方法百花齐放，层出不穷. 但它是数学规划的组成部分. 数学规划可分为静态规划和动态规划. 静态规划又可分为线性规划和非线性规划，这类问题通常与时间无关. 1951年，美国数学家贝尔曼(R.Bellman)等人，根据多阶段决策问题的特点，把多阶段决策问题变换为一系列互相联系的单阶段问题，然后逐个解决，并提出了解决这类问题的“最优性原理”. 在研究了许多实际问题之后，创建了用于寻求多阶段决策问题最优策略的一种新方法——动态规划.

如果一个被考察的对象和外界有物质的、能量的、信息的交换. 外界给予这个对象的称为输入，对象给外界的称为输出. 如果一个过程在时间t0的输出不但与t=t0的输入有关，而且与t≤t0和(或)t≥t0的输入有关，那么这个过程就称为是动态的. 例如，由加速度的定义，一个物体在t时刻的瞬时速度v(t)由以下公式给出.

其中a(τ)是物体在τ时刻获得的加速度，v0是物体在t0时刻的速度. 相对于考察的时间t，v0称为初速度，它是t0时刻以前的力所产生的效果积累. 根据牛顿运动定律，加速度正比于物体所受的外力，即a(t)=F(t)m.其中，m是物体的质量，将它代入式(4.32)，得到

在式(4.33) 中，力F(t) 作为输入，速度v(t) 为输出. 式(4.33)说明v(t) 不但与t时刻受到的力有关，而且与t时刻以前受到的力有关，因此，这是一个动态过程，也是一个动态模型，式(4.32)、式(4.33)称为积分方程. 许多动态过程是用微分方程来描述的，将式(4.33) 两边取导数，得到

这是我们熟知的牛顿第二定律. 式(4.34)是从式(4.33)变化而来，但二者是不同解的. 为了使式(4.33)、式(4.34)同解，对式(4.34)还需加上v(t0) =v0. 这就是所谓初始条件，是t0时刻前的积累.

根据考察的时间，过程可分为两类: 一类称为连续过程，即考察的时间为连续的，充满了一个区间. 上述过程就是连续的，时间t可为区间［t0，t1］中的任意值; 另一类过程称为离散的，如果我们只在时间t的一个序列t0，t1，…，tn，…上考察过程的变化状况.

对于状态变量和决策变量只取连续值: 当状态表示某阶段的出发位置，即每阶段开始所处自然状况或客观条件，通常是一个数或一组数，用变量sk表示，这就是状态变量; 而对某阶段状态的演变方式的选择称为决策，决策也可以用一个数或一组数来表示，就称为决策变量，用xk表示第k阶段的决策变量，从起点到终点的全过程中，每个阶段都有一个决策，这一系列决策所构成的行动方案就称为一个策略. 决策变量的取值往往限于某一范围，如第k阶段的决策集合记为Dk(xk). 过程的演变方式为确定时，这样的动态规划问题，称为连续确定性动态规划问题.

例4.21 某工厂安排一年四季度的生产，已知产品的成本为0.005元×(本季度产量)2，每件存贮费为每季度1元. 每季度的销售量如表4-7所示.

表4-7

假定初始存贮量为0，问应如何安排每季度的生产量和存贮量，在满足销售量的情况下，使总费用为最小?

设xi表示第i季度的生产量，si表示第i季度的存贮量，本例的静态规划模型为

满足

这个问题的动态模型构造如下:

(1)按季度将问题分为四个阶段;

(2)设状态变量sk表示第k阶段初的存贮量; 决策变量为xk，即第k阶段的生产量;

(3)状态转移方程 Sk+1=Sk+xk-qk;

(4)指标函数(第k季度的费用)

(5)指标传递方程

k=4时，有

由于只考虑四个季度，于是令s5=0，由状态转移方程s5=s4+x4-q4，得0=s4+x4-1200，因此得=1200-s4，

k=3时，有

上式为一非线性函数，为求它的最小值，对x3求一阶导数:

令上式为零，得=800-0.5s3，f3(s3)=7500-7s3-0.0025

类似地可求得

全年最小总费用为f1(s1) =11800，通过状态转移方程，可求出相应的决策为

本例的状态转移是确定的. 而有些多阶段决策过程，状态的转移不能完全确定，而按照某种已知的概率分布取值的，处理这类随机性多阶段决策过程的方法，称为随机性动态规划方法.

例4.3 某工厂因生产需要，在近五个月内必须采购一批原料，而据信息未来五月内价格有波动，其浮动价格和概率测得如表4-8所示:

试求在哪一个月以何种价格购入，使其乘购价格的数学期望值最小，并求出期望值.

表4-8

很明显，问题中的价格是一个随机变量，是按已知的概率分布取值的，该问题的动态模型由下述因素确定.

(1)采购期五个月，分成五个阶段;

(2)状态变量sk表示第k个月的实际价格，s'k={500，600， 700}，每月有采购或不采购两种决策，于是令决策变量xk=1表示第k月采购，xk=0，表示第k月不采购，等待，用yk E表示第k月等待的价格期望值;

yk E=0.3fk+1(500) +0.3fk+1(600) +0.4fk+1(700)

(3)指标递推方程

在第5个月时，若所需的原料尚未购入，则无论市场价格如何，都必须采购，不能再等，则有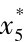=1.

k=4时，

于是第4个月的最优决策为

k=3时，有

所以第3月的最优决策为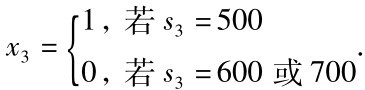

k=2时，有

于是得

k=1，时，有

最后得

依照上述最优策略进行采购时，价格的数学期望为

f1(s1) =0.3×500+(0.3+0.4) +536.26=525.38(元)

我国著名数学家华罗庚先生，在1958年就投身于数学方法在我国工业部门的普及工作，他选择了以改进生产工艺为内容的优选法及处理生产组织与管理问题为内容的统筹法开展普及工作，引进了许多方法，解决了实际工作中许多问题，诸如矿藏储量计算，挂轮问题，各种工业中的原料、染料、元件最佳配比(技术参数)、切削最佳角度、化铁炉最佳电流、如何降低原材料消耗、降低生产成本、机器排序、运输问题、邮递员问题等，取得了丰富的经验与成果.“华罗庚把他的整个生命献给了数学. 他对数学理论的贡献极为广博，极其深厚，极其突出，并有着高度的影响. 他对数学方法应用的普及工作易为普通人民所接受，并具有很显著的效益，他对在中国发展数学事业建立了卓越的功勋.他的数学工作是不朽的，他是当代一位伟大的数学家(段学复:《怀念华罗庚》).”