数学自身的模型方法

以罗巴切夫斯基几何模型为例. 罗氏几何一开始不为人接受，就连罗氏本人也把他创立的几何称之为“虚几何”，是想象的结果. 尽管在逻辑推理上无懈可击，而所产生许多结论与大家通常熟知的事实矛盾. 需要在现实空间中找到一个实际模型来实现罗氏几何.

第一个这样的模型是1868年意大利数学家贝尔特拉米(Bel-trami，1835—1899)给出的. 但只是一个局部的而不是整体的模型;第一个整体的罗氏几何模型是由F·克莱因(1870年)给出的. 他把单位圆作为罗氏平面，而把其中的弦作为罗氏几何中的直线，并适当定义了距离的概念，使得罗氏几何在这一模型中得以实现，从而使人们对罗氏几何有了真实感. 继克莱因之后，法国数学家庞加莱给出了另一个罗氏几何模型.

图4.15

庞加莱在平面上取一个单位圆: {Z∈C: |Z|＜1}，用它来代表整个无限的平面，即非欧空间. S表示单位圆圆周，即S={Z∈C: |Z|=1}，代表无限平面的无限远，并把单位圆内与S垂直的一切圆弧或直线弧作为直线的代表，称之为非欧直线，如图4.15所示，于是单位圆的任一条直径都是非欧直线，而其他的非欧直线都是弯的，进一步定义两点间的距离，设Z1，Z2是单位圆的任意两点，过Z1，Z2作圆弧垂直于ζ，设ζ1与ζ2是该弧在ζ上的两个端点，然后作Z1，ζ1， ζ2，Z2这四点的交比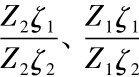，定义

是点Z1到Z2的非欧距离，同时也是这两点所决定的非欧线段的长度.

当Z1=Z2时，Z约定d(z1，Z2) =0.

非欧距离具有与欧氏距离类似的性质，可以验证:

(ⅰ)d(Z1，Z2)≥0(等号仅在Z1=Z2成立);

(ⅱ)d(Z1，Z2) =d(Z2，Z1);

(ⅲ)若Z1，Z2中任一点为Z3，则

d(Z1，Z2)≤d(Z1，Z3) +d(Z3，Z2);

(ⅳ)当Z1(或Z2)沿着非欧直线趋向于ζ1(或ζ2)时d(Z1， Z2)趋向无穷. 这就是，一条非欧直线的非欧长度是无穷，但它用通常的距离概念测量时是有限长的.

而且这种距离在线性变换

之下，是不变的.

因为非欧直线段是普通意义下的圆弧或线弧，非欧直线段的交角就是圆弧的交角; 还可定义非欧圆D和非欧圆周C如(图4.16所示).

这样一个模型适合罗氏的公理系统，除平行公理之外，欧氏几何的全部公理都成立. 而平行公理则变成了: 过直线外一点可以引无穷多条非欧直线与这条直线平行(不相交).

此后，大家都感到信服，于是，我们看到，模型方法在数学内部作用是巨大的.

数学模型方法的着眼点是对外部世界数学秩序的建立，是为解决其他领域而服务的，当然也是为着自身的发展和数学理论的确立.

图4.16