古希腊的数学

现在是时候进入到古典时期了。在这个时期，先是希腊的庞大帝国，然后是罗马人统治了已知世界的大片疆土。他们各自留下相当多的遗产，而他们几乎所有的处世方式都在其消亡后的几百年依然被采纳、被采用。

因为直到最近我们才能够翻译美索不达米亚和古埃及的若干遗迹，去理解这两个文明，所以在很长一段时间内希腊人都被认为与古代世界最伟大的发明和发现息息相关。

苏格拉底（公元前470—前399年）、柏拉图（公元前427—前347年）和亚里士多德（公元前384—前322年）作为数学家的影响将会在本章后面的部分（参见此处）描述，而他们的哲学意义非凡，以至于基督教的神学家在后来都用他们的思维模式来阐述自己的教义，当然里面不会包含他们的异端信仰。所以也难怪这三位古希腊的哲学家在这么长的时间里都在欧洲受到敬仰——他们的思想，再加上《圣经》里头的故事，一直被当作真理，公然对此提出反对并非是明智之举。

然而，尽管他们影响广泛，但我认为他们有一些想法相当奇怪。

最初的哲学家（在希腊语里意思是“爱智慧的人”）一般都是通才，因为那时候，他们并不像我们现在这样拥有人文与科学的专业知识。当中的一些哲学家会利用最纯粹的逻辑去驳斥明显的证据。埃利亚的芝诺（公元前490—前430年）推出一系列悖论去阐明运动是不存在的。他认为，依照逻辑，伟大的战斗英雄阿喀琉斯永远赶不上一只乌龟。因为在比赛开始的时候乌龟已经领先100米了，当阿喀琉斯到达乌龟之前的位置时，乌龟又前进了一点点，阿喀琉斯的追赶是徒劳的。芝诺也提出从弓上放出的箭是静止的，因为每一个瞬间箭都在一个确定的位置。箭在飞行过程中的每一个瞬间都是静止的，所以箭是不动的。这种归约和归谬的方法被报以信任，因为它“证明”了我们不应该相信感知而来的证据，因为那些证据是有缺陷的。因此，逻辑推理被认为是没有缺陷的。这……

由于希腊人对纯逻辑如此热爱，他们很乐于为发展数学去钻研数学。

古希腊人把数学分为两个阵型：理论计算与算术运算。理论计算就是我们今天所说的纯数学——这更多的是研究抽象的东西，而非算算总数那样子——知识分子专门研究这东西，到了今天做这事的人就是研究生了。然而，算术运算就是算数，当时是一种下等的技艺，最好就是留给那些会计算的奴隶去做。

希腊人使用两种计数系统。第一种从公元前500年开始使用，是罗马计数法的前身（参见此处），它与后者的不同之处仅仅是使用了希腊字母，而不是拉丁字母：1就是Ι，5就是Π，10就是Δ，诸如此类。

第二个计数系统在公元前100年替代了第一个计数系统，它仍然基于字母表上的字母。前十个字母，从alpha（α）到iota（ι）代表了数1到10。从这之后的字母开始以10为单位，所以第十一个字母（κ）代表的是20，以此类推，直到（ρ），代表的是100。字母表剩下的字母就是以100为单位的了。所以数字758看起来就是ψ ν η。在这个计数系统中，仍然不可以直接用数本身来运算，所以我们相信进行运算时还是需要借助算子。尽管这些数存在这种局限性，但他们在欧洲也被使用了超过1000年。

希腊人从埃及、美索不达米亚和其他地方的前辈们那里获得了一个知识体系，他们写下并整理了许多数学概念。这些概念直到现在还一直被沿用，我们现在就要对此作一番探究。

希腊最早期的哲学家之一泰勒斯（英文是Thales，读作Thay-leez）诞生于今天土耳其的所在地。他常常被认为是第一个真理科学家。大约在公元前600年的某个时候，泰勒斯开始尝试用自然现象来解析他之所见，而不是通过神迹。

提到数学，泰勒斯与其他古希腊人一样，对几何很感兴趣。他理解相似三角形的原理，并且用这个理论去测金字塔的高度。

本页当中的两个三角形是相似三角形，因为他们的角相等，因此他们的边也互成比例。泰勒斯能够通过测量倒影的长度去判定金字塔的高度。他一直等到自己的影子与自己的高度等长，然后就去测量金字塔影子的长度，以测出金字塔的高度。

大家应该知道毕达哥拉斯，因为普天之下学数学的学生都会学过他的理论。因为他没有留下手写的著作，我们对毕达哥拉斯所知的一切都在他死后很长的时间才被记载。他创立了一个被称为毕达哥拉斯主义的宗教运动，因此关于他的种种，随着时间被不断润饰，毫无疑问也散发出神秘的气息。此外，毕达哥拉斯也被描述成拥有一只金制的大腿，同时也会分身术。

今天，毕达哥拉斯的定理当中最为著名的就是他用来求直角三角形斜边（最长边，直角所对的边）的那一个。口头上，毕达哥拉斯定理是这样描述的：

斜边的平方等于其他两边的平方和。

但这样子就更加精炼：

h2＝a2＋b2

毕达哥拉斯并非探索此定理的第一人。古埃及人也探讨过这个想法，美索不达米亚人也一样——他们的一些作业泥版就刻有与毕达哥拉斯定理相关的问题（参见此处）。从几份不同的原始资料中我们了解到，作为一个年轻人，毕达哥拉斯游历过地中海附近的大片地区，很可能也涉足到更远的地方去学习知识。因此，他似乎有大量机会从别处收集关于这个定理的若干信息。

但为什么这个定理以他的名字来命名？因为毕达哥拉斯是第一个与这个定理有关系的希腊人。而直到最近我们才读得懂象形文字或者楔形文字，所以大家都觉得毕达哥拉斯是独立地把定理钻研出来的。

传说中的毕达哥拉斯

在毕达哥拉斯身上也流传着另一个传说。据说他是第一个弄清弦被拨动时所发音调与其长度关系的人。他还指出当两条弦的长度比是整数时就能够产生和弦。

人们也认为是毕达哥拉斯发现了柏拉图多面体和黄金分割比，这些发现都被柏拉图（参见此处）记录下来。

毕达哥拉斯的狂热信徒是一群有点奇怪的人。这些人热衷于一种苦行的生活，他们避免言谈而且奉行素食。他们是一个非常神秘的团体——揭露团体秘密的人会被判处死刑。毕达哥拉斯主义者也是非常排外的，他们得罪了附近城镇的居民，以至于那里的人烧毁了他们的会面场所，这期间有不少成员被杀。

在毕达哥拉斯主义的中心思想里，数是神圣的。他们相信所有的数都可以写成分数的形式。有一段著名的传说讲的就是一个叫做希帕克斯的倒霉人。希帕克斯是一个毕达哥拉斯主义者，他很肯定自己碰到过一些不能写成分数的数字。在一些天马行空的传说里，毕达哥拉斯叫希帕克斯一起坐船出海，讨论他的异端学说——只有毕达哥拉斯能回来。另一个版本中，希帕克斯被神灵淹死了，以惩罚他对神圣的数所犯下的罪。

无论希帕克斯迎来了什么不愉快的结局，他可能都是第一个发现无理数的人——一些不能写成分数的数，且其小数点后的数字是无限而不循环的。

看看你是否跟得上这段古希腊的反证（参见此处），以看出为什么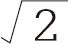是个无理数。

是2的平方根——这个数与自己相乘就得到2。

＝1.4142135623……

如果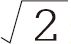能写成分数，那我们就用x/y来表示它的最简形式。

如果x/y是它的最简形式，那么x和y不能同时为偶数。因为如果它们都是偶数，你就可以让x和y同时除以2，这样它们就不是该分数的最简形式。

如果你让分子分母同时平方，你就会得到2＝x2/y2。这意味着x2一定是y2的两倍，因此x2一定是偶数，因为它是某个数的两倍。这反过来又说明了x一定是个偶数，因为奇数×奇数＝奇数。

如果x是偶数，那y一定是奇数。因为，你也可能回想到，x/y是一个最简分数，因此这两个数不能同时为偶数。

如果x是偶数，它一定能被2整除。我们就有x＝2×w。

如果x＝2×w，而x2是y2的两倍，那么就有4w2＝2y2，所以2w2＝y2，也因此y2一定是个偶数，因为它是某个数的两倍。可以推出y就是一个偶数，这跟我们之前的推论y一定是个奇数相矛盾！

如果x是偶数，那么y就一定是偶数。但我们说它一定得是奇数。所以，进而不能写成分数。

苏格拉底（公元前470—前399年）

柏拉图（公元前427—前347年）

亚里士多德（公元前384—前322年）

古希腊最著名的三个哲学家，苏格拉底、柏拉图和亚里士多德经常会被一同提及，因为苏格拉底是柏拉图的老师，而柏拉图又是亚里士多德的老师。他们对西方思想有着巨大的影响。本质上，是他们启发了这些思想。

尽管苏格拉底没有直接对数学做出贡献，他却提出了一种思考问题的方法。这种方法被称为苏格拉底反诘法，为数学难题的求解奠定了逻辑基础。应用苏格拉底反诘法，一个难题可以被分解成一系列更小更易解决的小问题；当这些小问题被逐一击破的时候，求解大难题的方法就应运而生。虽然苏格拉底一般只用这个方法来解决伦理问题，但对于数学和科学难题而言，这个方法也是同样适用的。

柏拉图是苏格拉底的学生，同时也因写了许多本《对话录》而闻名。《对话录》是一本虚构的对话集，说的是苏格拉底与其他很多不同的人对话并提出了许多想法和哲学方面的东西；这读起来有点像一本虚构的课堂记录，记载着一个学生质疑他老师提出的想法。

这些对话集中有一部称为《蒂迈欧篇》，写于公元前360年，柏拉图在当中探讨了几个重要的数学和科学方面的想法。

元素就是《蒂迈欧篇》里提及的第一个主题。现今的原子理论告诉我们，任何已知物质都可以由超过100个元素中的一种或多种组合而成。在他的对话集中，柏拉图第一次提出了四大元素——火，空气，水和泥土——它们各自都有特定的形状。为表敬意，我们把这些元素的形状称为柏拉图立方体。

柏拉图立方体是三维的形状（多面体），其中每一个面都是规则的（每一个角相等，每一条边相等）二维形状（多边形）。例如，一个基于三角形的锥体是由等边三角形构成的，它是一个称为正四面体的柏拉图立方体。

这四种元素，跟我们今天所知的元素很相似，都可以通过结合来构成任何物质。还有另外一个柏拉图立方体——十二面体——它不是一种元素的形状，但它却代表了整个宇宙的形状。

十二面体

在《蒂迈欧篇》里讨论的另一个重要概念是黄金分割比，有时候它被称为黄金比例或者黄金律。

黄金分割点是两个端点之间的最优点，它同时代表了一个数：1.6180339887……——这是其中一个毕达哥拉斯主义者不太喜爱的无理数。与一样，黄金分割比不能写成分数的形式，因为小数位上的数字无限而不循环。这为该数的书写带来不便，所以数学家们使用符号φ（希腊字母phi）来表示它。

另外一个用希腊字母来表示的无理数是3.14159265……：π，从在学校学习圆开始你就会认得这个符号。我们用圆周（圆的周长）除以直径（通过圆心连接圆两端的距离）来得到π。圆有多大是无关重要的，因为你总会得到相同的π值。φ也有相似的几何来源。

如果直线被分成了长短不一的两段，如果（x＋y）的总长度除以x与x÷y的结果相等，那么直线就是按黄金比例来划分的。与π一样，直线的长度是无关重要的——因为你会发现x÷y＝1.618……＝φ。

同样的想法也可以在图形上实现。古希腊人认为长边是短边φ倍的矩形是最有美感的矩形。

人们常说许多重要的雕塑和建筑都用到了黄金分割比。

帕特农神庙是根据黄金分割比来设计的。它的长度与高度、圆柱之间的距离都是根据完美比例来设计。

亚里士多德是马其顿国王的宫廷医生的儿子。这位贵族成了一名影响巨大的哲学家。他受教于柏拉图，随后又成为柏拉图学院的老师。他在许多学科上贡献想法，从政治和伦理到物理和动物学。亚里士多德涉猎广泛，以至于人们觉得他了解任何可知的事物。确实，他的影响贯穿到当今世界的哲学。

对零的选择

亚里士多德以自然直观的方式去对待数。他觉得一个数要有意义当且仅当它能代表某样东西的总数：一堆东西。在亚里士多德的眼中，10个苹果，1个苹果，1/2个苹果和1/10个苹果都是有效的数。然而，如果你连苹果都没有，你就不能把苹果堆起来算总量——零，对亚里士多德而言不是一个数。

亚里士多德主要因他的逻辑学而享誉于世，而那是一系列包含早期逻辑理论的学说。他的理论此后也被划分为不同的分支，有的相当数学化，其他的更加哲学化。

亚里士多德在数学和科学方面的学说着重于通过描述的手段对事物的行为进行解析，而不是利用数字和公式。他是其中一个最先对物体运动（现在我们称这个学科为动力学“kinetics”，希腊语里是“运动”的意思）做出解析的人。亚里士多德在描述中确认时间和空间并非排布在不可分割的区间中，而是连续的，这让他推翻了芝诺的悖论，证实阿喀琉斯是可以追上乌龟的。

尽管我们对古希腊数学家欧几里得了解不多，但我们知道他生活在希腊统治下埃及的亚历山大城，他因写了极具开创性的《几何原本》而闻名于世。欧几里得的《几何原本》无疑是有史以来最重要的数学著作之一，一直到19世纪这本书都被认为是所有学者的基础读物。

虽然欧几里得吸收了他人的想法，但他是第一个利用数理逻辑去证明理论的数学家。这种证明的思想是数学的基础之一。

《几何原本》涵盖大量几何方面的内容，还有一些对数的思考，其中包括质数及其他数列，同时，欧几里得书中的所有几何图形都是通过尺规来构建的。

这一著作被分为十三卷，每一卷的起始部分都是一些定义。有了这些定义，当欧几里得提及点、线、垂直、平面等词语时，读者都能够有个清晰的概念。然后，欧几里得会陈述一系列显然为真的的公理与命题，例如，“所有的直角都是相等的”和“如果A＝B，A＝C，那么B＝C”。

《几何原本》的下一部分称作“命题”，在这里欧几里得会提出一种解决某个数学问题的方法。例如，在卷一的第一个命题里，欧几里得介绍如何画出一个等边三角形（所有的边相等，所有的角都等于），之后他继续去证明为什么那是一个等边三角形。

要是我们大谈质数却不提及博学的数学家埃拉托色尼那就不太对了。埃拉托色尼出生于希腊的一个城邦，地处现今的利比亚。他做过很多开创性的尝试，包括以惊人的精度测出地球的周长，还有引入“地理”一词，这个词在古希腊语中是“描绘地球”的意思。埃拉托色尼的最大贡献是埃拉托色尼筛法。

在查看该筛法之前，让我们先思考一下质数：只有两个因子的数——1和它们本身。因此13是一个质数，因为1和13是仅有的能整除它的数。9不是质数，因为它可以被1、3、9整除，这意味着它有三个因子。1也不是质数，因为它只有一个因子。

基于两个原因，质数是很重要的：

1．任何比1大的整数都能够写成一系列质数相乘的形式。例如，20到30之间的数可以写成下面的形式：

20＝2×2×5

21＝3×7

22＝2×11

23＝23（质数）

24＝2×2×2×3

25＝5×5

26＝2×13

27＝3×3×3

28＝2×2×7

29＝29（质数）

30＝2×3×5

这些形式都是唯一的。所以，对我来说，质数等同于数的DNA。

基本定理

任何比1大的整数都能被唯一表示成一连串质数相乘的积，这叫做算术基本定理。

2．它们十分神秘——质数没有固定的模式，也没有公式可以产生质数。直到今天，数学家们仍然紧锣密鼓地研究质数的本质。

埃拉托色尼筛法应用一个非常简单的原则去寻找一定范围内的质数。2是第一个质数。任何可以被2整除的数都不是质数，因为除了数的本身和1以外，它还拥有2这个因子。

要找出100以内的质数，我们先从2开始。我们排除任何以2为因子的数：4，6，8，等等，一直到100。如果把数记录在网格中，我们可以对被排除的数加阴影，此后的工作都遵从这个模式：

你甚至不需要很熟悉2的乘数表就能做这事——你仅需要每数两个数就在该方格上加阴影。

当你对所有2的倍数都加上阴影后，你转移到另一个未加阴影的数，那就是另外一个质数：3。我们以3为因子，然后排除所有3的倍数，它们当中的一些在第一轮就被排除了。下一个没有加阴影的数是5，这也是一个质数。像之前那样，以它为因子然后排除它的倍数。

你一直做下去，下一个未加阴影的数一定是质数，因为没有比它小的质数能整除它。如果你不停地重复这个过程，最终你会得到一个完整的筛子。翻到58页你就看到它的样子。

无穷多个质数

欧几里得定理证明了有无穷多个质数。我们知道任何一个数都可以通过一系列质数相乘而得到；多亏了我们的筛子，我们也知道100以内的所有质数。我们如何确定有更多的质数呢？让我们用埃拉托色尼筛法去探个究竟。

如果你把已知的所有质数相乘，你会得到一个数。它的下一个数可能是质数，也可能不是。如果这个数是质数，那么我们就得到了一个新的质数。

然而，如果这个数不是质数，那么肯定存在一个我们未知的质数能够整除它——因此在某处还存在另外一个质数。

所以，无论是哪一种情况，我们要么找到了一个新的质数，要么就存在一个未知的比已知质数都要大或者都要小的质数。无论我们的筛子有多大，总会有另外一个质数不在筛子里。因此，质数有无穷多个。

你可以把筛子做得尽可能大去寻找越来越大的质数。这项工作不需要很困难的计算，但却是一个相当乏味的过程——希腊的数学家很可能把它留给一个有学识的奴隶去做。

阿基米德是埃拉托色尼的朋友，他生于地处现今西西里的叙拉古。他是一位著名的科学家和工程师：他发明了阿基米德式螺旋抽水机来抽水灌溉，这工具在今天还被使用。据说阿基米德通过引导太阳光照射到入侵的士兵那里，使他们的战船着火，以保护叙拉古免受罗马战船的攻击。

阿基米德对数学有着显赫的贡献，虽然这些贡献鲜为人知。他计算出π的值，同时强调，当一个多边形增加更多的边数时，它就会越来越接近一个圆。π被定义为圆的周长除以直径的值。要准确测量出圆弧的长度是一件困难的事，但通过测量多边形的边长来算出周长却是容易的。通过把边数较多的多边形近似于圆形，阿基米德用多边形的周长除以其对角线的长度来得到π的值。阿基米德以多达96条边的多边形来进行这种运算。在探究的过程中，他发现π的值在3.143和3.140之间，这与π的实际值相当接近：3.1415……

阿基米德在他的穷举法里无意中用到一个重要思想——相当精确的近似能够逼近到与真实值无异。这个思想被用到数学的其他领域，最显著的也许是约2000年以后牛顿（参见此处）和莱布尼茨（参见此处）的微积分。

阿基米德证明了其他重要的结果，包括圆的面积是π与半径平方的乘积。他也证明了球的体积是其外接圆柱体体积的2/3。阿基米德对他的发现非常满意。有一个球和圆柱的雕塑直立在他的坟墓上。

阿基米德还在伏案研究的时候就死在了罗马士兵的手中。传说阿基米德工作时太投入了，以至于没有对士兵的号令做出反应。士兵感到自己受到侮辱便杀了阿基米德，想必他也得面对狂怒的长官，因为那位长官把阿基米德的智慧视为相当宝贵的科学财富。

随着阿基米德死去，古希腊也走到尽头了，这时候，它的国土被日益强大的罗马帝国吞并。希腊人留下的数学遗产是永恒的，今天的大部分人都见识过本章所提及的许多数学家的一些发现。我认为古希腊最伟大的贡献是使得数学从一种计算的基本需要或者一种为经济服务的工具发展成一门丰富多彩的学科。他们创造的这门学科成为科学的语言，最终让人类从基本原则出发去创立科学学说，使得科学发现是有理论根据的，而不是依赖于一堆为符合观察结果而捏造的式子。没有这样的一种思考模式，艾萨克·牛顿爵士就无法完成他那些开创性的工作。