理想流体的运动方程

连续性方程是流体运动的一个基本方程，这个方程仅反映流体流动时有关运动学方面的关系，没有涉及流体流动中常常遇到的作用力和能量等问题。本节将从牛顿第二定律出发，从作用力和能量的角度，研究流体流动的运动规律，推导和建立理想流体的运动微分方程，并在一定的条件下对运动方程积分，得到理想流体的伯努利积分式和伯努利方程。

5．2．1　理想流体的运动微分方程

如图5-4所示，在理想流体的流场中任取一个由流体质点组成的微小正交六面体微团，该微团各边分别与直角坐标系各轴平行。设各边边长分别为dx、dy、dz，微团形心点M的坐标为(x，y，z)，在t时刻M点上的流速为u，其分量为(ux，uy，uz)，M点上的流体动压强为p，以及密度为ρ。

图5-4　推导理想流体运动微分方程示意图

首先分析该微团在t时刻所受的外力。根据第1章绪论所述，作用在该微团上的外力有质量力和表面力两种。关于作用在该微团上的质量力，可以设表征质量力大小的单位质量力为f，其分量为(fx，fy，fz)。对于作用在该微团上的表面力，由于所考虑的理想流体没有粘滞性而不存在切应力，则表征表面力大小的只有垂直于作用面的流体动压强。又由于所取的微团为微小体，以及流体及其运动要素的连续性，可以用泰勒级数展开的方法得到作用在该六面体微团表面上的表面力。

以Ox轴向为例，质量力在Ox轴向的分力为

作用在abcd和efgh表面上的表面力分别为

根据牛顿第二定律，作用于该微团上的外力在某轴向分力的代数和应等于该微团的流体质量乘以加速度在该轴向的分量，即

或

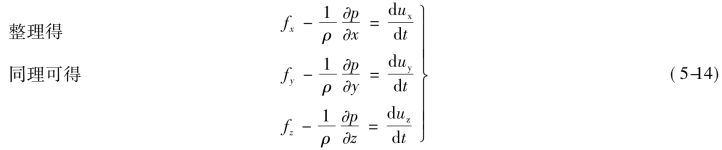
或矢量式

引入式(4-8)表示的流体加速度表达式，上式又可以写成

或矢量式

矢量式(5-15)、式(5-17)中▽=为哈密顿算子。

式(5-14)、式(5-16)称为理想流体的运动微分方程，1755年由欧拉提出，所以又称为欧拉运动方程。当ux=uy=uz=0时，欧拉运动方程则转化为欧拉平衡方程(3-8)。

欧拉运动方程与连续性方程(5-4)联合可以组成封闭的方程组，该方程组含有p、ux、uy、uz四个未知变量，结合具体问题的初始条件和边界条件，可以求解不可压缩理想流体运动的解。由于该方程组为三维非线性偏微分方程组，再加上具体流动问题的初始条件和边界条件通常很复杂，一般不容易求解。但在特定的条件下，可以对欧拉运动方程进行积分，其积分式可以帮助分析流体运动规律，并解决部分流动问题。

5．2．2　理想流体运动微分方程的伯努利积分

对于式(5-16)所示的理想流体运动微分方程，若在下列条件下，可以进行积分求解。

(1)作定常运动，有，即u、p仅为空间坐标的函数;

(2)流体为不可压缩流体，ρ=const;

(3)质量力有势，也就是质量力存在力势函数W(x，y，z)，并且

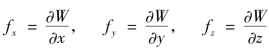
(4)沿流线积分，即由流线方程(4-18)，可得

uxdy=uydx，uydz=uzdy，uzdx=uxdz

根据上述四个条件，理想流体运动微分方程(5-16)可以推导得到

将上式积分，并考虑条件(2)，可得

式(5-18)为理想流体运动微分方程的伯努利积分式。上述积分式表明，在受有势质量力作用下的定常不可压缩理想流体流动中，同一流线上的值保持不变，也就是同一流线上各点的积分常数保持不变。但对不同的流线，式(5-18)中的伯努利积分常数一般是不相同的。

如果某理想流体的流动，所受的质量力仅为重力，以Oz轴向上，则有

fx=fy=0，fz=－g

代入式(3-13)可得dW=－gdz，W=－gz+C

式中，C为积分常数。这时由式(5-18)可得

对于同一流线上的任意两点1与2，上式又可以写成

式(5-18)、式(5-19)即为理想流体伯努利方程。根据流线与元流的定义，流线是元流的极限情况，所以沿流线成立的理想流体伯努利方程对元流同样适用。

5．2．3　理想流体运动微分方程的拉格朗日—柯西积分

对于理想不可压缩流体作无旋流动，并且在有势的质量力作用下，理想流体运动方程式(5-16)可以进行另一类型的积分。

首先将理想流体运动方程(5-16)写成兰姆—葛罗米克运动微分方程

由于是无旋流动，有ωx=ωy=ωz=0，则右边第三项为零。将上述三个方程分别乘以dx、dy、dz，然后相加得

假定质量力为有势力，有式(2-17);并考虑流动无旋，则存在速度势函数φ，且φ满足式(4-48)。则式(5-22)可以写成

对上式积分，有

式(5-24)为不可压缩理想流体运动方程的拉格朗日—柯西积分式。由式(5-23)可见括号内的各项之和与坐标x、y、z无关，则式(5-24)中的积分常数f(t)为时间t的函数。常数f(t)表明流场各点处的积分常数在同一瞬时都相同，而在不同时刻，这些积分常数值则可能会不同。

对于定常流动，f(t)为常数C，并且，则有

若质量力仅为重力，取铅直向上为z方向，即W=－gz，则拉格朗日—柯西积分式变为

定常流时

也称为拉格朗日—柯西积分方程或拉格朗日—柯西方程。

5．2．4　伯努利方程和拉格朗日—柯西方程的意义与区别

伯努利方程式(5-19)、式(5-20)是指在同一条流线上成立，但流动可以是有旋流动;而拉格朗日—柯西方程式(5-27)是指在全流场成立，但流动则为无旋流动。

伯努利方程和拉格朗日—柯西方程中及等项的物理意义和几何意义已在第2章中给出，即在几何意义上这些项分别为位置水头、压强水头及测压管水头;在物理意义上这些项分别为单位重量流体所具有的位能、压强势能及总势能。方程中的第三项与前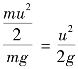两项一样，也具有长度量纲，并且有，即在物理意义上为单位重量流体所具有的动能;在几何意义上为流速水头。伯努利方程中的三项及之和，即位能、压强势能及动能之和，在物理意义上为单位重量流体所具有的总机械能E，即E=z+;在几何意义上为总水头H，即H=z+。

伯努利方程表明理想不可压缩流体在重力作用下作定常流动中，沿同一流线或元流上各点的单位重量流体的位能、压强势能及动能之和保持不变，即总机械能守恒;总机械能中的位能、压强势能及动能三项之间可以相互转化。由此可知，伯努利方程是能量守恒定律在流体力学中的一种特殊表现形式，所以一般也称伯努利方程为能量方程。

拉格朗日—柯西方程则表明理想不可压缩流体在重力作用下作无旋定常流动中，全流场各点的单位重量流体的位能、压强势能及动能之和保持不变。

例5-1如图5-5所示，为一种可利用流体能量转化的原理测量水流流速的简易毕托管。该仪器由两根开口细管组成。已知两管液面高度差为h，试计算被测流体的流速。

图5-5　可测量流速的简易毕托管示意图

解如图5-5所示，A管为一根弯成90°的开口细管，一端垂直向上，另一端放置于被测流体内M点，并正对流体流动方向，这时水流质点流到M点时，受A管管口影响停滞下来，即M点流速为零形成驻点，该点的流速水头全部转化为压强水头，即该管的压强水头中包括了流速水头，使得该管具有较高的液面高度;B管与被测流体相接触一端垂直于流动方向，该管的压强水头不包括流速水头，即该管液面高度较低。

在过M点的同一流线上，取一与M点较近的M0点，并设M0点的流速为u，M0点的压强水头由B管所反映。现对M点和M0点列伯努利方程

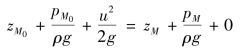
其中由于M点和M0点较近，可以忽略损失。并且zM0=zM，h=，则有