粘性流体运动的微分方程

第七节　流体动力学基础

连续性微分方程是控制流体运动的运动学方程，还需建立控制流体运动的动力学方程，这就是流体的运动微分方程。

一、理想流体运动微分方程

在运动的理想流体中，取微小平行六面体（质点），正交的三个边长dx，dy，dz，分别平行于x，y，z坐标轴。设六面体的中心点o′，速度u→压强p，分析该微小六面体x方向的受力和运动情况。

1.表面力　理想流体内不存在切应力，只有压强。x方向受压面（abcd面和a′b′c′d′面）形心点的压强为：

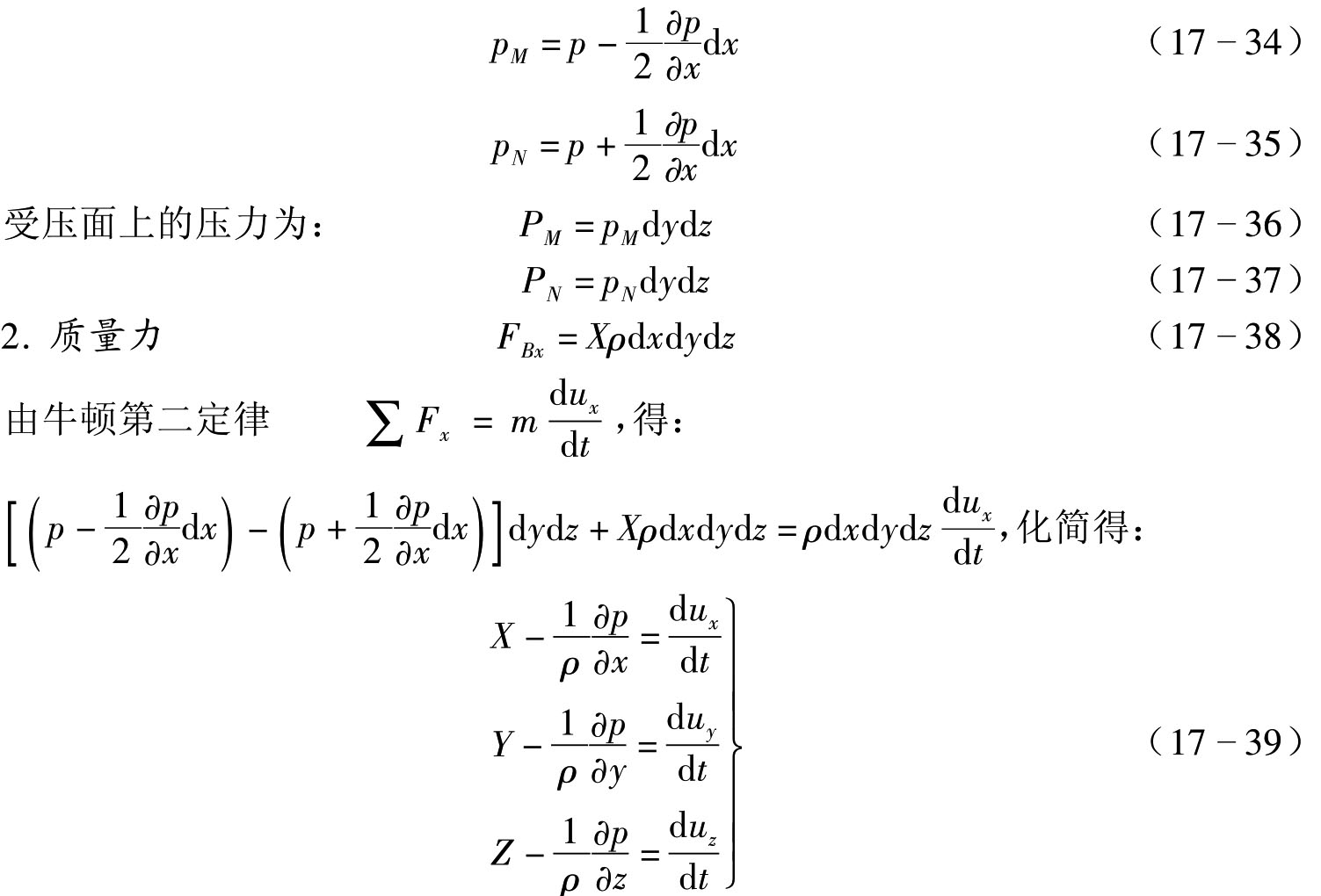
将加速度项展成欧拉法表达式

上式即理想流体运动微分方程式，又称欧拉运动微分方程式。该式是牛顿第二定律的表达式，因此是控制理想流体运动的基本方程式。

1755年欧拉在所著的《流体运动的基本原理》中建立了欧拉运动微分方程式（1740），以及上一节所述的连续性微分方程式。对于理想流体的运动，含有u_x，u_y，u_z和p四个未知量，因此，欧拉运动微分方程和连续性微分方程奠定了理想流体动力学的理论基础。

二、黏性流体运动微分方程

一切实际流体都具有黏性，理想流体运动微分方程存在局限。为此需要建立黏性流体的运动微分方程，本书不做详细推导，仅从物理概念上做简要说明。

（一）黏性流体的动压强

理想流体因无黏滞性，运动时不出现切应力，只有法向应力，即动压强（dynamic pressure）p。用类似分析流体静压强特性的方法，便可证明任一点动压强的大小与作用面的方位无关，是空间坐标和时间变量的函数，即

黏性流体的应力状态和理想流体不同，由于黏性作用，运动时出现切应力，使任一点的法向应力的大小与作用面的方位有关。如以应力符号的第一个下角标表示作用面的方位，第二个角标表示应力的方向，则法向应力p_xx≠p_yy≠p_zz，进一步研究证明，同一点任意三个正交面上的法向应力之和都不变，即

据此，在黏性流体中，把某点三个正交面上的法向应力的平均值定义为该点的动压强以p表示：

如此定义，黏性流体的动压强也是空间坐标和时间变量的函数：

（二）应力和变形速度的关系

黏性流体的应力与变形速度有关，其中法向应力与线变形速度有关，切应力则与角变形速度有关。

流动中某点的动压强p是过该点三个相互正交平面上法向应力的平均值，同某一平面上的法向应力有一定差值，称为附加法向应力，以p′_xx，p′_yy，p′_zz。表示，它是流体微团在法线方向上发生线变形（伸长或缩短）引起的。

切应力与角变形速度的关系，在简单剪切流动中符合牛顿内摩擦定律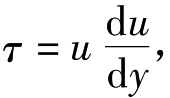，将牛顿内摩擦定律推广到一般空间流动，得出：

（三）黏性流体运动微分方程

采用类似于推导理想流体运动微分方程式（1739）的方法，取微小平行六面体，根据牛顿第二定律建立以应力（包括切应力）表示的运动微分方程式，并以公式（1745）、式（1746）代入整理，使得到黏性流体运动微分方程：

自欧拉提出理想流体运动微分方程以来，法国工程师纳维（Claude.Louis.Marie.Henri.Navier，1785～1836年，法国力学家、工程师）和英国数学家斯托克斯（G. Stokes，1819～1903）等人经过近百年的研究，最终完成现在形式的黏性流体运动微分方程，又称为纳维斯托克斯方程（简写为N-S方程）。N-S方程表示作用在单位质量流体上的质量力、表面力（压力和黏性力）和惯性力相平衡。由N-S方程式和连续性微分方程式组成的基本方程组，原则上可以求解速度场u_x，u_y，u_z和压强场P，可以说黏性流体的运动分析，归结为对N-S方程的研究。

三、流函数

（一）流函数的表达式

对于平面运动，有连续性微分方程，移项得根据曲线积分定理，前式是表达式u_xdy-u_ydx成为某一函数ψ（x，y）的全微分的必要和充分条件：

函数ψ（x，y）称为流函数。由流函数的引出条件可知，凡是不可压缩流体的平面的流动，连续性微分方程成立，不论无漩流动或有漩流动，都存在流函数，而只有无漩流动才有速度势，可见流函数比速度势更具有普遍意义。

流函数具有以下性质：

（1）流函数的等值线是流线

证明：流函数值相等ψ=c，dψ=0，由式得流函数等值线方程u_xdy-u_ydx=0，则：

上式即平面流动的流线方程，流函数的等值线是流线，给流线函数以不同值，便得到流线族。

（2）两条流线的流函数的差值，等于通过该两流线间的单宽流量：

这一性质也可表述为：平面流动中，通过任一曲线的单宽流量，等于该曲线两端流函数的差值。

（3）平面无漩流动的等流函数线（流线）与等势线正交。

证明：对于平面无漩流动，同时存在速度势函数和流函数，由等流函数线方程：

等流函数线与等势线正交，故等势线也就是过流断面线。

（4）平面无漩流动，流函数是调和函数。

证明：因为平面无漩流动：

平面无漩流动的流函数满足拉普拉斯方程，是调和函数。

式中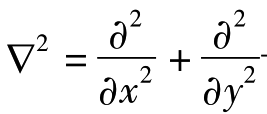：——拉普拉斯算子

式即柯西黎曼条件。φ，ψ满足拉普拉斯方程和柯西黎曼条件，是一对共轭调和函数。

（二）漩流

流体绕固定点逆时针作圆周运动，且速度与圆周半径成反比的流动称为漩流。把坐标原点置于环流中心，则

（三）涡流

流体绕固定点顺时针作圆周运动，且速度与圆周半径成反比的流动称为涡流。把坐标原点置于环流中心，则

等势线方程φ=c，r=c，等势线是以o点引出的射线。

流线方程ψ=c，θ=c，流线是由o点为圆心的同心圆。

以直角坐标系表示：

（郝志永）

参考文献

1　刘鹤年.流体力学.第2版.北京：中国建筑工业出版社，2004

2　丁昀.流体力学教案.兰州交通大学环境学院，2006

3　Fluid Mechanics，Pijush K.Kundu，et al.Cohen and David R Dowling，Academic Press（2011）