单颗粒在气流中的运动方程

第4章　颗粒在气流中的受力与运动

力是改变物体运动状态的根本原因，因此在进行气固两相流动的研究和建立数学模型的过程中，弄清悬浮颗粒在系统中的受力情况至关重要。

在气固悬浮体中颗粒的受力可归结为以下三种类型：

（1）流体对颗粒的作用力——流体力。譬如颗粒周围气流与颗粒间存在相对运动时，流体对颗粒所产生的力，当气流速度大于颗粒运动速度时，气流对颗粒产生曳力；当颗粒运动速度高于气流速度时，颗粒受到运动阻力。

（2）颗粒与颗粒、颗粒与固体壁面间的相互接触、碰撞所产生的作用力——固体力。在气固两相流动中，由于气流中颗粒群在颗粒粒径以及运动速度等方面不完全一致，通常不可避免地存在颗粒与颗粒之间以及颗粒与器壁之间的碰撞与摩擦，形成固体间的作用力。

（3）外界物理场对颗粒的作用力——场力。譬如重力场的存在对颗粒运动所产生的作用力，以及在一些特定情况下，如磁场、电场等对铁磁颗粒或带电颗粒运动所产生的作用力。流体的运动以及它和周围介质的热交换的同时，两者之间还存在着运动与传热的耦合部分。

关于流体的运动和热交换过程在流体力学和传热学的有关著作中都有大量介绍，为了研究悬浮系统的运动与传热我们还必须熟悉颗粒在流体中的受力情况及其运动和颗粒与流体及周围环境的热交换情况。

4.1　颗粒在流体中运动的阻力或曳力

4.1.1　单个颗粒在流体中运动的阻力

当粘性流体绕流物体时，物体总是受到压力和切向应力的作用。在沿物体横截面的流动平面中，这些力的合力F可分解为两个力：与来流方向一致的作用力FD以及垂直于来流方向的升力FL。FD与流体和物体相对速度（uf－up）有关，当物体的运动速度大于流体的流速时，FD即为物体在流体中运动所受到的阻力；当流体流速大于物体运动速度时，FD即为物体所受到流体的曳力。

FD是由流体绕物体流动所引起的切向应力和压力所造成的，故阻力可分为摩擦阻力和压差阻力两种。

摩擦阻力是粘性直接作用的结果，当粘性流体绕物体流动时，流体对物体表面作用有切向应力，由切向应力而产生摩擦阻力。所以，摩擦阻力是指作用在物体表面的切向应力在来流方向上的投影的总和。

压差阻力是粘性间接作用的结果，当粘性流体绕物体流动时，如果附面层发生分离，将在物体下游形成旋涡。图4－1显示的是流体绕流圆柱附面层分离所产生的旋涡，从分离点开始，物体后部所受到的流体压力大致接近于分离点的压力，这样就在物体前后产生压力差，形成压差阻力。压差阻力是指作用在物体表面的压力在来流方向上的投影的总和。压差阻力的大小与物体的形状有很大关系，所以又称为形状阻力，这也是我们通常看到高速运动的物体（如高速列车）尾部设计成尖尾外形的原因，即所谓的流线型，其目的是使附面层的分离点尽量向后推移或不发生分离，减小或避免尾涡区，降低压差阻力。

摩擦阻力与压差阻力之和称为物体阻力。虽然我们从物理上对形成物体阻力的机理已经清楚，但要从理论上来确定一个任意形状物体的阻力，至今还十分困难，通常是通过实验测得。

从工程流体力学的学习中我们知道，单个球形物体在无限扩展的静止粘性流体中运动时，所受到的阻力可用公式（4－1）进行计算

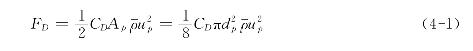
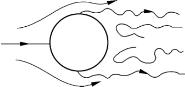
图4－1　流体绕流圆柱附面层分离所产生的旋涡

式中CD为阻力系数，up为球形颗粒在静止流体中的运动速度，Ap和dp分别为为球形颗粒投影面积和直径为流体密度。

阻力系数CD与雷诺数Re有关，即CD是Re的函数。根据牛顿在1710年获得的实验数据以及后人的多次验证表明，雷诺数在700～2×105的范围内，阻力系数差不多为常数。其平均值为CD＝0.44，在此范围内惯性效应为阻力的主要部分，而摩擦效应则可忽略。这时公式（4－1）可简化为

式中ap为球形颗粒的半径。

但是在低雷诺数下，CD随着Re的减少很快增加，图4－2给出了单个圆球以恒定速度在静止等温不可压缩流体内运动时，阻力系数CD随雷诺数Re变化的关系曲线，它是经过大量试验测定精确绘出的。由图可见，对于不同直径的圆球，在不同雷诺数下测得的阻力系数都排列在一条曲线上。当雷诺数Re低于0.3时，阻力系数与雷诺数成反比。相应的阻力公式为

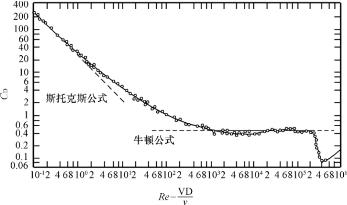
图4－2　单个圆球的阻力系数随雷诺数Re变化的关系曲线

这是Stokes在1850年提出的。这个区域一般可以扩展到Re≤1，通常称为斯托克斯（Stokes）定律区。在斯托克斯定律区内惯性的影响已经很小，可以忽略，摩擦阻力将起主要作用。

在图上还用虚线画出了斯托克斯公式和牛顿公式的相应曲线与实验曲线的比较。由图可见，在Re≤1的范围内，斯托克斯公式可以较好地与实验数据相吻合，而在700≤Re≤2×105的范围内，牛顿公式也近似与实验曲线一致。当Re＞2×105以后，球体的阻力系数突然大幅度地减少，这是由于球体周围流体的流动特性突然改变的原因。这时圆球表面附近的粘性流体层由层流明显地转变为紊流，从而使尾流突然减小，导致阻力系数减少，通常将这个雷诺数值称为高临界雷诺数。高临界雷诺数的具体数值会随球体表面粗糙度的改变而变化，球体表面粗糙时此值减少。

当雷诺数Re在1～700的范围内，若通过分析的方法来说明流体流过圆球周围的流动情况是很困难的，因为在Re＞1时，惯性力将随着雷诺数的增加而逐渐增大。当Re接近于10时，边界层的分离开始发生，在球体后部开始出现涡卷。继续增加Re，旋涡的尺寸与强度逐渐增加。当Re增至100左右时，旋涡区的大小将扩展到与球体体积相当，惯性力也相应不断增长。当Re增至150时，旋涡系统开始出现振荡。当Re为500左右时，旋涡开始脱离圆球形成尾流，这个雷诺数通常就称为低临界雷诺数。当Re为700左右时，惯性力将成为阻力的主要组成部分，流动状态进入牛顿区。上述随着雷诺数的增长，圆球附近流动的变化情况参见图4－3。

图4－3　圆球附近流动的变化情况

为了把斯托克斯阻力公式扩展到较高的雷诺数区，不少学者对此进行了研究。其中最著名的是Oseen所做的工作，他对Stokes的公式作了改进，将远离球面处的惯性力考虑进去并得到了阻力系数的计算公式

这个公式的使用范围可以扩大到Re＜5。如果计算过程是利用计算机进行，还可使用下列计算公式，它的适用范围是Re＜100

对于更大的雷诺数，Rowe建议使用下列公式，其雷诺数适用范围可达Re＜1 000

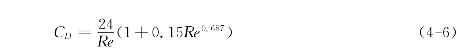
不论是公式（4－4）、（4－5）还是公式（4－6），它们均可写成如下形式

对于不同的Re范围，F＊具有不同的表达形式。

上述各公式也可用于非球形或其他不规则形状的颗粒，这时颗粒直径应按前面所述的投影直径计算。

当流体为很稀薄的气体或颗粒尺寸很小时（小于1μm），颗粒尺寸与流体分子的平均自由碰撞距离（约0.1μm）相比比较小，在颗粒表面上将出现分子滑动并使阻力减少，这时需要对阻力计算公式进行修正。一个比较简单的修正方法是在斯托克斯定律区的阻力系数计算公式中，对雷诺数乘上一系数Cu，该系数称为坎宁安（Cunningham）校正系数

Cu的值为

Cu＝1＋AKn

式中，称为克努森（Knudsen）数，其中Λ为气体的平均分子自由程，对于标准状态下的空气，Λ＝6.53×10－8m。

以上所介绍的所有在静止流体中运动的球体的阻力系数计算公式都可以很方便地应用于流体和颗粒同时运动的多相悬浮系统，唯一需改动的是将所有公式中的up改为颗粒与流体的相对速度（uf－up），这里uf是流体的运动速度，而up为颗粒的运动速度。

在多相流体动力学中，颗粒的运动阻力通常用松弛时间的倒数与颗粒和流体的速度差的乘积表示

4.1.2　颗粒群的运动阻力、沉降速度和松弛时间

在气固悬浮系统中，随着颗粒相浓度的增加，当单个颗粒四周的流体边界层的厚度超过颗粒间间隔的二分之一时，就不能将单个球体颗粒的阻力系数应用于颗粒群了。Kaye 和Boardman发现当颗粒的容积份额大于5%时，颗粒的自由沉降就会受阻，并且自由沉降速度也不再遵循斯托克斯定律。这就是说，即使在低速下，要把Stokes的解推广到较为密集的颗粒群去也是十分困难的。在这种条件下，阻力系数将是雷诺数Re和孔隙度ε的函数

式中CDS为单个颗粒的阻力系数，其中Re应根据单个颗粒在无限流体内自由沉降的终端速度uts计算为颗粒直径分别为流体的密度和动力粘度。

Wen进一步确定了φ（ε）的具体表达式：当Re＞500时，φ（ε）＝ε－4.78；当Re＜0.2时，，作为平均可取。

据此，颗粒群的自由沉降速度可通过下式给出：

对于空隙率ε＜0.8的垂直输送管道，Wen建议采用Ergun的流化床压力降公式来计算流体和颗粒群间的阻力损失。根据厄冈（Ergun）方程，对球形颗粒有

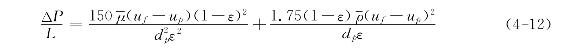
式中除已有符号外，ΔP代表管段压力降，L表示计算管段的长度。

Soo又在这个公式的基础上引用前面介绍的流体与颗粒作动量交换的松弛时间的概念，进一步计算了颗粒在流体中运动的松弛时间和阻力系数。考虑到一定容积内，颗粒群所受到的阻力应该是这个容积内每个颗粒所受的阻力。在不考虑重力影响的情况下，应为颗粒质量mp与松弛时间的倒数F和流体与颗粒间速度差（uf－up）的重量级积，从而获得：

式中mp为每个颗粒的质量，F为流体与颗粒群动量交换松弛时间的倒数；uf为流体在颗粒间隙中流过的速度；up为颗粒速度；NL为长度L上的平均颗粒数；NA为垂直于L方向单位投影面积上的平均颗粒数；lp为颗粒间距；Ap为按每个颗粒均分的截面积。因此Ap、lp的乘积正好是每个颗粒平均占有的空间体积，其数值等于颗粒的体积除以（1－ε），即

将方程式（4－13）代入方程式（4－12）可以求得颗粒群松弛时间的倒数值

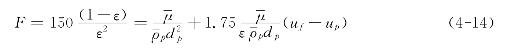
进一步引用方程式（3－50）即可得到阻力系数CD的表达式

式中。将此公式按CD－Re关系画出曲线并与按斯托克斯定律计算小雷诺数下单颗粒阻力系数的公式画出的曲线进行对照（图4－4），可以发现，在ε＝0.917或φ＝1－ε＝0.08时，两个公式画出的曲线可以很好地重合。由此说明，在φ＜0.08时，颗粒群内各颗粒之间的相互影响可以忽略，悬浮体可以按稀相处理。这个情况再次证明在实用中以φ＜0.05～0.08作为划分稀相系统的临界值是正确的。

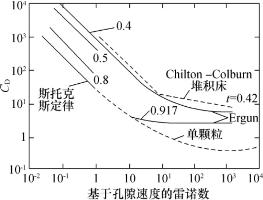
图4－4　单颗粒阻力系数

4.2　气固悬浮体中颗粒受到的其他作用力及单颗粒的运动方程

固体颗粒在气固悬浮体中与流体作相对运动时，除了受到上述流动阻力作用外，还常常会受到其他一系列力的作用。例如：当旋转颗粒在流体中做相对运动时，将受到马格努斯旋转提升力（Magnus spin lift force）的作用；当悬浮系统流场存在较大速度梯度时，颗粒会受到萨夫曼剪切提升力（Saffman shear lift force）的作用；当系统存在压力梯度和温度梯度时，颗粒又会受到压力梯度力（pressure gradient force）和热作用力（thermal force）的作用；另外，在颗粒与流体间作相对变速运动时，颗粒会受到虚拟质量力（virtual mass force）和倍瑟特力（Basset force）的作用，紧靠固体壁面的颗粒还会受到范德华斯力（van der Waals force）的作用。在存在力场条件情况下，颗粒还可能受到重力、电场力或磁场力的作用。

除以上所述作用力外，对于密相气固悬浮系统，其中颗粒还受到颗粒间碰撞与摩擦的相互作用，随着固相浓度的增加，颗粒间的作用力将对颗粒的运动产生重要影响。在采用欧拉方法对气固悬浮系统进行研究时，若颗粒相存在明显不同的粒径分级，则可形成不同颗粒相，不同相颗粒间的碰撞也会引起附加的碰撞阻力，这些力与流动阻力一样都会影响悬浮体内颗粒的运动。

下面将对气固悬浮体运动中颗粒可能受到的其他不同作用力的物理意义和计算方法进行介绍。

4.2.1　马格努斯旋转提升力

在气固两相流动过程中，颗粒间的非对心碰撞会使颗粒产生旋转。在流体流场不均匀的情况下，速度梯度的存在也会使颗粒产生旋转。在低雷诺数下，颗粒的旋转会带动紧靠它表面的流体在其流动方向与旋转方向相同的一侧增加速度而在另一侧降低速度，在该情况发生时，颗粒会受到一个与颗粒运动方向相垂直的力的作用，驱使颗粒向速度较高的一侧移动，这个力称为马格努斯旋转提升力。

Rubinow和Keller给出了旋转球体的马格努斯旋转提升力的计算公式

式中V　→为颗粒与流体的相对速度为球体旋转的角速度为流体的密度；FM的方向与V　→和ω　→所在平面垂直；O（Re）表示未明确写出的级数余数中Re的最低阶数为1。

4.2.2　萨夫曼剪切提升力

Saffman指出，当颗粒所在的流体场存在速度梯度时，即使颗粒不旋转，它也会受到一个升力的作用，这个升力是由粘性流体的剪切作用引起的。Saffman推导了一个小球在无限大的均匀单纯剪切流场内沿流线低速移动且同时旋转时所受到的力的计算公式。分析中使用了三种雷诺数，它们分别为

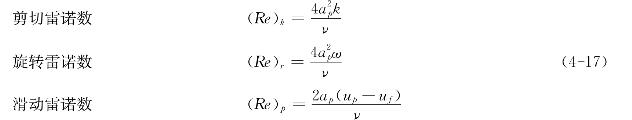
式中（up－uf）是以颗粒中心为基准量测的颗粒相对滑动速度；k是流体横向速度梯度的绝对值；ω为颗粒旋转的角速度。

分析指出，在这种情况下，颗粒受到三个力的作用。第一个是斯托克斯阻力

第二个力是前面提到的因旋转而引起的马格努斯旋转提升力，简化后为

而第三个力就是因滑动和剪切引起的横向力——剪切提升力

上述分析的适用范围为

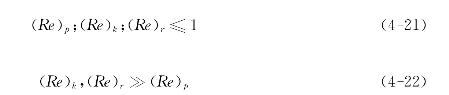
且

对上列各关系式进行比较可以得到斯托克斯阻力、马格努斯旋转提升力和剪切提升力之间的相互关系

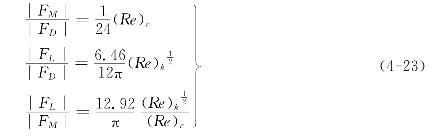
由上式可见，在颗粒直径很小时，由于（Re）r和（Re）k值均很小，相对于斯托克斯阻力，FL和 FM可以忽略。另一方面，我们知道，速度梯度主要存在于边界层内，因此，当颗粒直径大于边界层厚度时，FL和FM也将减少。只有那些颗粒直径稍小于边界层厚度且紧靠壁面的颗粒才能受到较大的剪切提升力。此外，FM的大小在很大程度上取决于颗粒的旋转速度。Saffman认为除非颗粒旋转的角速度大大高于剪切率，即一般情况下马格努斯旋转提升力与剪切提升力相比可以忽略。

4.2.3　压力梯度力

流体存在压力梯度时也会对颗粒产生作用力。其受力情况见图4－5。如图所示，半径为ap的小球上的环形微元表面在压差下受到的作用力为

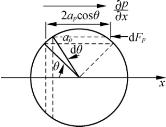
图4－5　压力梯度作用力

积分给出

压力梯度作用力与压力梯度的方向相反。

4.2.4　热作用力

热作用力是由两种原因引起的。一种是由于颗粒周围的流体存在不均匀温度场，冲击颗粒两侧的气体分子具有不同的速度，使颗粒受到热压力——通常称为热泳力（thermophoresis force），在此力作用下颗粒由高温侧向低温侧移动。另一种是当颗粒处于不均匀的热辐射场中时，颗粒受到不同辐射强度的两侧的温度会出现差别，热侧表面上的气体分子离开颗粒表面时将带走比冷侧表面气体分子大的动量（从分子运动论的微观分析，颗粒表面吸附的气体分子与周围气体分子一直在不停地交换），从而对颗粒产生一反作用力，推动颗粒从高热辐射侧向低热辐射侧移动。这个力通常称为光泳力（photophoresis　force）。

Hettner通过分析指出光泳力可按下式计算

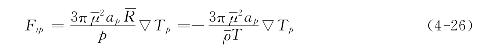
式中p为周围气体压力；T为气体温度为气体常数分别为气体的动力粘度和密度；▽Tp为因热辐射引起的颗粒内部温度梯度，如果颗粒很小，▽Tp将很小，Ftp常常可以忽略。热泳力的最早计算公式则是由Epstein于1929年提出的

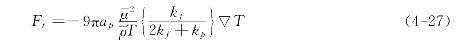
式中T为周围气体的平均温度；kf和kp分别为气体与颗粒材料的导热系数；▽T为周围气体的温度梯度。

实验发现在克努森（Knudsen）数较大时，由上式计算的结果与实验结果相比会出现较大误差，如Kn＝0.1时误差为20%，Kn＝0.2时误差达到50%。这里Λ是气体分子自由程，ap是颗粒半径。

J.R.Brock在对热泳力进行深入研究的基础上把Kn数考虑进去对热泳力的计算公式进行了多次修正，经过他修改的最新的热泳力公式具有如下形式

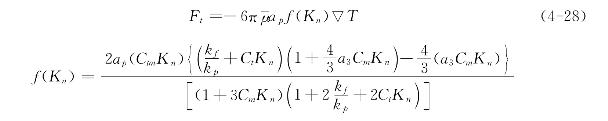
式中Ct为温度跃变系数，Ct＝3.32；Cm为粘性滑动系数，Cm＝1.19；Ctm为热速度系数，Ctm＝0.461；a3为考虑二次滑动的常数，a3＝2.4。

4.2.5　虚拟质量力

当一个颗粒相对于其周围流体加速时，在颗粒周围将产生一个围绕它的二次流动。因此，为了使颗粒运动，除了要消耗使它本身加速所需要的功外，还要额外消耗产生二次流动的功。根据计算，一个半径为ap的球形颗粒在无限大的静止无粘性流体内以加速度运动时，所需要的力为

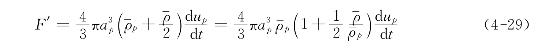
也就是说，颗粒看起来像有一个附加的“虚拟质量”，其数值等于被它排除的流体质量的一半。

对于球形颗粒，当颗粒与流体作相对变速运动时，虚拟质量力可表示为

式中uf为流体速度；up为固体颗粒的速度。

不同形状的颗粒具有不同的“虚拟质量”。作为普遍形式，可以认为，在加速时颗粒的质量以的比率增加。对于球形颗粒；对于长短轴比为2∶1的椭圆颗粒，C＝0.2；当长短轴之比达6∶1时，C值降至0.045。此外，颗粒群C的数值还决定于颗粒的体积含量φ，Zuber建议这时C的数值为：C＝（1＋2φ）/（1－φ）。

对常压下的气固悬浮系统，由于值很小，虚拟质量力只有在颗粒具有很大的加速度时才明显，故一般情况下均可忽视。然而对液固系统以及气固悬浮系统流过喷嘴的情况，此效应必须考虑。

4.2.6　倍瑟特力

当颗粒相对于流体作加速运动时，由于流体的粘性效应，颗粒附近会形成边界层并逐渐增长，其瞬间流场将不仅与当时的条件有关，而且也与在这之前颗粒的运动状态有关。因此，计算中必须有一项专门反映“记忆效应”的特殊项，即倍瑟特（Basset）项。它是由Basset首先考虑的。对于层流，Basset获得由记忆效应引起的附加力——倍瑟特力

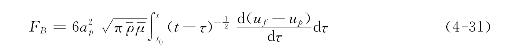
式中τ是一个时间变量，通过它对颗粒从开始加速的时间t0到计算时的t为止的整个运动过程作出积分。对于颗粒群，由于周围颗粒的影响，Zuber建议乘上因子（－1－φ）－2.5。

由式（4－31）可知，FB的数值决定于加速度，只有当颗粒相对于流体的加速度很大时，此力才会明显而必须予以考虑。

4.2.7　范德华斯力

范德华斯力包括分子之间和原子之间除化学结合力以外的所有作用力，对于两个紧密接触的平面之间，此力为

式中S为接触平面的面积，hω为利富希兹－范德华斯（Lifshitz－van　der　Waals）常数，Z0≌4A0（1A0＝10－8　cm）。对于半径为a的球体与平面接触的情况，此力可按下式计算

hω的值随物体材料的不同而不同，一般情况下0.6eV≤hω≤11eV。对于石英与石灰石，hω≌3.6～6.5eV；金属与半导体材料，hω≌2～11eV；合成纤维，hω≌0.6eV。如果相互接触的两个物体由不同材料构成，则其综合hω值为

式中hω11为相互接触的两个物体的材料均为材料1时的hω值；hω22是表示相互接触的两个物体的材料均为材料2时的hω值。随着两物体间的距离增大，范德华斯力很快减弱，当距离大于100A0时，这种粘着力就可以忽略不计。故范德华斯力只存在于紧靠壁面的颗粒与壁面之间以及紧靠在一起的颗粒之间。

4.2.8　场力

气固悬浮系统可能遇到的场力一般包括：重力、离心力、电场力与磁场力等。

重力是人们最熟悉的一种场力，其方向恒指向地心。当颗粒沿与地面垂线Z成θ角的x方向运动时（参见图4－6），重力在x方向及垂直方向y方向的分力分别为

离心力出现于颗粒做曲线运动时

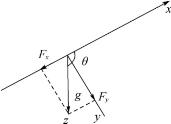
图4－6　重力的分量

这里r为颗粒运动轨迹的曲率半径。

带电颗粒置于电场会受到电场力的作用。两相悬浮系统中的颗粒常会因种种原因而带荷电，即使没有外加电场，带电颗粒群也会因颗粒间的相互作用而存在电场力。

带电荷颗粒间的作用力可用大家熟悉的库仑定律表示。真空中两个分别具有电荷q1和q2的质点在距离为r时的相互作用力可用下式表示

式中K为一系数，当采用CGS单位制时，K＝1；当采用SI单位制时，电荷的单位用库仑（C），距离的单位用米（m），力的单位用牛顿（N），而，这里ε0为真空电容率（permitivity）。这样Fe可表示为

式中E2和E1分别为颗粒2和颗粒1在圆周距离r处的电场强度

如果荷电质点处于电介质中，公式（4－38）和（4－39）中的ε0应该用ε代替，ε称为该介质的电容率或介电系数，该系数通常也可以写成

这里K称为介电常数（dielectric　constant），对于空气，K≌1。

如果颗粒处于外加电场或荷电颗粒群之中，电场力计算公式仍为

但式中E应该用颗粒所处位置的电场强度代替，qp则为该颗粒所带电荷。

根据静电的概念，在一个充满带电颗粒的研究空间内，电场强度、电位和空间电荷间存在着如下关系：

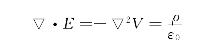
该式称为泊桑（Poisson）方程，式中V为空间各点的电位；ρ为所研究空间中电荷的体积密度，ρ＝qpnp，其中np为单位体积质点数，qp为每个质点的电荷量。

磁场对悬浮颗粒存在作用力出现于两种情况下：一种情况是带电颗粒在磁场中运动，这时颗粒将受到洛伦兹力的作用

按照矢量的定义，F　→B的大小应为

式中qp为颗粒所带电荷量（C），up为颗粒运动速度（m/s），而B则为磁感应强度（T），θ为的夹角的方向与V　→和B　→构成的水平面垂直，参见图4－7。

另一种情况是由铁磁质颗粒构成的悬浮体置于磁场之中。如果外加磁场是均匀磁场，由磁性颗粒组成的整个床层将不会受到任何静电磁场外力作用，但受磁场感应的颗粒群将成链状排列，称为磁链。颗粒与颗粒之间的相互作用力可用下式表示：

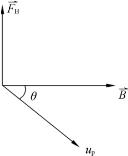
图4－7　洛伦兹力

式中K1为系数，dp为颗粒直径，B为磁感应强度。

如果悬浮体处于非均匀磁场中，假设磁力线是弯曲的，颗粒将以链状沿磁力线呈弯曲排列。由于在径向磁感应强度的密度不同，颗粒之间除相互作用力外，还受到一个指向弯曲中心的力，该力与磁感应强度的梯度和磁场强度的乘积成正比，可表示为

式中K2为系数，H为磁场强度，为沿曲率半径方向的磁感应强度梯度。

4.2.9　碰撞阻力

前面已经提到，当流体中存在颗粒直径明显不同的两组或多组颗粒群时，应把各组颗粒群看作不同的相处理。不同相间颗粒的相互碰撞会给每一个颗粒群（相）带来附加的碰撞阻力。现以一个颗粒相中的某一个颗粒（s）为例，分析它因受另一颗粒群（R）的碰撞而受到的阻力。

在开始分析前，先考察两个颗粒（s）和（r）作弹性碰撞时的受力与运动情况。

如果碰撞时颗粒（s）固定不动，碰撞力可按颗粒（r）碰撞前后的速度变化借助颗粒运动方程计算

式中为碰撞时颗粒（r）的速度变化率。

如果颗粒（s）也在运动（参见图4－8），则按两个颗粒所受碰撞力大小相同，方向相反的原则不难推得，这时的碰撞力应为

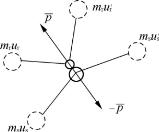
图4－8　两个颗粒的碰撞

式中称为两个碰撞颗粒的“折合质量”，称为两个颗粒的相对速度。由式可见，当两个具有不同质量和速度的颗粒相碰时，碰撞作用力的计算公式可直接套用公式（4－46）。但公式中的质量mr和速度u→r应分别用“折合质量＂”及相对速度u　代替。

下面让我们来分析颗粒（s）与颗粒群（R）的碰撞情况。为了方便起见，先假定颗粒（s）不动，颗粒群（R）则以up的速度平行冲向它的表面。观察其中的一个颗粒，其质量为mr，以碰撞角θ冲到颗粒（s）的表面（参见图4－9）。为了简化，再假定颗粒间的碰撞为弹性碰撞，且颗粒（r）对颗粒（s）仅作单次散射碰撞［即经一次碰撞后的有限时间内颗粒（r）不再返回作另一次碰撞］。根据镜面反射原理，可以求得碰撞前后颗粒（r）在up方向上的动量变化率

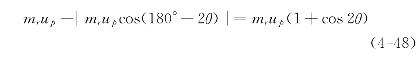
此值也是颗粒（r）对颗粒（s）的碰撞作用力在up方向的分量。这样，颗粒群（R）作用于颗粒（s）的碰撞力可以表示为

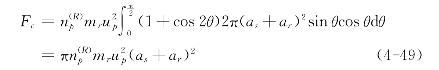
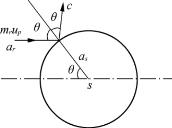
图4－9　颗粒（r）冲撞固定颗粒（s）

式中为悬浮体中颗粒群（R）的数量密度；as和ar分别为颗粒（s）和颗粒（r）的半径。

考虑实际情况，由于颗粒（s）附近流体的绕流运动以及颗粒（r）的惯性，颗粒群（R）冲向颗粒（s）时的实际运动轨迹并不是平行的（参见图4－10），只有那些处于以半径a′构成的圆形截面内的颗粒（r）才能与颗粒（s）相碰。人们把这个面积π（a′）2与颗粒（s）的截面积之比用η表示，称为碰撞份额。η值的大小与一系列因素有关，通常将这些因素归集于两个无因次参量φ和φ，并表示为

这里φ称为惯性参量，表示颗粒（r）在气流中运动的松弛时间与该颗粒通过颗粒（s）的时间之比，在颗粒（s）不动的情况下

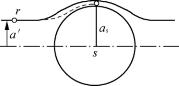
图4－10　考虑颗粒（r）惯性的碰撞情况

式中u0为远离颗粒（s）处的气流速度。

考虑上述情况，公式（4－49）的等号右侧应乘上碰撞份额η。

对于颗粒（s）与颗粒群（R）同时运动但速度不同的情况，正如前面的分析，碰撞作用力计算公式（4－49）可引申使用，但公式中的mr与up应分别用代替。与此同时，参数φ和φ也应作相应改变，这时

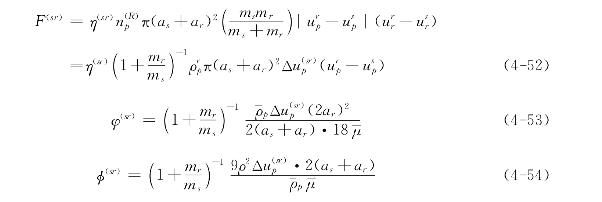
Soo建议η（sr）与φ（sr）和φ（sr）间的关系可用下式表示

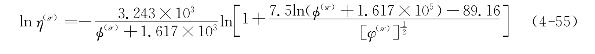
与颗粒在流体中运动时的粘性阻力相似，颗粒（s）受颗粒群（R）碰撞时的阻力也可表示为为因颗粒（r）碰撞而使颗粒（s）变速的松弛时间的倒数。的表达式可通过下式求取

式中ms为颗粒（s）的质量。利用公式（4－52）不难给出

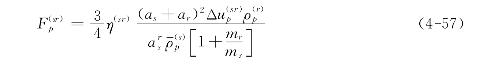
对于给定容积内的两组颗粒群，由作用力与反作用力相等可以推得

由此得出

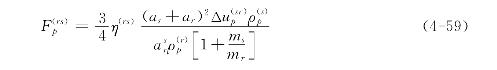
4.2.10　单颗粒在气流中的运动方程

知道了上述各项颗粒所受到的各种作用力，即可列出颗粒与流体作动量交换的普通方程

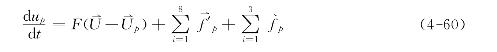
式中为颗粒相单位质量力因重力场、电场或磁场作用而受到的力，

为颗粒相除场力外，因碰撞、加速、流体剪切等受到的8种力。

需要说明的是，在实际工作中公式（4－60）所列的3种场力和8种其他作用力常常不会同时出现。例如，范德华斯力仅出现于紧靠固体壁面处，因此此力只需放入边界条件而不必列入颗粒的运动方程；压力梯度力、虚拟质量力和倍瑟特力只有在悬浮体通过冲击波或喷嘴时才明显，平时可以忽视。其结果是，对于每一种具体情况，公式（4－60）中必须放入的作用力项并不多。显然，这对简化计算是有利的。

关于颗粒间的碰撞作用力，将在本书的第6章进行详细介绍。