将一个正方形在角上切去1/4,所剩下的图形能不能分割成恒等的四块?(所谓恒等就是有相同的形状,面积也相等)答案是可能的,正如下图左所示。
与此相仿,把一个等边三角形的顶上切去1/4,剩下来的图形也可能分割成恒等的四块,如下图中所示。
下图右所示是一个正方形,可不可能分割成五个恒等的图形呢?

该题中的小岛位于图中的那样的正方形湖的中心,一个人想从湖边走到小岛上去,他不会游泳。湖边有两块同样的跳板,但每块跳板的长度要从湖边搭到岛上是略短了一些。这个人将如何利用这两块跳板走到小岛上去呢?

下图中的桥,乍一看这种结构是没有可能搭出来的,因为桥的重心是极其不稳的。可是如果有正确的方法,一样可以搭成这座看似不可能搭成的桥。
用几块积木,你能否搭出这样的桥呢?

下面这两个图形都是由七巧板拼成的,只是左边的那个图形比右边的多出一块来,这么看似乎是不合理的,不过它们确实是由同一组七巧板拼成的,你能做到吗?

小明有两个兄弟,他们三兄弟分别住在三个互不相通的房间,每个房间门上都有两把钥匙。
请问:如何安排房间的钥匙才能保证小明三兄弟随时都能进入每个房间?
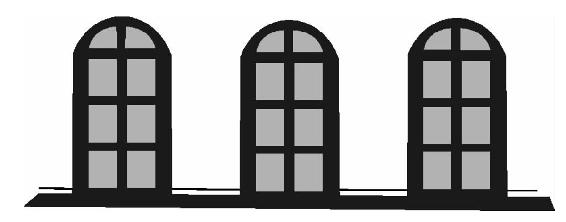
如图所示,有一个容量为2公升的正方形量具。现在要求使用这个量具准确地量制1公升的水来。该怎样度量呢?

单摆一直吸引着科学家们,一个制作精良的单摆可以精确计时,可以测量引力,也可以感知相对运动。
将两个摆长相等,但摆球质量不同的单摆同时释放,其中将较重的那个摆球从较高的高度释放。哪个先摆过一周?
如图所示,用八根木棍组成两个正方形,其中一个正方形的边长为8厘米;另一个正方形的边长为4厘米。现在要求打乱这个正方形,重新用八根木棍正好构成三个面积相等的正方形。

问:应该怎么构制?
5+5怎么会等于5呢?知错就要改。移动其中的三根火柴,就能将它改正确。你不妨试试看?

人的大脑细胞的总数超过300亿个,这些脑细胞构成的网络比全世界的电话网络的联系还要复杂。要体会一下大脑网络运作的感觉吗?
请看下图。从起点到终点共有多少种不同的路径?

你只能从左到右,不能倒退,即到达一个节点,或者朝上前进,或者朝下前进。
这类题目,看来是纯粹操作性的,其实是分析性的。你应当在尝试具体的路径之前,进行思考和分析,然后设法找到一种简单明了、一目了然的方法。
如图所示,有一个魔术方阵,其纵向、横向、斜向相加之和,均等于15。现在要求做一个纵向、横向、斜向相加之和均等于16的魔术方阵,而且方阵中的数字也全不相同。
应该怎样设计呢?
下面一个4×4方阵,我们称它为完全四次方阵。因为它除了每行、每列和每条对角线上四个数之和都等于34外,还有一些奇妙的性质。仔细观察一下,你发现了什么?

每一种物体从不同的角度都呈现不同的形状,这很奇妙。不管你信不信,图中的10个由立方体组成的形状中,3种形状出现了2次,1种形状出现了3次,1种形状出现了1次。你可能需要一些时间把它们分类。
你能找出这5种不同的形状吗?

下图是由18根火柴拼成的6个“三”,但如果在每个“三”字上添上3根火柴,它就会变成6个汉字。试试吧,这个太容易了!

下面7个图形中,有一个和其他6个不同。是哪一个呢?为什么?

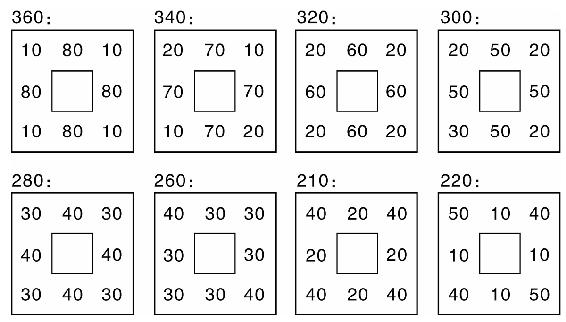
在古代的一次城市保卫战中,一位将军带领360个将士守护一座城池。这位将军将360个将士分派在四面城墙上,并使四周敌人都能看到每边城墙上有100个将士守卫。战斗异常激烈,守城将士不断阵亡,兵员逐渐减少至340、320、300、280、260、240、220。但在这位将军的巧妙安排下,每边城墙上的守卫将士始终都能让敌人看到有100名。敌人以为是天帮神助,便惊慌地后撤了。
问:这位将军是怎样巧妙安排的呢?
在桌子上放三只杯子,如图所示。你的目标是要让全部三只杯子口朝上放着,要求只能翻三次且每次同时翻两只杯子。你试一下就知道,这很容易的。

现在,仍按上面的方法,让我们试一试能不能将桌子上的六只杯子全部口朝上?或口朝下呢?

用18根火柴组成9个全等的三角形,如果分别拿掉1、2……5根,就会依次变成8、7……4个全等的三角形。开动你的大脑,发挥你的想象,你肯定能做到!

如图所示,用八枚硬币组成一个L图形。

问:如何能在只移动一枚硬币的情况下,使这个图形竖行与横行的硬币数均为五枚?
有车就会有停车的麻烦。有一个如图所示形状的车库,在这样的状况下,下面的车1、2、3、4(分别停在I、J、K、L上)要和上面的车5、6、7、8(分别停在A、B、C、D上)正好互换位置,最低要移动多少次。
需要说明的是,一个框子里只能装下一台车,所谓下面的车和上面的车“正好互换位置”,指的是1与5、2与6、3与7、4与8互换。
把图中10面双面镜旋转90度,你就能从右上角的观察孔中看到左下角的灯泡。你知道应该转动哪10面镜子吗?

在一个表格里有几只兔子,每只兔子都有一棵专属于自己的胡萝卜,这棵胡萝卜有可能紧邻在兔子的四周,但不可能出现在兔子的对角线相邻位置。同时,两棵胡萝卜也不能相邻,也就是说,它们彼此之间不能“接触”。位于每行和每列的胡萝卜数目已经标示在表格旁了,到底兔子们的食物在哪里?

下面是一个7×7的纵横图,人们叫它同心方阵。你能不能说出这一方阵的特点?

有如图的三组木板,要分别把它们拼装成最简单形状的桌面,请问应该怎样设计拼装为好?

图1

图2

图3
按照图中给定的尺寸,看你最快能用多长时间算出从A角到B角的长方形对角线的长度?(每小格为1厘米)

想在三个村庄之间用最经济的方法建立起连接它们的公路。你能找到一种一般化的方法吗?
为了把这个问题弄得更清楚,请观察下面的两个三角形,如何在三角形中找到一个点,使它到三个顶点的距离之和最小?
某公司运来了一批没有盖子的立方体纸盒,他们都是由四个侧面和一个底面组成的,而且是同样大小。由于仓库的容量有限,这批空盒子很占地方,于是老板决定把他们沿着某几条棱剪开,展成可以平铺但仍连成一片的纸板,以节约堆放的空间。于是老板找来工人,让他们尽快完成这个工作。
没过多久,工人们就把工作完成了,可老板发现他们剪成的纸板堆放在一起很不整齐,仔细一看原来纸板展开的式样彼此不同。
请问你知道纸盒能剪成多少个不同的样式吗?
哥尼斯堡这座城市有两个岛屿(如图所示的A和B),及连接它们的七座桥。岛与河岸之间架有六座桥,另一座桥则连接着两个岛。当时,居民们有一项普遍喜爱的消遣,就是在一次行走中跨过全部七座桥而不许重复经过任何一座桥,但是没有人成功。请问,有没有一种可能在一次行走中走过全部七座桥而不重复经过任何一座?
将从1到16的数字填入下图中的16个方格内,使得每一行、每一列以及两条对角线上的和相等,且和为34。

有大小相同的6块正方形的布叠放在一起后如下图。请问:这些布由里至外是依照什么顺序叠放的呢?选出正确的答案。
A.3→1→5→4→2→6
B.4→1→3→5→2→6
C.1→3→4→5→6→2
D.1→3→4→5→2→6

下列5个图形中,有4个图形两两对应,那么,余下的一个图形是A、B、C、D、E中的哪一个?

请仔细观察下面的5个图,然后找出这些图形中与众不同的那一个图形。

A~D四个立方体中,哪一个和上面的一模一样?

下面四个所给的选项中,哪一选项的盒子不能由左边给定的图形做成?

小明用下图甲的胶滚沿着从左到右的方向将图案滚涂到墙上,右边所给的四个图案中符合胶滚滚涂图案的是哪一个?
可以。
此题实际上非常简单。如果你不能迅速正确地把正方形进行分割,可能是受了前两个图形的影响,你一定相当费力地仔细分割而难得要领。将正方形分割成五个恒等的图形唯一的答案如图所示。

下面的图1给出了两块木板搭成桥的答案。
图2则是用三块木板搭成的桥。
接下来,或许不难想象,如何用五块或者八块长度更短的跳板仍能跨过湖面。

图1

图2
如下图,只要在搭建开始时多放两块作桥墩,当搭好后桥的结构稳定了,这时就可以把多余的桥墩撤走了。


把三个房间命名为甲、乙、丙,小明三兄弟分别拿一个房间的钥匙,再把剩下的钥匙这样安排:甲房内挂乙房的钥匙,乙房内挂丙房的钥匙,丙房内挂甲房的钥匙。这样,无论谁先到家,都能凭着自己掌握的一把钥匙进入三个房间。
如图所示,把量具倾斜,或者使量具的两个顶角与另两个底角处于同一个水平面上。此时所度量的水的体积正好是1公升。
两个摆的周期完全相同。这似乎很难想象,但单摆的摆动周期仅仅取决于其摆长。无论摆动幅度有多大,周期都是一样的。
单摆运动的奇特方式遵循如下规则:
1.摆动周期与摆球的质量无关;
2.摆动周期与摆球幅度无关;
3.摆动周期与摆长的平方根成正比。
如图所示。将a、b、c、d四个木棍对折。
你可以采取如下方法进行思考和分析。
设法在每个圆圈内写上一个数字,这个数字表示到达这个圆圈所有可能的路径数目。显然,左边起点的圆圈内的数字是1。不难理解,其他的每个圆圈内的数字,等于其左侧与它直接相连的圆圈内的数字之和。这样就可以在每个圆圈内填上确定的数字。
例如,每个填写有数字1的圆圈的左侧都只与唯一的一个圆圈直接相连,该圆圈内的数字是1;填有数字2的圆圈的左侧与两个圆圈直接相连,这两个圆圈内的数字分别都是1;等等。这样,作为终点的最右侧圆圈内的数字就是20。这说明共有20种不同的路径。

如图所示,只在原方阵中各格数字后再添加 即可。
即可。

①如下图所示的对角线上4个数的和也等于34,如下图,8+5+9+12=11+13+4+6=14+2+3+15=34。

②从图中任意取出2×2的小正方形,它们4个数的和也是34。如:

③从图中任意取出3×3的小正方形,它的4个角上4个数的和也等于34。如:
出现两次的是1-8、4-10和5-7;出现三次的是2-3-9;6出现一次。

标号为4的图形是唯一一个不是正多边形的图形:其边和角不都相同。
如图所示。
无论怎么试都会挫败的。那是因为一次翻两只杯子将使口朝上的杯子数目增减2或0。第一步时口朝上的杯子数目是1,所以加上2就变成3。第二次一开始口朝上的杯子数目是0,每次翻两只杯子使口朝上的杯子数在0和2之间变,但你永远无法让三只杯子口都朝上。换句话说,第一次口朝上的杯子数是奇数,而第二次口朝上的杯子数是偶数。无论哪种情况,一次翻两只杯子都不会改变奇偶性。
同样,六只杯子也如此,一开始奇偶性为奇,偶数不会改变奇偶性。所以,口都朝上和口都朝下的结局也是不可能的。

将L图形竖行最上端的那枚硬币移放到L图形竖行与横行交点的那枚硬币上(以黑点表示),即可达到要求。

最低需要移动43次。只要认真地按下表的顺序移动,就可以换成位置。

这里给出了一种方法。



横排、竖列、对角线上的各数字之和相等。
第一组图形的拼装比较容易,凭借第一感觉就能做到。只要将其中的一块木板翻转就可以了。

问题是在第一组图形拼装好以后,思维很容易在第一组图形的拼装顺序基础上继续向前滑行。将第二组图形拼装成如下形状:

这种形状虽然也可以称得上是“简单”,但还不应算是“最简单形状”。
如果思维满足于第二种拼装,无形中会加剧思维单一的惯性,从而不再改变对事物结构的认识,让思维继续向前滑行,用既定的思路认识第三组图形,从而更加剧了原有思维的框架,将第三组图形拼装成如下形状:
如果说第二组图形还能够称作简单图形,可以当桌子用,那么,第三组图形就不能称其为“桌子”了。
正确答案应按以下方法拼装。

图1
图2
图3
画出长方形的另一条对角线,你立即会看出它是圆的半径。长方形的两条对角线总是相等的,因此从A角到B角的对角线长度等于圆的半径,为10厘米。
这两个问题是相关的,因为无论三个村庄在什么位置,都可以把它们看作三角形的三个顶点。无论对村庄或三角形,我们都要求到三个顶点距离和最短的那个点。
在三角形的三个角都小于120度时,只要在三角形中找一点,其到任意两顶点的连线的夹角都是120度,如图。
对于有一个角大于120度的三角形,最短路径经过构成这个角的顶点。


如图,设这个没有盖子的立方体纸盒为ABCD-A′B′C′D′,其中各侧面ABB′A′、BCC′B′、CDD′C′、DAA′D′分别简记为Ⅰ、Ⅱ、ⅠⅡ、Ⅳ,底面ABCD则简记为底。现在要把他展平,于是总要剪开几条棱。我们把着眼点放在底面ABCD周围的四条棱AB、BC、CD、DA上。
首先,如果这四条棱一条也不被剪开,那么只有把四条侧棱AA′BB′、CC′、DD′都剪开才能把这个纸盒子展平。展成图为下图。

如果四条棱中仅一条被剪开,不妨设AB被剪开,则须在AA′、BB′中选一条剪开。但这样只是把侧面ABB′A′像门一样的打开了。要把这个纸盒展平,还必须剪开CC′和DD′这两条侧棱。展开的样式如下图。其中左边是剪开AA′的样式,右边是剪开BB′的样式。但因为这两种样式呈镜像对称,所以应算作同一种。

如果四条棱有两条被剪开,那么就会有以下两种情况:
第一种是剪开的两条棱是相邻的。设这两条棱为AB和BC,那么可剪开BB′和DD′,展成如下图左边的样式;也可以剪开CC′和DD′,展成的如下边中间的样式,也可以剪开AA′和DD′展开图形为下边右边的样式。但因为后两种样式呈镜像对称,所以应算作同一种。

第二种是剪开的两条棱是不相邻的。设这两条棱为AB和CD,那么可剪开BB′和CC′,可剪开AA′和DD′,可剪开AA′和CC′,也可剪开BB′和DD′。前两种剪法展成的样式可在平面内通过1800旋转相互变换;后两种剪法展成的样式则呈镜像对称。因此只能算两种样式,如下图。

如果四条棱中有三条被剪开,那么必须在四条棱中剪开一条而且仅剪开一条,才能把这纸盒展开。这样就有四种剪法,导致四种样式,但其中两两成对,互相为镜像对称,因此只能算作两种。如图。
所以,最后结果是可以展成8种不同的样式。
只通过一次是不可能的。
这道题看上去好像是简单的事情,结果却被证明为非常复杂。七桥问题直到瑞士数学家欧拉才得到解决。当欧拉第一次听说它并对它感兴趣时,他就着手证明它不可能有解。欧拉解决这一问题用的是今天人们称之为网络的拓扑学知识。
一个网络基本上可以看成是一个问题的图样。哥尼斯堡七桥问题的网络可以图解如下:

网络是由一些线一些点连接起而成。初看起来,上图也许不像前面的图,但是用数学术语的话,它们是完全等价的。这就是说,它们是拓扑等价的。
标明A、B、C、D的点分别代表河的北南两岸(C和D)和两个岛(A和B)。线代表将ABCD连接起来的路或桥。两座桥连接C和B,两座连接B和D,一座连接A和B,一座连接A和C,一座连接A和D。欧拉把一个点或结点描述为“奇”的或“偶”的。如果出自一个结点的线的数目是奇数,这结点就是奇的,如果线的数目是偶数,这结点就是偶的。欧拉不仅研究了哥尼斯堡桥,还研究了许多别的网络,结果证明:
要走完一条路线而其中一段行程只许经过一次,只有当奇结点是0或2时才是可能的。在所有其他情况下,如果不走回头路,就不能历遍整个网络。
他还发现,如果有两个奇结点,那么经过整个路线的路必须从一个奇结点开始,到另一个奇结点为止。哥尼斯堡难题终于有了解法。
哥尼斯堡七桥问题成为拓扑学的起源。在俄罗斯的一个地区,称为加里宁格勒州,过去叫哥尼斯堡,这座美丽的普鲁士城因为数学新领域——拓扑学的图论而著名。
解法很多,图示一种。

正确的顺序是D,即1→3→4→5→2→6。
E。A是C的映像,B是D的映像,剩下的是E。
E。这5个图形中只有它左右颜色不对称。
B。
C。由左边图形可以看到,带对角线的两个面是相对面,不可能相邻,因此C项不符合要求。
C。观察胶滚上的三个三角形的分布状况可以知道,胶滚从左往右滚,最先接触到墙壁的是中间的三角形,当中间的三角形的对称轴接触到墙面时,其他两个三角形同时开始接触墙面,据此,
选C。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















