从代数结构的观点来看数的推广

伽罗华的工作成就是具有划时代意义的。伽罗华对数学做出的贡献远不是解决了代数方程求解问题，比这更为重要的是他在研究五次方程根式解的问题时，引进了许多新概念，开辟了代数学的一个崭新领域——群论。利用群的性质，伽罗华完全、彻底地解决了几个世纪以来数学家们一直未能解决的五次及五次以上代数方程根式解问题，给出了非常漂亮的判定准则。从此后，代数学的发展有了全新的研究对象：群。

随着20世纪初集合论的普及与公理化方法的发展，人们给出了抽象群的科学表述。现在公认群是元素间存在一种运算且满足下列四条公理的集合。

1°（封闭性）对都有

3°（单位元）对使

4°（逆元）对使

先提一点：这里为了形式简捷，我们引入了两个数学符号。一个是，它表示“任意”；一个是，它表示“存在”。它们在后面还要用到。

下面我们再对上述定义做几点说明：

1.只满足第一、二条的结构叫半群。

2.对于首次接触群概念的读者来说，运算这一概念，可以理解为对两个或多个数学对象运用某种法则而得到第三个对象的一个过程。群中所使用的运算是任意的。它叫什么名称，或者用什么符号来表示都是无关紧要的，上面我们使用×表示这种运算，只是一种习惯而已。同样地，上面的单位元采用的符号1，也只是一种习惯，并不代表我们所熟知的自然数1。对于不同的群而言，单位元其实是极不相同的。

3.半群、群既不是数也不是形，而是更加抽象的概念。从数学上来说，一个半群或群是一些元素组成的一个集合，这些元素可以使用某种运算（如加法或乘法）结合起来，并且这种运算满足某些条件。上述第一条封闭性概括了群的一个重要性质：当它的任何两个元素用这种运算结合时，其结果仍是群中的一个元素。

4.群依照不同的特点又可以划分为不同的类型。如按运算是否可交换，可以将群划分为不可换群与可换群。后者又称为阿贝尔群。

读到这里，很多读者可能已感到些茫然了，他们会迷惑地问：半群、群、阿贝尔群这一些到底说的是什么东西呢？对于初次接触这种抽象概念的读者产生这种疑问是极其正常的。下面我们通过几个简单例子说明一下上述的几个概念。

从小学时我们就明白了一个道理：任意两个自然数的和仍然是自然数，用现在的话说就是自然数关于加法具有封闭性。并且很显然的，对任意的三个自然数a，b，c来说，都成立（a＋b）＋c＝a＋（b＋c），即满足加法的结合律。因而按照上述的定义，我们可以说自然数集在通常意义的“加法”运算下构成一个半群。对此我们可以简单记作＜N，＋＞是半群，其中N代表了自然数集。同样地，不难验证，自然数在通常意义的“乘法”运算下也构成半群，即也是半群。

那么，自然数集关于这两种运算是否构成一个群呢？

让我们看一下自然数关于乘法运算，即＜N，×＞是不是群吧！

先来看看它是否满足关于群的定义的第三条。在群中要存在单位元。那么什么是单位元呢？其实单位元是一个极为特殊的元素，它具备性质：集合中的任何元素与它进行给定的运算时，结果都没有发生变化。在自然数中，有没有一个数有这种性质，即任意自然数乘上它都不变呢？1！反应快的读者可能已脱口而出了。对极了！于是我们需要看＜N，×＞是否满足群定义的第四条了，即：在群中每个元素都有逆元。所谓一个元素a的逆元就是指它与a的运算结果要恰好等于单位元，由于在中单位元是1，于是就意味着元素与它的逆元的乘积结果为1。这一点能否做到呢？“取倒数就行”！当然了，任意一个自然数与它的倒数乘积为1是正确无误的，但是问题在于自然数的倒数已经不是自然数了。简言之，像2在＜N，×＞中就不存在逆元。

通过上述讨论，我们可以得出结论了：＜N，×＞不能构成群。不过，原因似乎在于自然数集太小了点，如果我们把集合扩展到正分数又如何呢？

任意两个正分数的积仍然是正分数，满足封闭性；结合性是显然的；存在单位元1；任意一个正分数都存在它的倒数作为它的逆元。于是，正分数关于乘法运算构成一个群。

从这一点上我们可以看出，把数从自然数扩展到分数，数系的结构也随之发生了变化。自然数关于乘法只能构成半群，而分数关于乘法就能够构成群了，扩大后的数系具有了更好的结构。

让我们再看看自然数关于加法运算的情况。前面我们已经知道＜N，×＞构成半群，那么它能否构成一个群呢？

通过类似的讨论，可以发现也不行。因为在这种运算下，元素都不存在逆元，或者用更通俗的说法是自然数关于加法这种正运算是行得通的，但关于其逆运算却不再行得通了。但是如果在自然数基础上添加0与负整数，得到整数集后又如何呢？

一个整数和另一个整数在加法运算下得出第三个整数。在加法运算下所有可能的结果仍是整数，因此我们说：“整数在加法下是封闭的”。至于结合律是显然成立的。整数关于加法运算存在单位元是零。任意整数存在它的相反数作为它的逆元。因此，整数在加法下满足上述四条公理。我们说：整数在加法运算下构成一个群。又由于整数关于加法满足交换律，所以整数关于加法是一个阿贝尔群。你看，在数系沿着这条路扩展后，我们也有了更加丰富的结构。

通过这一通长篇大论式的说明，你是否能够明白半群、群、阿贝尔群代表什么意思了呢？如果你的答案是肯定的，那么我们就要继续前行了。群论建立后，人们又逐渐提出更多的代数系统。于是在前行的道路上，我们马上就遭遇到更为复杂的几个概念。你有啃动硬骨头的信心吗？不妨试试吧！

先去看看“环”是怎么回事吧。

定义一个具有两种二元运算（＋，×）的集合R为环，满足以下八条公理：

1°（加法封闭性）若a、b∈R，则a＋b∈R；

2°（加法结合律）若a、b、c∈R，则（a＋b）＋c＝a＋（b＋c）；

3°（加法交换律）若a、b∈R，则a＋b＝b＋a

4°（加法单位元或零元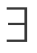）0∈R，使a∈R，有a＋0＝a；

6°（乘法封闭性）若a、b∈R，则a×b∈R，b×a∈R；

7°（乘法结合律）若a、b∈R，则（a×b）×c＝a×（b×c）；

8°（分配律）若a，b，c∈R，则a×（b＋c）＝a×b＋a×c，（b＋c）×a＝b×a＋c×a。

对于这个定义我们说明几点：

第一，首先应该搞明白的一点是群是一个集合关于一种运算得出的结构；而环则是一个集合关于两种运算得出的结构。如同群中我们已经指出的那样，运算符号采用“＋”与“×”只是一种习惯，实际上它们可以代表任意两种运算。

第二，公理1～5是刻画了集合关于加法运算满足的性质，并且不难发现集合关于加法构成阿贝尔群。公理6～7则是刻画了集合关于另一种乘法运算所满足的性质，并且也不难发现集合关于乘法构成半群。而公理8°则刻画了两种运算之间的关系。

第三，环在加法运算下构成一个阿贝尔群，也称加群。加群中的单位元，又常称为环的零元，用0来表示，只是你要搞明白这只是一个代表符号，并不意味着环中的零元总是我们所熟知的数零。加群中每个元素的逆元常称为环的负元。

在又引入了一系列抽象概念后，恐怕读者一时很难消化得了。让我们再通过我们所熟悉的数系的例子来说明一下。

先来看自然数集合在加法与乘法两种运算下，即＜N，＋，×＞能否构成环或域。

前面我们已经说过，自然数关于加法不能构成群，因而＜N，＋，×＞不能构成环或域。

再来看看整数集（通常用字母Z来表示）在加法与乘法两种运算下，即又怎么样呢？

前面我们已经说明过，整数Z关于加法运算构成群，整数Z关于乘法运算构成半群，又整数的加法与乘法运算两者间显然满足分配律。因而我们说＜Z，＋，×＞构成环。事实上，环的结构正是从整数的集合推广而来的。

再来看看＜Z，＋，×＞能否构成域吧。

整数Z关于加法运算构成群，但整数Z关于乘法运算却无法构成群，因而＜Z，＋，×＞无法构成域。那么把数系的范围扩展一下，扩展到有理数集又如何呢？即＜Q，＋，×＞能否构成一个域呢？

由于有理数集关于加法运算构成群，而且有理数集在乘法运算下，只要每个非零元素也都有逆元，因而有理数集（去掉零）关于乘法运算也能构成群；又有理数的加法与乘法两种运算满足分配律，因而＜Q，＋，×＞构成了一个域。可见，在数系扩展到有理数范围后，我们得到了一种具有更好性质的结构：域。在域中加减乘除都行得通，换句话说可以很好地进行代数运算。

事实上，可以证明有理数集是最小的数域。如果从有理数域出发，而θ是一个n次代数数，则θ自身及有理数在四种运算之下结合起来所形成的集合也是n次域。这个域也可以说成是包含有理数和θ的最小域。它也称为有理数的扩域。

实数系添加虚数单位i，可以扩充到复数，复数也组成一个域。在复数域中，有了代数封闭性，可是这个域与实数域相比较，最大的区别之一在于复数域不是有序的。即任意两个复数间不一定能比较大小了。实数的有序性被破坏了，这样我们只好求助于绝对值或范数来弥补这个缺陷。

复数扩展到四元数后，又如何呢？由于四元数的乘法不满足交换律，因而四元数不是一个域。当然，如果我们把域的定义放宽，去掉乘法满足交换律的条件，那么我们可以说四元数是一个非交换域，而此前的有理数域、实数域、复数域都是交换域。

当数系再进一步推广的时候，有着更多的性质丧失了，如有的不再满足乘法交换律。有的甚至不再满足乘法结合律等等。与之相关的，它们的结构也就相应地发生了改变。

从接近20世纪末的角度来看，可以把数系的结构从上到下组织起来：

四元数是非交换域；

复数是无序的域；

实数系是唯一的完备有序域；

有理数系是R的最小子域；

整数系Z是R中包含乘法单位元的最小环；

自然数系N是R中包含乘法单位元且在加法下封闭的最小子集。

这些简洁陈述所代表的精干的思想包括了许多关于结构的信息，确定了不同数系的结构。对于这些深刻的结构原理给予适当的关注是必要的。它使我们能够更加深刻地理解不同数系的相同与相异之处。从结构的观点对数系差别的分析（从最简单的差别一直到最细微的差别）有助于培养人们对数和数系本质的洞察力。

最后需要指明的几点。

其一，以群、环、域这些抽象对象为研究内容产生了一门新的学科，叫抽象代数。它是在19世纪末、20世纪初发展起来的，也有人称之为近世代数。而群、域、环作为极为抽象的代数结构，人们对它们的认识也都经历了一个逐渐的不断深入的过程。

如群的概念。我们虽然说整数加法可以成为一个群的简单并且典型的例证。但是真正群的概念并非是从它得到的。实际上，群的概念长期隐藏在许多对象背后，是形的对称性的抽象结果。事实上，在很长一段时期，人们只停留在具体群的研究，比如置换群、运动群等变换群，那么，能否将各种具体的群的共同特征再抽象出来呢？古典代数学不正是排除符号所表示的具体内容，而只考虑能满足一定运算规则的抽象符号吗？在经过英国数学家凯莱、挪威数学家李等许多人的努力后，抽象群的概念才应运而生。

再如域的概念在伽罗华的著作中就已包含了。数学家戴德金、克罗内克等人也曾从不同角度引入了一些具体的域。而域的公理体系是在1903年由美国两位数学家建立起来的。

再如环的概念，最初是在19世纪末戴德金研究代数数时引进的。克罗内克的论文中也出现了环的概念。但关于环的抽象理论却是在20世纪建立的。尤其是环的系统理论开始于德国数学家诺特。这是一位为环论作出重要贡献的伟大女性。她在前人工作成果的基础上，利用她超凡的抽象方法给出了环和理想的系统理论，把抽象代数的研究工作推向了新的高潮。她最深刻的研究完成于1926年，一般认为抽象代数形成的时间也就是1926年。虽然，诺特之后抽象代数有了长足的进展，但是人们常常从她的工作成果中汲取营养，所以诺特成为当之无愧的抽象代数奠基人之一。

其二，抽象代数的建立过程表明，我们不应该把这些抽象的数学概念归于创造没有鲜明目标的新抽象概念的数学家的想象力，事实上在几乎所有情形下，这些抽象结构的出现都是基于成功攻克从经典数学继承下来的问题的需要。

其三，结构数学的兴起，代表了人们对一种新的观念的认同：在一种数学理论中，起着根本作用的是所涉及的数学对象间的关系，而不是这些对象的本性；因此在两个很不相同的理论中，却可能用相同的方式表述两者各自的关系，这些关系及其提供方便的系统形成一个隐藏在这两种理论深处的同一结构。随着科学的发展，这种从代数中研究运算结构开始的观点在数学中也不断取得进展。20世纪初，E·V·亨丁顿为群等代数结构作了一般的公理化处理。1930～1931年，诺特的学生，荷兰数学家范·德·瓦尔登出版《代数学》，成为抽象代数的经典之作，也使抽象代数成为现代的基础。在这本书中它完成了代数领域系统公理化工作，他在序言中说：抽象的、形式化的或公理化的方向在代数领域中造成了新的增长，特别地在群论、域论、赋值论和超复数等等部门中引起了一系列新概念的形成，建立了许多新的联系，并导致了一系列深远的结果。

其四，也许有许多读者会问：如此抽象的概念是否真有应用价值呢？想想看，伽罗华引入群论的过程中不是已经给出了群这一抽象概念应用的典型例子了吗？事实上，由于群、环、域等代数系统在数学中的广泛出现，又由于各种理论与应用中出现的问题，最后往往归结为某种代数系统的研究，代数系统的一般理论发展成了分支繁多（如群论、环论等）的代数类数学，它已成为整个数学最基本的工具之一。因而，以研究代数结构以及不同代数结构之间关系的抽象代数被誉为“数学的提纲挈领的钥匙”，它的方法和结论也渗入到各个不同的数学分支中，同时人们还发现这种抽象的数学领域常常具有深刻的实际应用价值。如这些抽象结构现在已成为研究计算科学和信息科学的基本问题的常用工具。