计算平均指标

平均指标按说明现象总体时间状态的不同，分为静态平均指标和动态平均指标两种。静态平均指标，又称静态平均数，是由同一时间条件下总体各单位的标志值计算出来的平均数；动态平均指标，又称动态平均数，是由不同时间条件下总体同种指标数值计算出来的平均数。一般所说的平均指标指的是静态平均指标。

（一）平均指标的含义

平均指标，又称平均数，是用来反映总体各单位某一数量标志标志值在一定时间、地点条件下所达到的一般水平的统计指标。例如，全班学生的平均成绩、全村耕地的平均亩产等，都是平均指标。平均指标将总体各单位标志值之间的差异抽象化了，用一个具体数值说明了总体所有单位标志值的一般水平，它可能不等于总体内任何一个单位的具体水平，但对总体具有代表性。

（二）平均指标的作用

平均指标在认识社会经济现象总体数量特征方面具有十分重要的作用，主要表现在以下几个方面：

1. 反映总体各单位变量值分布的集中趋势

总体各单位的变量值往往是大小不一、存在差异的，但这种差异并不是毫无限制的，它们总是围绕着平均数上小波动，以平均数为中心，因而平均指标反映了标志值变动的集中趋势。例如，人的身高，非常矮的人和非常高的人都较少，而多数人的身高趋近于一般水平（即平均身高）。

2. 比较同类现象在不同时空范围的差异

在不能直接用总量指标比较说明各单位的生产水平、经济效益或工作质量的差异的情况下，可以考虑用平均指标。例如，评价两个同类商业企业营业员的劳动效率，就不能用销售总额这个总量指标进行比较，而用平均指标人均销售额就比较恰当。

3. 分析现象之间的依存关系

在对总体进行分组的基础上，应用平均指标可以分析现象之间的相互依存关系。例如，把若干块耕地的每亩施肥量与平均亩产进行比较，可以发现施肥量和农作物产量之间的依存关系，即在一定范围内，施肥量与农作物产量之间成正相关关系。

根据计算方法的不同，平均指标分为算术平均数、调和平均数、几何平均数、众位和中位数等，它们都可以反映现象的一般水平。算术平均数、调和平均数和几何平均数是根据总体各单位所有标志值来计算的，故统称为数值平均数；而众数和中位数是根据标志值所具有的特殊性质或所处的特殊位置来确定的，故统称为位置平均数。

（一）算术平均数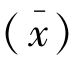

算术平均数就是通常所说的平均数，是指总体各单位的某一数量标志标志值之和（总体标志总量）除以总体单位数（总体单位总量）所计算的结果。其基本计算公式是：

计算算术平均数的方法称为算术平均法。如果社会经济现象总体的标志总量等于各单位标志值的总和，计算平均数，就适合采用算术平均法。

算术平均数也是两个不同性质总量指标的对比结果，因而它和强度相对指标有相似的地方，但实质上它们有很大的区别。平均指标是同一个总体的标志总量与单位总量的对比结果，分子、分母指标之间存在一一对应关系，分子指标中的“标志”就是分母指标中“总体单体”的一个数量标志。例如，计算50名工人的平均工资，作为分子的工资总额就是这50名工人各自工资额的总和，与工人人数之间具有一一对应关系。

强度相对指标不是同一总体的标志总量与单位总量对比计算出来的，分子、分母指标之间没有一一对应关系，分子指标中的“标志”不是分母指标中“总体单体”的标志。例如，人均粮食产量是粮食总产量与人口数对比计算出来的，反映了人口发展对粮食生产能力的依赖程度。但是并非每个人都直接从事粮食生产，粮食产量并不是每个人的有效标志，粮食总产量也不是直接依附所有人口，两个指标之间没有直接的对应关系。

由于所掌握资料的形式不同，算术平均数有两种不同的计算方法，相应的有两种不同的形式：简单算术平均数与加权算术平均数。

1. 简单算术平均数

当已知总体各单位的标志值，且这些标志值未经分组形成变量数列时，宜采用该种形式。其计算过程是：将各单位的标志值相加得到总体标志总量，然后除以总体单位数（即总体单位总量），得到平均数。计算公式为：

式中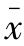，——算术平均数；

x——各单位标志值；

n——总体单位数。

这种计算算术平均数的方法称为简单算术平均法。

例4-9　某教研室有10名教师，年龄分别为23岁、26岁、28岁、34岁、35岁、35岁、43岁、46岁、51岁、53岁。则该教研室教师的平均年龄为：

2. 加数算术平均数

当所依据资料是在统计分组基础上所形成的变量数列资料时，宜采用该种形式。其计算过程是：将各组的变量值（或组中值）与各组的单位数相乘，计算出各组的标志总量，将各组标志总量相加得到总体标志总量，然后除以各组单位数之和（即总体单位总量），得到平均数。计算公式为：

式中，x——各组变量值（或组中值）；

f——各组次数；

n——组数。

这种计算算术平均数的方法称为加权算术平均法。

例4-10　某班50名学生年龄分布如表4-1所示。

表4-1　某班50名学生年龄分布表和平均年龄计算

则该班学生平均年龄为：

例4-11　某学校100名教师工资月工资额分布如表4-2所示。

表4-2　某学校100名教师月工资额分布表和平均月工资额计算

则该学校教师平均月工资额为：

因为从组距式数列已无法看出各个总体单位具体的变量值，所以总体算术平均数已不能够精确计算。按照上述加权算术平均数公式计算，是将组中值作为组内单位的平均水平，得到的一个近似结果。

从以上公式可以看出，决定加权算术平均数结果的因素有两个：各组变量值（或组中值）x和次数f。若各组变量值（或组中值）一定，则次数在计算加权算术平均数过程中具有权衡轻重的作用，即如果某组的次数越大，则计算出的平均数结果同该组变量值（或组中值）的差距越小；而某组的次数越小，则计算出的平均数结果同该组变量值（或组中值）的差距越大，所以称次数为权数。

权数除了用各组次数这种绝对数表示外，还可以用频率这种相对数形式表示。此时，加权算术平均数计算公式为：

式中，——各组频率。

其他符号同上。

比如，例4-10中，学生的平均年龄也可以这样计算：

例4-11中，教师的月平均工资额也可以这样计算：

调和平均数是指总体各单位标志值倒数的算术平均数的倒数，也称为倒数平均数。根据所掌握资料的形式不同，分为简单调和平均数和加权调和平均数两种。

1. 简单调和平均数

当已知总体各单位的标志值，且这些标志值未经分组形成变量数列时，采用该种形式。其计算公式为：

式中，——调和平均数；

x——各单位标志值；

n——总体单位数。

2. 加数调和平均数

当所依据资料是在统计分组基础上所形成的变量数列资料时，宜采用该种形式。其计算公式为：

式中，x——各组变量值（或组中值）；

f——各组次数；

n——组数。

实际上，在统计分析中，往往并不按调和平均数的上述定义直接进行计算，因为按此定义计算出的结果没有实际意义，并不代表各单位标志值的一般水平。统计工作中运用调和平均数，主要是运用它的以上两个运算公式，并且将它们作为加权算术平均数计算公式的变形公式使用。以下是变形过程：

设xi，fi，mi(i=1，2，…，n）是变量数列各组的变量值、次数、标志总量，则有xifi=mi及，则

不难发现，此式与加权调和平均数计算公式在形式上完全相同，而实际工作中就是按照该式中符号的含义来使用调和平均数的。当各组标志总量相等且等于1时，要使用简单调和平均数公式计算平均数；当各组标志总量不完全相等时，要使用加权调和平均数公式计算平均数。

例4-12　某天某种蔬菜，早市每斤①0.25元，午市每斤0.2元，晚市每斤0.1元，现在从早市、午市、晚市各买1元的，则购回蔬菜平均价格为：

例4-13　若上例中，其他条件不变，现在从早市花3元购买，午市上花2元、晚市上花1元，则购回蔬菜平均价格为：

例4-14　某企业有甲、乙、丙三个车间，生产同一种产品，某月各车间产品单位成本、产量和总成本资料如表4-3所示。

表4-3　某企业平均产品单位成本计算

若掌握的是各车间产品单位成本和产量资料，则该企业平均产品单位成本为：

若掌握的是各车间产品单位成本和总成本资料，则该企业平均产品单位成本为：

不难发现，加权算术平均数公式和加权调和平均数公式都可以计算一般所说的平均数，只不过依据的资料不同而已。若已知各组变量值（或组中值）及次数资料，采用加权算术平均数公式计算平均数；若已知各组变量值（或组中值）及标志总量资料，采用加权调和平均数公式计算平均数。

（三）几何平均数

几何平均数是对各变量值的连乘积开项数次方根。求几何平均数的方法叫做几何平均法。如果总水平、总成果等于所有阶段、所有环节水平、成果的连乘积而非总和时，求各阶段、各环节的一般水平、一般成果，要使用几何平均法计算几何平均数，而不能使用算术平均法计算算术平均数。根据所掌握资料的形式不同，其分为简单几何平均数和加权几何平均数两种形式。

1. 简单几何平均数

当已知总体各单位的标志值，且这些标志值未经分组形成变量数列时，采用该种形式。其计算公式为：

式中，——几何平均数；

x——各变量值；

n——变量值项数。

这种计算几何平均数的方法叫做简单几何平均法。

例4-15　某工厂某产品的生产需要依次经过三个车间的三道工序，前道工序生产的合格产品方能进入下一道工序继续进行加工。已知三个车间的产品合格率分别为87%、91%和89%，求三个车间平均的产品合格率。

由于全厂总的产品合格率等于三个车间产品合格率的连乘积而非总和，所以要采用几何平均法而非算术平均法计算各车间平均的产品合格率，即三个车间平均的产品合格率为：

2. 加权几何平均数

当所依据资料是在统计分组基础上所形成的变量数列资料时，采用该种形式。其计算公式为：

式中，x——各组变量值；

f——各组次数；

n——组数。

这种计算几何平均数的方法叫做加权几何平均法。

例4-16　某大型精密仪器的生产需要依次经过10道工序，前道工序生产的合格产品方能进入下一道工序继续进行加工，已知各工序的产品合格率如表4-4所示。

表4-4　某仪器各生产工序产品合格率

则该仪器各道工序平均的产品合格率为：

（四）众数（M0）

众数是指总体中出现次数最多的标志值。它与算术平均数的作用一样，也可以反映总体各单位标志值的一般水平，只是精确度较差。它是一种位置平均数，不受数列中极端变量值的影响，这是它与算术平均数的主要区别。值得注意的是，并非任何总体中都存在着众数，只有当总体各单位的标志值具有明显的集中趋势时，才存在众数，如果它们趋于均匀分布，就不存在众数。

要直接确定众数，只能依据分组资料。如果是未分组资料，首先应进行统计分组。

1. 单项式数列的众数

确定单项式数列的众数是非常容易的，次数最多的那一组的变量值就是众数。

例4-17　某班50名学生年龄分布如表4-5所示。

表4-5　某班50名学生年龄分布

从表4-5可以直接看出，18岁学生人数最多，为28人，因此18岁就是众数。

2. 组距式数列的众数

计算组距式数列的众数，相对来说要复杂一些，首先应将次数最多的那一组作为众数组，然后运用众数的下限公式或上限公式进行近似计算。

式中，M0——众数；

L——众数组下限；

U——众数组上限；

Δ1——众数组次数与前一组次数之差；

Δ2——众数组次数与后一组次数之差；

d——众数组组距。

例4-18　某班40名学生某次《英语》课考试之后成绩分布如表4-6所示。

表4-6　某班40名学生《英语》课成绩分布

从表4-6可以直接看出，70～80组人数最多，为18人，因此该组最有可能是众数组。

运用下限公式计算：

运用上限公式计算：

从计算结果可以看出，下限公式和上限公式的计算结果是一致的，实际统计工作中，用哪一个公式都可以。

（五）中位数（M）

中位数是指总体各单位的标志值按大小顺序排列后，位于中间位置的标志值。也就是说，中位数是位于标志值数列中心位置的那个标志值，在它的前后各有50%的标志值。可见中位数是以处于中心位置的标志值代表总体各单位标志值的一般水平的，所以它与众数一样，代表性也较差。中位数也是一种位置平均数。

1. 未分组资料的中位数

确定未分组资料的中位数相对来说较为容易，首先将所有标志值按大小顺序排列，然后确定数列的中点位置。不论数列项数是奇数项还是偶数项，中点位置均在第项上。如果数列是奇数项，则中点位置上的标志值即为中位数；如果数列是偶数项，则中点位置前后两个标志值的算术平均数即为中位数。

例4-19　有一学习小组，由7名学生组成，其年龄分别为：21岁、21岁、22岁、22岁、22岁、23岁、24岁。则在该学习小组学生的年龄中，中点位置为：，因为数列项数是奇数项，所以中位数就是中点位置（第4个位置）上的年龄22岁。

例4-20　另有一学习小组，由8名学生组成，其年龄分别为：21岁、21岁、21岁、22岁、22岁、22岁、23岁、24岁。则在该学习小组学生的年龄中，中点位置为：，因为数列项数是偶数项，所以中位数是第4个位置上年龄22岁与第5个位置上年龄22岁的算术平均数，结果为22岁。

2. 已分组资料的中位数

已分组资料有单项式数列和组距式数列两种，它们的中位数确定方法各异。

1）单项式数列的中位数

确定单项式数列中位数时，首先用公式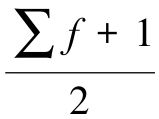确定中点位置，然后计算各组累计次数并确定中位数组（即中位数所在组）及中位数。

例4-21　确定表4-5中某班50名学生年龄的中位数。

中点位置为：

由于中位数处于第25.5位上，由向上累计次数可以看出，前两组累计人数为6人，而前三组累计人数为34人，所以中位数肯定在第三组，也就是说第三组为中位数组，则第三组的变量值就是中位数，即中位数为18岁。

2）组距式数列的中位数

组距式数列与单项式数列中位数组的确定方法完全相同。不同的是，确定出组距式数列中位数组以后，需要运用中位数的下限公式或上限公式进行近似计算。

式中，Me——中位数；

L——中位数组下限；

U——中位数组上限；

fm——中位数组的次数；

sm-1——中位数组以前各组次数总和（即前一组向上累计次数）；

sm+1——中位数组以后各组次数总和（即后一组向下累计次数）；

∑f——为总次数；

d——中位数组的组距。

例4-22　确定表4-6中某班40名学生《英语》课成绩的中位数。

中点位置为：

由于中位数处于第20.5位上，由向上累计次数可以看出，前两组累计人数为8人，而前三组累计人数为26人，所以中位数肯定在第三组，也就是说第三组为中位数组。