位置平均指标

第二节　位置集中趋势测量:位置平均指标

由于组平均数难以反映整个平均数，有时平均数在现实生活中并非存在，比如某单位5个人，老板10000元，4个员工月薪3000元，平均月薪4400元，但是实际上没有一个月薪是4400元。因此人们往往使用位置平均数。经常使用的位置平均数有中位数、众数和四分位数等，这些位置平均数并不要求数据呈等距分组。

一、中位数

中位数(Median)是数据按照大小排列出来以后，中间位置的数值。这样有一半数据比中位数大，同时有一半数据比中位数小。中位数比算术平均值稳定，而且受极值的影响小，因而在经济统计中应用较多。

不分组情况下中位数的计算，事先是寻找中位数的位置，然后计算中位数的数值。将样本数据(假设有N个数)按升序或降序排列，如果N为奇数，则数列中间的数为中位数；如果N为偶数，则中位数为其中两个数的均值。

若以表2.4某班50名学生的社会学考试成绩为例，数据排序以后，中位数位置为(50+1)/2，即25、26数据的平均，为74.5分。

分组情况下的中位数(Group Median)，是先找到中位数所在的组，然后用线性内插的方法进行计算。

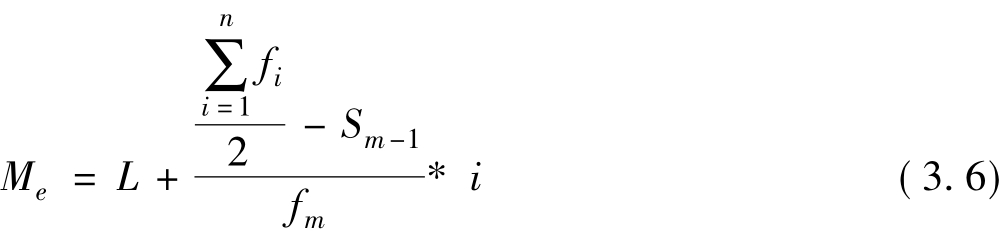
式中L是中位数所在组的下限，f_m是中位数所在组的频数，i是中位数所在组的组距，∑f是各组次数之和——总次数，S_m－1是到中位数所在前一组的累积次数之和。中位数的具体求法是，先寻找中位数所在组位置，确定中位数所在组频数f_m、组距i和所在组下限L，计算中位数前一组各组次数累计和S_m－1，然后，代入公式计算中位数。中位数的几何意义是将图形分割成面积相同的两个部分。

［例3.4］若取例3.1数据，通过向上累计可见，∑f/2=150在第三组，10000～15000之间，接着，可见中位数所在组的下限L=10000，中位数所在组的频数f_m为105，中位数所在组的组距i是5000，到中位数所在前一组的累积次数之和S_m－1是72，代入公式，可计算得:

即这300户农民家庭年纯收入中位数为13714元，有150户比该数低，同时有150户比该数高。

表3.2　　　　　　　　　　300农户经济收入的向上、向下累计表

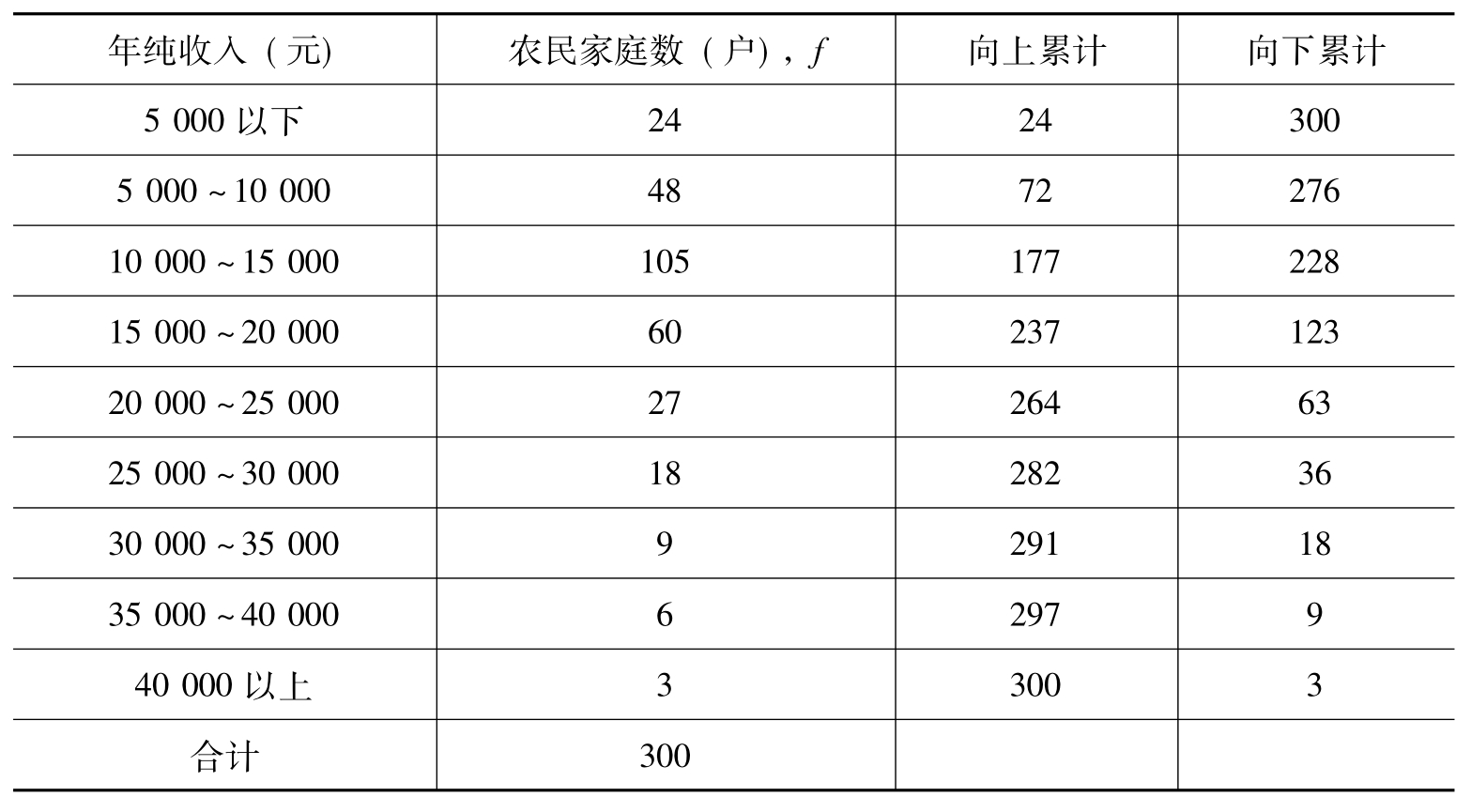
应该说明的是，以上使用的是上限公式，类似若使用下限公式结果完全一致；上文使用的是频数，如果使用频率结果完全一致。

二、众数

数据中最经常出现的那个数，即频数(次数)最大的那个数称为众数(Mode)。统计学中常利用众数来说明社会现象的一般水平，如成人衣服、鞋袜等都使用众数来组织生产。与中位数类似，众数不受极值影响。但有时会出现2个甚至多个众数，有时又没有众数。所以，众数的使用受到严格限制。在不分组的情况下，出现频数最多的数就是众数。若以表2.4某班30名学生的年龄为例，18岁出现了14人，频(人)数最高，为众数。

在资料分组的情况下，众数的计算思想是寻找众数所在组，然后根据相邻组的频数进行选择和修正，具体公式如下:

Mo=L+(d₁*i)/(d₁+d₂)　　　　　　　　　　　　　　(3.7)

式中L是众数所在组的下限，i是众数所在组的组距，d₁是众数所在组次数与上一组次数的差异，d₂是众数所在组次数与下一组次数的差异。

同样，由例3.2数据，先确定众数所在组位置，第三组的下界L=10000；计算众数与其前、后组次数之差异d₁=105－48、d₂=105－60，及组距i= 5000；然后，代入公式计算众数

Mo=10000+(57*5000)/(57+45)=12794(元)

类似的有，计算众数的下限公式。

三、中位数、众数和算术平均数之间的关系

算术平均数适用于定距尺度、定量尺度的资料，其利用全部数据计算而得，具有高度的数字灵敏性和代表性，在统计分析和统计推断中具有重要的地位。中位数虽不受极端标志数值的影响，可扩展应用于定序尺度；但数学敏感性差，损失信息较多，不便于作简单的代数运算，在高级统计分析中使用受限。众数概念简捷明了，通俗易懂，不受极端变量值的影响，可以在定类计量尺度中运用；但稳定性差，不具惟一性，无法进行代数运算。同样，在高级统计分析中受到严重的限制。综合而言，算术平均数和中位数使用比较频繁。

算术平均数、中位数和众数三者之间存在着一定的数量关系，这种关系决定于总体中次数分布的实际状态。在单峰分布条件下，当数据呈正态分布时，总体内次数分布两边呈完全对称的钟形曲线，这时算术平均数处于钟形曲线的对称点上，对称点又是曲线的中心点和最高点，因此，算术平均数、中位数和众数处于同一位置上，即: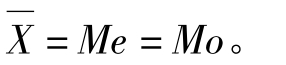

在数据呈偏态分布时，算术平均数、中位数和众数就存在差别，这种差别与非对称的程度大小有关。非对称的程度愈大。它们之间的差距愈大；反之，非对称的程度愈小，其差距愈小。次数分布中如果出现极大值，必然将算术平均数拉向极大值方向，中位数也相应增大，众数依然保持不变，由此形成的次数分市曲线就会呈现有偏斜状态。这时，算术平均数、中位数和众数之间的关系就表现为: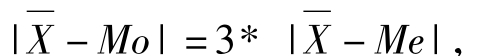如图3.1所示。

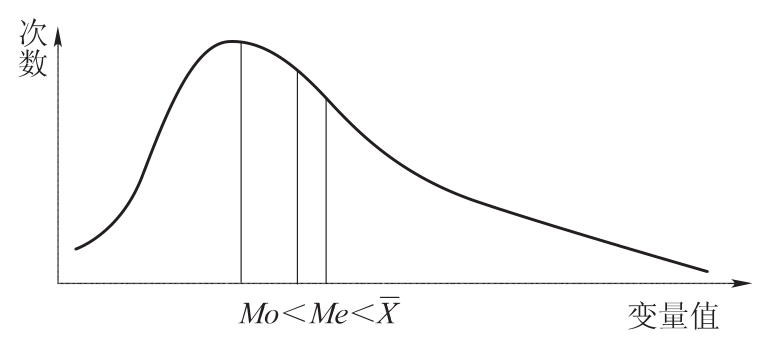
图3.1　右偏分布下的Me、Mo和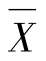的关系

当数据呈现左偏态分布时，说明数据存在极端的小值，必然将算术平均数拉向极小值方向，中位数也相应减小，而众数依然保持不变，于是就有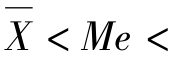Mo，如图3.2所示。

由此可见，中位数一定位于算术平均数和众数之间。统计学家卡尔·皮尔逊的研究结果表明，在钟形分布只存在轻度偏斜的情况下，不论是右偏还是左偏，算术平均数、中位数和众数三者的关系是:算术平均数与众数的距离约等于算术平均数与中位数距离的三倍，即: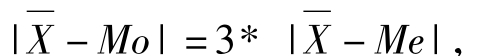但这仅是大致的经验公式，非资料不全万不得已不要使用该公式。

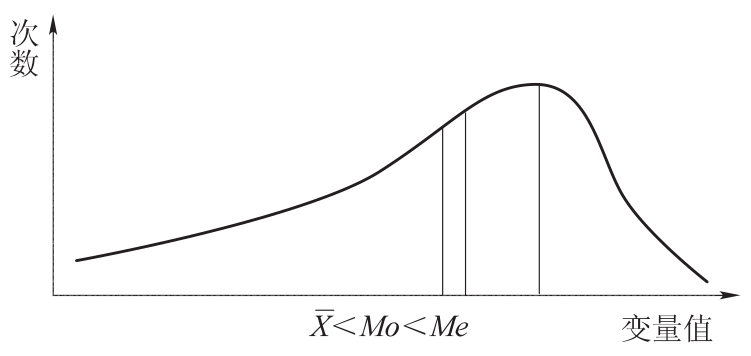
图3.2　左偏分布下的Me、Mo和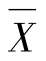的关系

四、四分位数

最低数与中位数之间的中位数是25分位数或第一个四分位数，而中位数与最高数之间的中位数是75分位数也称第三个四分位数。类似中心趋向的度量还有十分位数和百分位数。和中位数一样，四分位数的计算，首先应该确定四分位数的具体位置((n+1)/4，3*(n+1)/4)，而后确定其值。而分组数据和未分组数据计算四分位数都有所差异。

如果有10个家庭年经济收入分别为1.5、2.1、3.3、4.5、5.2、6.4、7.8、8.2、9.8、12.0万人民币，则经过排序以后，第一、三个四分位数(Q₁、Q₃)分别在2.75位和8.25位，于是:

Q₁=2.1+3*(3.3－2.1)/4=3.0
Q₃=8.2+1*(9.8－8.2)/4=8.6

再以表2.4某班50名学生的社会学考试成绩为例，Q₁、Q₃分别在51/4= 12.75位和153/4=38.25位，排序以后，发现相应第一、三个四分位数分别为66.75和84.0。

组距数列求四分位，前三步与品质(定序)数列、单项数列的计算方法完全一致。即第一步求四分位数的位置；第二步计算累计次数；第三步确定四分位数所在组。只是这时因四分位数所在组是一个组距，故还需运用插值公式计算四分位数的近似值。

下面是四分位数Q₁的下限公式:

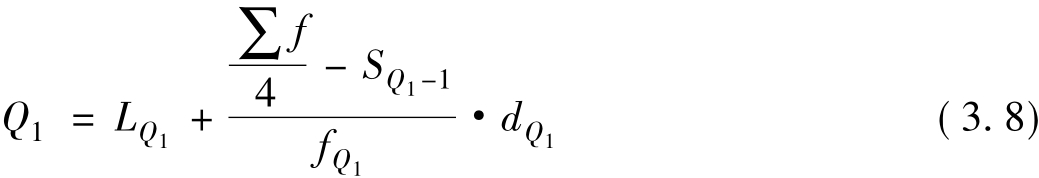
式中　L_Q1——四分位数所在组的下限数值；

　S_Q1－l——到四分位数所在组，组下限以下各组的累计次数；

　f_Q1——四分位数所在组的次数；

　d_Q1——四分位数所在组的组距数值。

十分位数、四分位数和百分位数的计算类似中位数的计算。在分组数据中，应该首先决定所要的位置量度落在哪一个间距中。若取例3.2数据，可以定出第N/4个或第75个个案而得到第1个四分位数。从累积频数列中看出，第1个四分位数一定在10000元到15000元的间距内某个地方。由于这个间距内有105个个案，所要跳过这段距离的(75－72)/105。因此第1个四分位数Q₁的值应该是:

Q₁=10000+(75－72)*5000/105=10000+143=10143元

Q₃=15000+(225－177)*5000/60=15000+4000=19000元

其他位置量度可以用类似的方式来计算。根据定义，中位数相当于第2个四分位数、第5个十分位数和第50个百分位数。

和中位数相似，第1个四分位数的值表示，有1/4的个案数值小于该值；同样，第三个四分位数代表着3/4的个案小于它的那个数值。如果愿意，可以把分布分成10个十分位数，用1/10、2/10或9/10等小于它的数值的个案来定。同学也许更熟悉百分位数，若把分布分成100个等份。有某学生在考试中落入第91个百分位数里，就可以知道91%的学生的分数成绩比他低。十分位数、四分位数和百分位数在社会学研究中使用场合有限，但比较重要，应该熟悉它们的基本意义。

应该注意的是，平均指标使用前提。比如平均年龄的计算就有所不同，由于人的年龄是按周岁申报、计算的，具体取值不是常态的“四舍五入”方法，而是“截尾”方法。某人年龄16岁，实际代表的是16.0－16.9岁，而货币16元代表的是15.5元－16.4元。因此，最后计算的平均年龄应该加上0.5岁。比如有三人实际年龄分别为18.9岁、21.6岁、20.5岁，他们申报年龄分别为18岁、21岁、20岁，原方法计算平均年龄为19.7岁，而新方法去加上0.5岁以后为20.2岁，显然，新方法比较接近实际平均年龄(20.3岁)。其他年龄的中位数和众数计算类似。