假设检验的基本思想

（一）问题的提出

在介绍假设检验的统计思想前，先看几个例子。

例8.1.1　设某种清漆的9个样品，其干燥时间（以小时计）分别为：

根据以往经验，干燥时间的总体服从正态分布N（6.0，0.36），现根据样本检验平均干燥时间是否与过去有显著差异？

例8.1.2　一种摄影药品被其制造商声称其贮藏寿命是均值180天、标准差不多于10天的正态分布。某位使用者担心标准差可能超过10天。他随机选取12个样品并测试，得到样本标准差为14天。根据样本有充分证据证明标准差大于10天吗？

例8.1.3　通常认为男女的脉搏率是没有显著差异的。现在随机地抽取16位男子和13位女子，测得他们的脉搏率如下：

设男女脉搏率都服从正态分布，问能否根据这些数据接受假设：男女脉搏率的均值相同？

例8.1.4　孟德尔遗传理论断言，当两个品种的豌豆杂交时，圆的和黄的、起皱的和黄的、圆的和绿的、起皱的和绿的豆的频数将以比例9：3：3：1发生。在检验这个理论时，孟德尔分别得到频数315，108，101，32，这些数据提供充分证据拒绝该理论吗？

例8.1.1，例8.1.2和例8.1.3都是在已知总体是正态分布的前提下，要求对有关总体的均值或标准差的假设给出检验，是属于参数检验，我们将在第2、3节中讨论；例8.1.4实际上可以看成对总体的分布提出假设，这就是第5节中要讨论的分布拟合检验问题。

统计假设简称为假设，通常用字母H表示一般我们同时提出两个完全相反的假设，习惯上把其中的一个称为原假设或零假设，用H0表示，把另一个假设称为对立假设或备择假设，用H1表示。如例8.1.1中以μ代表清漆的平均干燥时间，则原假设和备择假设可以分别写成。原假设和备择假设的划分并不是绝对的，一般地，在有关参数的假设检验中，备择假设是我们根据样本资料想得到支持的假设。显然，对于任何一个假设检验问题，结论只能是H0和H1两者中必居其一。

关于总体参数θ的假设有三种情况：为已知的常数。以上三种情况中，有关第（1），（2）种假设的检验称为单边检验，第（3）种假设的检验称为双边检验，其中第（1）种称为左边检验，第（2）种称为右边检验。

（二）检验统计量和拒绝域

如何对提出的各种不同假设进行检验呢？下面我们通过对例8.1.1来说明假设检验的基本思想。

在例8.1.1中，设某种清漆的干燥时间为X，由已知，为已知，现在要对参数μ提出假设

根据第七章参数估计的理论，样本均值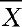是参数μ的无偏估计。的取值大小反映了μ的取值大小。当原假设H0成立时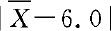，取值应偏小，反之，当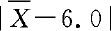取值偏大时，我们认为原假设H0成立的可能性很小。因此，我们可以根据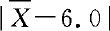的取值大小来制定检验规则。也就是说，按照规则：

对原假设H0作出判断，其中临界值C是一个待定的常数。不同的C值表示不同的检验。如何确定C，我们将在后面作介绍。

一般地，在假设检验问题中，若寻找到某个统计量，其取值大小和原假设H0是否成立有密切联系时，我们将之称为该假设检验问题的检验统计量，而对应于拒绝原假设H0时，样本值的范围称为拒绝域，记为W，相应的W的补集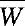称为接受域。根据上面的分析，例8.1.1中，我们可取检验统计量为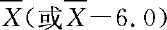，而拒绝域为

因此，对于一个假设检验问题，给出一个检验规则，相当于在样本空间中划分出一个子集，将之作为检验的拒绝域。反之，给出一个拒绝域也就给出了一个检验规则。如何选取检验的拒绝域成为假设检验的一个关键问题。这不仅需要对实际问题的背景有足够的了解和丰富的统计思想，还需要在理论上有评价检验好坏的标准。为此，我们需要介绍假设检验问题中可能犯的两类错误。

（三）两类错误

根据样本推断总体，由于抽样的随机性，所作的结论不能保证绝对不犯错误，而只能以较大的概率保证其可靠性。在假设检验推断中可能出现下列四种情形：

（1）拒绝了一个错误的原假设；

（2）接受了一个真实的原假设；

（3）拒绝了一个真实的原假设；

（4）接受了一个错误的原假设。

（1）和（2）两种情形是正确的决定，而（3）和（4）两种情形都是错误的决定，其中情形（3）所犯的错误，我们称为犯第Ⅰ类错误，也称为弃真错误，情形（4）所犯的错误，我们称为犯第Ⅱ类错误，也称为取伪错误。通常，用α表示犯第Ⅰ类错误的概率，用β表示犯第II类错误的概率。具体地，有

现在，我们来计算上述例8.1.1中的检验规则所犯两类错误的概率。

犯第Ⅰ类错误的概率

由于当原假设H0为真时，即，则有

犯第Ⅱ类错误的概率

由（8.1.1）知，犯第Ⅰ类错误的概率α（C）关于临界值C是单调减函数，而由（8.1.2）知，犯第Ⅱ类错误的概率β（C）关于临界值C是单调增函数。所以在样本容量n固定时，犯这两类错误的概率是相互制约的。若要同时使得犯两类错误的概率都很小，就必须有足够大的样本容量。这样随之而来的是我们在人力、物力和时间上付出的代价就增加了。

鉴于上述情况，奈曼和皮尔逊提出：首先控制犯第Ⅰ类错误的概率，即选定一个常数，要求检验犯第Ⅰ类错误的概率不超过α，然后在满足这个约束条件的检验中，再寻找检验，使得犯第II类错误的概率尽可能小。这就是假设检验理论中的奈曼—皮尔逊原则，其中的常数α称为显著水平。α的大小取决于我们对所讨论问题的实际背景的了解。在通常的应用中，常取α为0.01，0.05 ，0.10等。

在例8.1.1中，若取显著水平α＝0.05，即要求犯第Ⅰ类错误的概率不超过0.05，则由（8.1.1）

根据奈曼—皮尔逊原则，为使得犯第II类错误的概率尽可能小，我们应选取C＝O.392，因此拒绝域为

根据样本实际观测，计算得，即样本落入拒绝域，因此我们有95％的把握拒绝原假设H0，即认为油漆干燥时间与以往有显著差异。

（四）P_值与统计显著性

当原假设H0为真时，检验统计量取比观察到的结果更为极端的数值的概率，称为P_值。在实际运用中，通过计算P_值来衡量拒绝H0的理由是否充分。P_值较小说明观察到的结果在一次试验中发生的可能性较小，P_值越小，拒绝H0的理由越充分；P_值较大说明观察到的结果在一次试验中发生的可能性较大，所以没有足够的理由拒绝H0。

在例8.1.1中，当H0为真时，检验统计量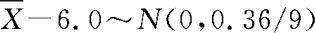，根据样本实测得，即有，则可计算得

P_值为0.046，表示1000次重复试验中，只有约46次允许。因此，当H0为真时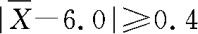，可以看成小概率事件。一般地，我们认为小概率事件在某一次具体的观察中是几乎不发生的，但目前的样本资料表明，该事件确实已经发生，这意味着H0为真的假设是不合理的，所以我们应该作出拒绝原假设H0的判断。

当假设检验的显著性的水平为α，若P_值小于等于α，则拒绝原假设，此时我们称检验结果在水平α下是统计显著的。

可以说P_值提供了比显著水平α更多的信息，根据P_值，我们可以判定在任何给定显著性水平下检验结果是否显著。如P_＝0.03，则说明在α＝0.05水平下是显著的，但在α＝0.01水平下却不显著。

（五）处理假设检验问题的基本步骤

通过对例8.1.1的介绍，一般的假设检验问题我们可按下列步骤进行：

（1）根据实际问题提出原假设和备择假设；

（2）提出检验统计量和拒绝域的形式；

（3）根据奈曼—皮尔逊原则和给定的显著水平α，求出拒绝域W中的临界值；

（4）根据实际样本观测值作出判断。

其中步骤（3），（4）也可如下进行：

（3′）计算检验统计量的观测值和P_值；

（4′）根据给定的显著水平α，作出判断。

一般的统计分析软件处理假设检验问题都是通过计算P_值而不是给出拒绝域W来作出判断的。在下面的章节中，我们将结合两种思想来介绍假设检验问题。