随机变量的相互独立性

独立性的概念在概率论中是非常重要也是最基本的概念．它在概率论和数理统计应用中占有很重要的地位．

定义3．3．1 设X和Y为两个随机变量，并设F（x，y），FX（x），FY（y）分别是二维随机变量（X，Y）的分布函数及边缘分布函数．若对于任意的实数x，y，有

P｛X≤x，Y≤y｝＝P｛X≤x｝·P｛Y≤y｝，

即

F（x，y）＝FX（x）·FY（y）， 　（3－15）

则称随机变量X与Y相互独立．

设（X，Y）是二维离散型随机变量，则X，Y相互独立的充要条件是

P｛X＝xi，Y＝yi｝＝P｛X＝xi｝·P｛Y＝yi｝， 　（3－16）

即 　pij＝pi··p·j，i，j＝1，2，…．

这里pij，pi·，p·j分别是（X，Y），X，Y的分布侓．

例3．3．1 设二维随机变量（X，Y）的联合分布律为

求：①求a，b应满足的条件；

②若X与Y相互独立．求a，b的值．

解 ①根据非负性和规范性可知

②因为X与Y相互独立．则知 pij＝pi··p·j，

设（X，Y）是二维连续型随机变量，则X，Y相互独立的充要条件是联合概率密度等于边缘概率密度的乘积．即

f（x，y）＝f X（x）·f Y（y） 　（3－17）

其中f（x，y），f X（x），f Y（y）分别是（X，Y）的联合概率密度及边缘概率密度．

证明 “⇐”若f（x，y）＝f X（x）·f Y（y），则

即 X．Y相互独立．

“⇒”由独立的定义

F（x，y）＝FX（x）·FY（y）

由联合密度函数的定义知：f X（x）·f Y（y）是（X，Y）的联合密度函数，即f（x，y）＝f X（x）·f Y（y）．

例3．3．2 设（X，Y）的分布函数为

求：①求常数A，B，C；

②判断X与Y是否相互独立；

③f（x，y），f X（x），f Y（y）．

解 ①由于1＝F（＋∞，＋∞）＝A·（B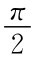－）·（C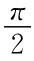＋），得A≠0．

又 0＝F（－∞，y）＝

同理 0＝F（x，－∞）＝得

故

②由于 FX（x）＝F（x，＋∞）＝，FY（x）＝F（＋∞，y）＝＋arctan），则F（x，y）＝FX（x）·FY（y），所以X与Y相互独立．

③由于f X（x）＝F′X（x）＝

因为X与Y相互独立，则

例3．3．3 设X与Y是两个相互独立的随机变量．X在（0，0．2）上服从均匀分布，Y的概率密度为

求P｛Y≤X｝．

X与Y相互独立，故（X，Y）的概率密度为

其中D＝｛（x，y）0＜x＜0．2，y＞0｝，G＝｛（x，y）y≤x｝．

以上所述关于二维随机变量的联合分布函数、联合概率密度、独立性等概念，容易推广到n维随机变量中去．

注：①若X1，X2，…，Xn两两独立不能得到X1，X2，…，Xn相互独立；

②随机变量的独立性不具有传递性；

③对于（X，Y）而言，由（X，Y）的分布可以确定关于X与Y的边缘分布，反之一般不成立．只有当X与Y独立时，由边缘分布能确定联合分布；

④随机变量的独立性是随机事件独立性的扩充．我们也常利用问题的实际意义去判断两个随机变量的独立性．