【摘要】：，n，q＝1－p，则由此可知：正态分布的概率密度中的两个参数μ和σ分别是该分布的数学期望和均方差，因而正态分布完全可由它的数学期望和方差所决定．再者，若Xi～N（μi，），i＝1， 2，…，n，且它们相互独立，则它们的线性组合c1X1＋c2X2＋…＋cnXn（c1，c2，…，cn是不完全为零的常数）仍然服从正态分布，由数学期望和方差的性质知道：
下面计算一些重要分布的方差，为书写方便，一律假定相应的随机变量为X．
1．两点分布
若随机变量X～B（1，p），其分布律为P｛X＝x｝＝px（1－p）1－x，x＝0，1，则
E（X2）＝p，D（X）＝p（1－p）．
2．二项分布
若随机变量X～B（n，p），其分布律为P（X＝k）＝Cknpkqn－k，k＝0，1，2，…，n，q＝1－p，则
3．泊松分布
若随机变量X～P（λ），其分布律为P（X＝k）＝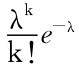
，k＝0，1，2，…，λ＞0），则
4．均匀分布
若随机变量X～U［a，b］，其分布密度函数为f（x）＝
则
5．指数分布
若随机变量X～E（λ），其分布密度函数为
6．正态分布
若随机变量X～N（μ，σ2），其分布密度函数为
由此可知：正态分布的概率密度中的两个参数μ和σ分别是该分布的数学期望和均方差，因而正态分布完全可由它的数学期望和方差所决定．再者，若Xi～N（μi，
），i＝1， 2，…，n，且它们相互独立，则它们的线性组合c1X1＋c2X2＋…＋cnXn（c1，c2，…，cn是不完全为零的常数）仍然服从正态分布，由数学期望和方差的性质知道：
这是一个重要的结果，在前面第3章已有此结论．
为了方便使用，现将上面得到的重要分布的数学期望与方差汇集于下表4－4．
表4－4
例4．2．1 设随机变量X的数学期望E（X）＝μ，方差D（X）＝σ2≠0，记X＊＝
则有
X＊称为X的标准化变量．
例4．2．2 设X1，X2分别表示甲、乙手表的日走时误差，则其概率密度分别为
试比较出哪类手表走得更好．
解 
因此D（X1）＜D（X2），即X1的偏离程度小，甲手表走得较好．
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
