商业银行安全可靠性分析

2　银行系统可靠度Copula理论模型

金融风险是指包括金融机构在内的各种经济实体，在从事金融活动和投资经营活动过程中，因各种金融因素(如利率期限结构、货币汇率、股指价格、商品价格、信用和流动因素等)未来变化的不确定性而遭受损失的可能性。不确定性是金融风险产生的根源，不确定性越大，风险越大。根据金融风险的性质和来源不同，金融风险可分为五类:市场风险、信用风险、流动性风险、操作风险、法律风险。

由于金融风险的来源多而复杂，某一种因素可能同时引发几种金融风险。当公司资产的市场价值发生突然变化时，会由市场风险影响公司的信用级别而引发信用风险;而当公司的信用级别发生不期望的变化产生信用风险时，必将会改变公司资产的市场价值而导致市场风险，从而形成市场风险和信用风险难以分解的循环过程。在商业交易中，一个操作上的问题(如交易不能结算)就会同时引起市场风险和信用风险。据ISDA对美国金融业的统计结果，在金融业面临的风险中，信用风险约占总风险的45%、市场风险约占总风险的35%、操作风险约占总风险的20%。要指出的是，破产是在企业资不抵债或不能清偿到期债务时，作出破产宣告，并依法对其财产进行清理、分配的行为。上述五种风险的任何一种风险发展到极端时都可能导致企业破产，所以本书拟对破产风险的建模和计算做一定研究。

机械系统的复杂性导致零件之间、零件各失效模式之间均存在着特定的相关性，外部条件的不同，其相关结构、相关强弱程度不尽相同。由于既不能用不考虑相关性的独立性假设理论，也不能用完全线性相关的最薄弱环节理论来计算系统可靠度，相关性可靠度的计算一直就是结构、机械系统可靠性理论研究的重点和难点(芮延年和傅戈雁，2007)。Ditlevsen(1979)最早考虑了结构系统相关性，基于相关系数给出可靠度的窄界，若零件的个数或零件失效模式数n较大，计算变得非常繁琐，难以实现。Jose和David(2005)提出随机模拟是一种解决方法，但Paradlwrter和Pellissetti(2005)指出Monte Carlo模拟方法的前提是结合有限元方法，对算法程序要求较高，同时由于抽样方法的不同，可能导致偏差较大。国内学者的可靠度计算方法多建立于相关系数ρ之上，但ρ对相关性的刻画仅仅是针对变量之间的一阶整体线性关系，并不能全面反映零件失效之间的实际互动关系(如二阶、高阶、多变量线性、同调性等)。综观国内外文献，相关性可靠性理论至今仍未取得突破，最近的进展是用Copula来拟合各构件失效模式之间的相关关系。

通过上述分析，可以发现构件的失效概率相当于金融机构的破产概率，结构系统的失效概率相当于金融系统的破产概率，本书拟将工程系统安全性研究中的可靠度理论引入金融系统的安全性研究中，同时结合Copula技术来对金融系统的相关性可靠度进行建模和实证，这是一项用另一种视角、另一种方法来研究金融系统破产风险的工作。

2. 1　Copula方法基本原理

不同随机变量之间的联系通常不是独立的，它们相互影响，相互作用。很显然，合理的度量这种相关性对于研究由这些随机变量所形成的函数的性质非常重要，仅用线性相关性已经不足以完全描述随机变量之间的联系，而Copula函数在相关性度量方面则表现出优越的性质。Copula是在20世纪70年代中期研究多变量分布过程中发展起来的一个概念。它描述了多元随机变量之间的相关性结构，使得多元随机变量的联合分布函数可以由随机变量的边缘分布和Copula函数来确定。由于Copula能够全面描述多元随机变量的相关性结构，为线性相关所不能描述的问题提供了研究途径。

Copula一词最早由Sklar于1959年提出，意思是交换、连接。假设随机向量X=(X1，…，Xn)T，其联合分布函数为F(x1，…，xn)= P{X1≤x1，…，Xn≤xn}，分量Xi的边缘分布为Fi(x)= P{Xi≤x}。

2.1.1　Copula函数的定义

一个d维的Copula函数C是一个多元联合分布函数，它具有在［0，1］上的统一均匀分布，且有下面的性质:

(1) C:［0，1］d→［0，1］;

(2) C是有界递增的;

(3) C(u1，…，uk－1，0，uk+1，…，ud)= 0; C(1，…，1，uk，1，…，1)= uk。

很显然，从上面的定义可以看出:如果F1，…，Fd是一维分布函数，当Ui= Fi(Xi) i= 1，…，d时，C(F1(x1)，…，Fd(xd))是具有边缘分布为F1，…，Fd的多元联合分布函数。

2.1.2　Skalr’s定理

如果F是一个具有连续边缘分布函数F1，…，Fd的d维联合分布函数，那么它具有下面唯一的Copula表达式:

从Sklar’s定理可知，对于连续的多元联合分布函数，多元相关结构可以用Copula函数来表示，而边缘分布可以采用适当的函数来描述。金融市场风险分析应用中，边缘分布Fi，i= 1，…，n代表单支股票的风险，而相关结构则代表资产间、市场间的风险。

由上面的形式可得以下推论。

设F是具有连续边缘分布函数F1，…，Fd的d维联合分布函数，且满足式(2.1)的Copula函数C，那么，对于任何［0，1］d中的u=(u1，…，ud)有

式中，Fi－1是Fi的广义逆。这里ui∈［0，1］，ui= Fi－1(x)，i= 1，…，n。可见相关结构C就是边缘分布都服从［0，1］上均匀分布的n维随机变量的联合分布函数。

因此，多元分布函数F的密度函数可以写为

式中，c(·，…，·)和fi(·)分别是Copula连接函数和边缘分布函数的密度函数。由此可见，Copula函数为求取联合分布函数提供了一条便捷的通道。

2.1.3　基于Copula理论的一致性和相关性测度

单调转换不变性定理:对随机变量(x1，…，xn，…，xN)作严格的单调增变换，相应的Copula函数不变，即若＞0，则Cx1，…，xn，…，xN= Ch1(x1)，…，hn(xn)，…，hN(xN)，其中Cx1，…，xn，…，xN表示连接(x1，…，xn，…，xN)的Copula函数，Ch1(x1)，…，hn(xn)，…，hN(xN)表示连接(h1(x1)，…，hn(xn)，…，hN(xN))的Copula函数。

Copula函数C中连续随机变量间的一致性测度和相关性测度的一个重要性质就来源于上述定理，即由Copula函数导出的相关性指标，是严格单调增变换下的相关性，比线性相关的范围要宽。所以下面介绍一致性和相关性测度。

1)一致性和相关性测度。

(1) Kendall秩相关系数τ。设(x1，y1)，(x2，y2)是独立同分布的向量，x1，x2∈x，y1，y2∈y，令

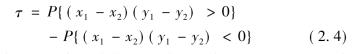
于是τ就度量了x与y变化的一致性程度。设(x1，y1)相应的连接函数是C(u，v)，Schwettzer和Wolff(1981)证明了τ可由相应的Copula函数给出:

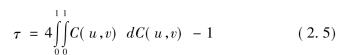
τ=1，表示x的变化与y的变化完全一致，所以正相关;

τ=－1，表示x的变化与y的反向变化完全一致，所以负相关;

τ=0，表示x的变化与y的变化一半是一致的，一半是相反的，所以不能判断是否相关。

(2) Spearman秩相关系数ρ。设(x，y)有联合分布H(x，y)，它们相应的边缘分布是F(x)和G(y)，x0∈x，y0∈y，且(x0，y0)～F(x)G(y)，即x0，y0独立。假定(x，y)与(x0，y0)也独立，令

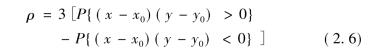
当(x，y)的Copula函数C(u，v)给定后，其中u= F(x)和v = G(y)，Schwettzer和Wolff(1981)证明了ρ可由相应的Copula函数给出:

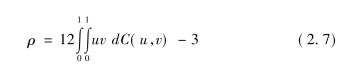
2)尾部相关测度。尾部相关系数是一个广泛应用于极值理论的测度，用来表示当一个观测变量的实现值为极值时，另一个变量也出现极值的概率。令X、Y为两个连续的随机变量，具有边缘分布F(·)、G(·)和Copula函数C(·，·)，那么上尾和下尾相关系数分别为:

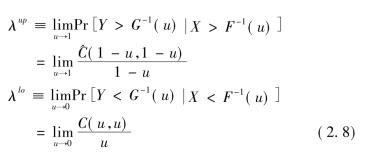
其中

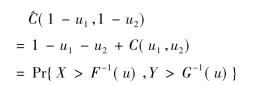
若λup(或λlo)存在且在区间(0，1］内，则随机变量X、Y上尾(或下尾)相关;若λup(或λlo)等于零，则随机变量X、Y独立。

可见，Copula有许多不同于相关系数的优点，特别是当对随机变量进行单调增或单调减的变换后，变量间的线性相关系数一般是不同的，而变量间的Copula是不变的。这在金融市场风险分析中可以理解为，若两支股票具有某种相关结构，尽管各自的股价在一定时期内发生了变化，但它们的关系不变，即它们之间的相关模式及相关程度不变，市场风险是不变的。另外，相关结构Copula中的参数与其他的一些相关性度量指标如Kendallpτ和Spearmanρ往往有一一对应关系，这对于度量金融市场资产间的相关性提供了方便。最后，引入相关结构Copula，可使投资者对市场的分析更加灵活。一般情况下不容易找到观测数据所服从的已知的联合分布，但是利用Copula方法就可以先对单个变量的数据所服从的分布进行估计，然后再找合适的相关结构，从而得到随机变量的联合分布。通过这样的分析，有助于对各资产的收益分布及资产间的相关关系有较明确的认识，这在风险分析中至关重要。

2. 2　商业银行安全可靠性分析

2.2.1　商业银行安全可靠度的界定

结构的可靠性定义为结构物(构件或系统)在规定的时间内，在规定的条件下，完成预定功能的能力。类似地，由于商业银行主要有四个职能:信用中介职能、支付中介职能、信用创造职能和金融服务职能。其中信用中介职能是最基本、本质的职能，而商业银行的首要和根本目的是生存和发展。因此可以定义金融机构的可靠性为该机构在规定时间和条件下完成如生存和盈利等预定功能的能力。完成各项功能的标志由极限状态来衡量，结构整体或部分在超过某状态时，结构就不能满足设计规定的某一功能的要求，这种状态称为结构的极限状态，极限状态是结构可靠和失效的界限。以本书所研究的银行为例(下文都只研究银行这种金融机构)，当银行资不抵债或不能清偿到期债务时，就将作出破产宣告，并依法将其财产进行清理、分配，这种行为称之为破产。结构的失效相当于银行的破产，所以银行资产刚刚等于负债的状态称之为银行的一种极限状态。

在可靠性分析中，极限状态一般由功能函数加以描述，当有n个随机变量影响可靠度时，功能函数为:

式中(x1，x2，…，xn)为银行的流动性指标，盈利性指标及安全性指标等基本随机变量。当z＞0时，银行处于可靠状态;当z= 0时，银行达到极限状态;当z＜0时，银行处于失效或者说破产状态。

银行的可靠性也可以用可靠度来度量，银行可靠度定义为在规定时间内，在规定的条件下银行完成预定功能的概率，也可称为安全概率，表示为PS。反之，如果银行不能完成预定的功能，则相应的概率称为银行的失效概率，或者称之为破产概率，表示为Pf。因为机构的可靠与失效为两个互不相容事件，所以银行的可靠概率PS与失效概率Pf互补，即

由于计算和表达上的方便，可靠度分析中也常用失效概率来度量可靠性。银行随机可靠度分析的核心问题是根据随机变量的统计特性和极限状态方程计算银行的失效概率。

实际上很难知道银行功能函数的概率分布，负债随机变量S和资产随机变量R的联合概率密度函数为fRS(r，s)。则随机点落入区域［r，r+ d r］和［s，s+ d s］所构成矩形区域的概率为fRS(r，s)d r d s。按概率理论银行失效概率可表示为:

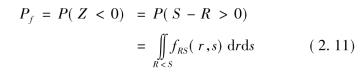
如果如R与S相互独立，则联合概率密度函数为fR(r) fS(s)，从而上式可写为:

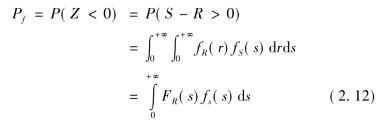
银行功能函数的概率分布取决于其包含的随机变量的概率分布和功能函数的形式。经典的银行失效概率表达式是一个高维积分，积分的维数与随机变量的数目相同。当随机变量的数目较多时，直接积分非常困难。

假定负债S和资产R独立且均服从正态分布时，式(2.11)可具体表示为

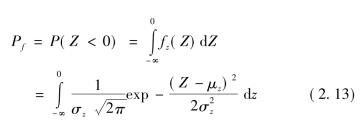
式中

其中μs，μr，和分别是负债S和资产R的均值和方差。

2.2.2　商业银行安全可靠度的计算方法

可靠度的计算方法分精确法和近似法两种，精确法是指按照公式(2.11)求解失效概率的方法，称全概率法。一般来说，负债S和资产R多为银行基本变量的非线性函数，这就需要根据众多基本变量的分布求出它们的均值和标准差，但这往往会遇到积分上的困难。精确法为一多重积分问题，因为一些基本变量很难确定其实际的概率分布，所以一般很难求得解析解。

近似法是指一次二阶矩计算方法等，虽然是近似的，但仍然属于概率法，称近似概率法。近似概率法将一个复杂的多重积分问题转化为一个简单的数值计算问题，计算效率高，尽管得出的失效概率带有一定的近似性，因其精度满足工程需要而在工程界被广泛应用，但在以银行为对象时则因精度不高而不能采用。

一次二阶矩法，根据功能函数的线性点的不同又分为中心点法和JC法等。中心点法的特点是首先对基本变量不做出分布类型假设，其次将非线性功能函数在随机变量的平均值(中心点)处作泰勒(Taylor)级数展开并保留至一次项，使之线性化，然后近似计算功能函数的平均值，求解可靠度。JC法适用于基本随机变量为任意分布下的可靠度指标的求解，其基本思路是:对非正态基本随机变量作当量正态化处理将其转换为等效正态随机变量，然后即可利用改进的一次二阶矩法求可靠指标。用一次二阶矩法求出的可靠度指标只有在正态分布和具有线性极限状态方程时才是精确的，否则只能得到近似的结果，而银行显然不符合这两个条件。

对于随机变量Xi相关的情况，必须采用正交变换法或改进的JC法。正交变换法的思路是对于相关变量可以先将它们变换为相互独立的随机变量，再用前面的一次二阶矩法求解可靠度指标和失效概率。将JC法作一些改进，能使之进行相关情况下的Hosofer－Lind可靠度指标计算而不用进行正态变换。值得提出的是，采用Copula函数拟合随机变量之间的相关模式和相关程度，可以将复杂的多重积分问题转化边缘分布的拟合和相关性的Copula拟合两个步骤，从而使得计算变得简单而且精度大大提高。

蒙特卡罗(Monte－Carlo)法，又称统计实验方法或随机模拟方法，是随着计算机的发展而逐步发展起来的一种独特的数值方法，它的基本思路是:先对影响可靠度的随机变量进行大量随机抽样，然后把这些抽样值一组一组地代入功能函数式，确定银行失效或破产与否，由此求得银行的破产概率。该方法的优点是回避了可靠度分析中的数学困难，不需考虑极限状态曲面的复杂性，但情景模拟仍有困难。

由于上述计算方法都有一定的不足，本书针对银行失效的本质特点，提出以下有所不同的计算模型。

1)单个银行破产风险计算模型。违约是指交易对手不能或不愿履行合同约定的条款而导致损失的行为。破产是在企业资不抵债或不能清偿到期债务时，作出破产宣告，并依法对其财产进行清理、分配的行为。可见违约和破产的概念有相似之处，违约风险和破产风险的本质特点都是资不抵债，由此类比信用风险的计算模型提出了破产风险计算的两类模型，进一步提出一种简化的计算方法。

(1)结构化模型。结构化模型给出了公司资产价值的基本假设，当公司资不抵债时发生破产。这类模型所研究的违约现象与公司的资本结构有关，因此称为结构化模型。把握结构化模型的关键是:模型所需的信息集Ft(As，Ls:s≤) t分别由公司资产价值At和违约障碍Lt构成。Merton(1974)提出的经典结构化模型假定公司资产价值服从非负的扩散过程:

式中，μ(t，At)是资产期望收益率，σ(t，At)是资产收益率的波动率，Wt是一个标准的布朗运动。

设时间t∈[0，T]，T为公司债务的到期日，若公司债务结构仅为面值为B，到期日为T的零息票债券，则T时刻公司的破产障碍和破产概率分别为LT= B和P(AT≤LT)，且在风险中性概率测度Q下，公司债券的价值为

式中，是折现因子，rt是无风险利率。

结构化模型的最大缺点是:现实中难以直接获取公司资产价值和资产收益波动率的基本数据，加之大多数公司的资本结构较为复杂，因此不可能为每项具体的公司债务进行定价。一个解决办法是模型收集历史破产数据，建立了一个大型数据库，通过历史破产经验分布来得到公司的破产概率。

(2)强度模型。该模型放弃了对公司资产价值的假设，将公司的破产现象视为服从Poisson过程(Poisson process)的随机事件，通过Poisson过程的特征参数——强度来刻画破产事件发生的可能性，即公司破产现象的发生取决于某些“风险”(hazard)的强度。强度模型放松了对公司资本结构的假设条件，且可采用可观测的市场数据进行破产风险定价。

强度模型所需的信息集Ft主要由破产时间τ构成，即Ft(τ，Xs:s≤t)。从数学的角度而言，破产时间是由一个强度为ht，依赖于d维状态变量Xt的Cox过程Nt=产生的停时。简单地说，Cox过程是一个点过程，该过程所需的信息集Ft(Xs:s≤t)由整个时间段内的状态变量Xt所生成。显而易见，这个过程就是强度为ht(Xt)的Poisson过程。

强度模型表达破产风险的形式简单，同时模型中的参数能够通过市场数据进行估计和校正，以适应市场的变化。

2)单个银行破产风险计算简化。近年来，我国利率改革进程不断加快。2000年，外汇业务存贷款利率、同业拆借利率等相继放开。2004年10月，人民银行放宽人民币贷款利率浮动区间，允许人民币存款利率下浮，人民币存款利率可在不超过各档次存款基准利率的范围内浮动，贷款利率原则上不再设定上限，中国利率改革进程进入与国际接轨的新阶段。利率成为同时影响银行的资产价值At和负债价值Lt最重要的因素，利率和资产、负债之间是明显的非线性关系。随着银行风险管理意识的提高，银行越来越注重影响银行安全的指标——不良贷款率。不良贷款率越高，直接说明银行资产的质量越差，银行发生破产的可能性越大。而且不良贷款率和存贷款利率也是密切相关的，当利率上升较快时，银行的不良贷款率通常也迅速上升，但是二者并不是绝对的线性相关。

在研究多因素导致结构破坏的可靠度分析模型时，工程结构中的研究成果大多数是采用二维正态分布模型来模拟材料因素、结构因素之间的联合分布，但正态分布模型需要对原数据进行正态化处理，而早在Jain和Singh(1986)的研究就指出了该处理方法往往不能保证处理后的数据一定呈正态分布。Gumbel(1960)指出实际研究表明许多工程或水文现象都服从极值分布中的Gumbel分布，例如洪峰流量和洪量。可见多因素联合分布拟合实施起来难度较大，通常需要对分布进行适当的假设，对模型进行一定的简化。本书在对银行破产风险进行建模时，如果同时考虑利率、不良贷款率、资产流动性比例、资本结构和资产负债期限匹配状态等多个因素，并且这些随机变量是相互关联的，则建模的实际可操作性很低。出于银行破产问题的复杂性，本书为了简化模型，仍然只考虑利率和资产负债期限匹配的缺口两个因素，并且假设这两个因素是相互独立的。

2. 3　系统可靠度Copula理论建模

2.3.1　串联型系统相关性可靠度

如果系统为串联型系统，其静态系统可靠度计算的一般表达式为

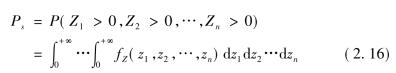
式中: Zi是第i个构件(机构)的功能函数，Zi=σi－Si，σi 和Si分别是第i个构件(机构)的资产(强度)和负债(应力)综合量; fZ(·)是(Z1，Z2，…，Zn)的联合密度函数。

对Ps的计算必须解决两个问题:一个是联合密度函数fZ(·)的确定非常困难，另外还有多重积分的繁琐性。而且由2.2节可知，构件的可靠度已经很难精确计算，要精确计算由多个构件形成的系统的可靠度Ps显得更加不太可能。一般情况下只能计算出Ps的上下界。

独立性假设理论不考虑相关性，即构件此时各自独立，此时有

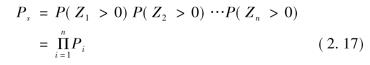
根据最薄弱环节理论，即认为零件功能函数是完全相关的两两线性关系:

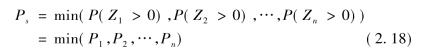
考虑到系统的实际相关结构，可以得到其可靠度的界为

上述不等式的实际含义:因为串联系统的可靠度Ps由最小寿命单元Xl= min(X1，X2，…，Xn)决定，机械系统中各零件失效之间的相互影响关系，由于承受共同载荷冲击，共同的外部工作环境等原因，多表现为正相关性。即在一定应力作用下，一个零件的强度会随着另一零件强度的衰减而衰减，从而导致其失效趋势比相互独立时要大，因而决定变量Xl受到另外n－1个存活变量Xi(i ≠l)的正相关性影响，使得Xl的存活概率比相互独立时要大。

n个单元X1，X2，…，Xn组成的串联型机械系统，设其相关结构Copula函数为Cn(μ1，μ2，…，μn)，则系统静态可靠度应为

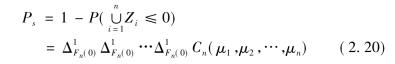
式中:“Δ”表示差分。

2.3.2　并联型系统相关性可靠度

并联系统由于正相关性影响，反而导致系统可靠度比在独立条件下要低。因为

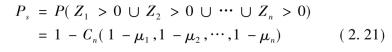
由正相关性可知

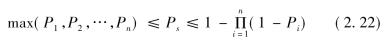
上述不等式的实际含义:并联系统可靠度由最长寿命单元Xh =max(X1，X2，…，Xn)决定，而决定变量Xh由于受到另外n－1个已失效变量Xi(i≠h)的正相关性影响，使得Xh趋于失效的概率比相互独立时要小。

2.3.3　相关性可靠度的Copula描述

不同结构关系的系统，其相关程度是介于独立不相关到完全线性相关的弱强连续变化的动态过程，进而导致串联型可靠度是，min(P1，P2，…，Pn)］的连续变化值，并联型系统可靠度则是［max(P1，P2，…，Pn)，1－(1－Pi)］的连续变化值。用Copula理论刻画机械系统中零件失效相关性，相关程度的变化连续性依赖于Copula模型中相关参数α的界值动态连续变化，可以实现系统可靠度的界值动态连续变化。

常用的正相关性Copula模型有:Gumbel Copula、正态Copula、Clayton Copula及Frank Copula。经过拟合效果的比较发现，最符合银行系统相关结构为Gumbel Copula函数。其分布函数为

似然函数

式中:m为样本容量; fi(·)是Xi的密度函数;cαj=。确定Copula模型中相关参数α的方法是，取历史数值或随机模拟值为随机样本，利用极大似然估计法进行估计。

2. 4　实例计算

2.4.1　样本数据与数据描述

我国的银行体系由3家政策性银行、4家国有商业银行、11家股份制银行、112家城市商业银行和众多的城市信用社、农村信用社及邮政储蓄信贷机构构成。从破产事件的发生对象看，国有银行、股份制银行和城市商业银行均存在倒闭的可能。国有商业银行的不良资产比重较大但存在政府的隐性担保，股份制商业银行的资产质量较好但是缺乏存款保险的保护，而政策性银行由于其特殊的融资方式、实施功能和政策背景一般不会发生破产，所以本书不将政策性银行作为研究对象。

出于问题研究的可操作性，本书没有将所有的银行都纳入研究，而是随机选择国内5家上市银行为样本银行，即中国银行、中国建设银行、民生银行、深圳发展银行、浦东发展银行。本书以2001年一季度到2008年中期为考察期，按季度采集资料。其中深发展考察期为1998年至2008年。本书选取的银行资产等数据来源于人民银行内部统计资料，与股市公开披露有差异则以公开披露的报表为准，市场利率及其波动率数据来自于聚源金融数据工作站。

2.4.2　变量选取

市场利率的确定是本节研究的一个重点。银行资产负债科目的调整一般是长期性市场行为，银行往往根据自身状况进行资金市场交易，市场利率是其进行资产负债管理决策的考虑重点。市场利率应当反映资金供求关系，该利率波动幅度对银行利息具有较大影响;所以此处应选取货币市场利率，而非央行所公布的存贷利率。

样本银行不同期限利率缺口数据来源于银行资产负债表和附注中流动性风险和利率风险表。

2.4.3　强度模型及估计结果

如前所述，为简化模型，在估计Possion分布的强度参数ht时，只考虑利率rt和资产负债期限匹配的缺口gapt两个因素，同时不考虑利率和资产负债期限匹配的缺口之间的相关关系，即认为二者是独立的。由此得到以下关于强度ht的简化模型:

其中，a和b为系数，c为常数(截距)项。为了估计上述模型的参数，还必须获得与利率rt和gapt对应期间的强度时间序列ht。由于强度ht和破产概率的正相关性，本书以各银行在相应期间使得该公司股价骤然下跌超过3%以上的事件次数(取对数)作为ht的代理变量。各银行可靠度计算所需的参数估计结果见表2－1。

表2－1　各样本银行可靠度

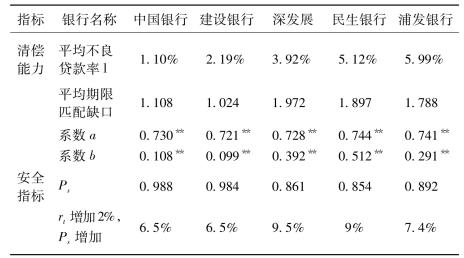
注:＊＊表示在5%显著性水平下显著，*表示在10%显著性水平下显著。

从表2－1首先可以发现，两个因素即利率和资产负债期限匹配缺口各自的系数a和b在5%的显著性水平下都显著为正，这说明当利率或资产负债期限匹配缺口增加时，破产强度h随之增加，由泊松分布的公式计算得到的可靠度减少，亦即破产风险增加。而从理论分析可知，随着利率市场化后利率增加，银行之间的竞争加剧，存贷款利差减少，同时不良贷款率也增加，银行的破产风险将会增加;另一方面，资产负债期限匹配缺口越大，银行的破产风险也越大。即利率或资产负债期限匹配缺口系数与破产风险是正向的相关关系。表2－1表明检验结果和理论分析是相吻合的。

系数a在各银行的估计值都比较大，但是在各银行的估计值相差却很小，这说明一方面利率变化对各银行安全性会产生较大的的影响，有可能导致破产风险;而另一方面利率变化对各银行破产风险的影响程度非常相近，利率风险对各银行来说是系统性风险。系数b在各银行的估计值都比较小，但是在各银行的估计值相差却很大，这说明资产负债期限匹配缺口变化对各银行安全性产生的影响相对要小，但资产负债期限匹配缺口变化对部分银行破产风险的影响程度仍然较大，例如深发展、民生银行的这种风险就偏大。

我国商业银行呈现全行业的“借短贷长”现象，商业银行的资产配置期限不断加长。一方面，我国商业银行的存贷比持续下降，在2008年基本上都满足75%的要求;考虑到我国存款将近年30%的增幅，实际上我国信贷资产的扩张是较快的，而且这种扩张往往是以中长期贷款业务的高速扩张作为基础。显然，银行信贷发放偏好于项目贷款和基建贷款等，而这些贷款往往期限较长，中长期资金运用挤占资金来源，短存长贷、长贷长占的现象必然出现，这些加重了中国银行业流动性风险和潜在利率风险。显而易见，如果这种资产负债期限缺口匹配失调，“借短贷长”现象趋势发展下去，随着利率市场化进程不断加快，必然会出现以下问题:

(1)利率市场化后，长时间升息周期或者频繁的利率波动将可能导致全行业的亏损，全行业资产负债期限匹配的缺口状态将导致银行之间无法对冲风险，全行业利润率将直接下降，资产收益率和权益收益率将不断下降。

(2)一旦遭遇经济波动，必然引发银行业的挤兑风潮，银行存款不再成为稳定的资金来源，银行流动性危机将导致破产风险。

根据表2－1的数据，如果不考虑利率管理水平等其他因素，当市场利率发生较大变化时，样本银行破产风险均会不同幅度上升，有三家银行破产风险上升幅度均超过7%以上，其中深发展受利率突变的影响最为突出，高达9.5%，其次是民生银行和浦发银行，分别为9%和7.4%。目前我国正处于利率市场化前期，银行面临的破产风险不能完全忽视。因此，各商业银行的利率风险管理任务异常艰巨，应及早制定相关措施，预防和化解利率骤变导致银行破产的风险。

要说明的是，上述模型的简化存在较大的模型风险。一种处理办法是模型中的参数可以通过经验分布或市场数据进行估计和校正，以适应市场的变化。

2.4.4　银行系统可靠度计算

银行系统中各银行失效关系符合正相关性，因此对于每一对银行之间的相关结构，选用正相关的Gumbel Copula进行拟合。经10000次数值仿真，样本值代入式(2.24)似然函数中，得到各银行失效的相关参数α的估计值，见表2－2。

从银行可靠度相关参数估计值可以看出，中国银行和深圳发展银行、民生银行和浦发银行之间的相关参数α相对最小，均在0.1左右;中国建设银行和深圳发展银行、民生银行和浦发银行之间的相关参数相对要大一些，α取值均在0.2以上;而深圳发展银行、民生银行和浦发银行之间的相关参数非常大，α取值均在0.8以上。由于α值越趋于0，表明两变量间的上尾相关程度越高。当α趋向于1时，CG(u，v;1)= uv，说明两变量相互独立。这说明虽然从表2－1得到深圳发展银行、民生银行和浦发银行各自的破产概率相对较大，但是其中的任何一家银行破产，传染给其他两个银行的可能性都非常小。而中国银行或者中国建设银行如果发生破产，深圳发展银行、民生银行和浦发银行受到传染也破产的可能性较大，相对而言，前者的传染程度更为显著。这些特征也间接地表明:中国银行的影响作用大于中国建设银行，中国银行处于中国银行体系的中心位置，而中国建设银行相对来说处于次中心位置。

表2－2　各银行可靠度相关参数的估计值

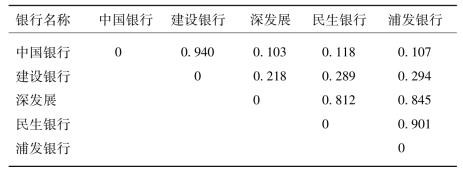
从表2－2还意外发现，中国银行和中国建设银行间的相关参数值非常大，这说明两家银行间几乎不会出现相互传染。原因可能是中国银行和中国建设银行间的资金流动较弱，或者两银行间的资金流相对于其自有资本数量较小，同时，中国银行和中国建设银行的自有资本均大于银行间资产和负债数量，从而割断了两银行间的传染渠道。

结合表2－1和表2－2的结果还可以发现清偿能力越大越不容易受到传染。深圳发展银行、民生银行和浦发银行的清偿能力最小，发生传染的概率最大;中国建设银行的清偿能力大，受到波及的概率最小。

由串、并联的可靠度计算模型式(2.20)和式(2.21)，可以计算出由各构件组成的单元或系统的可靠度。对于由本书研究的5个银行组成的系统可靠度，因为各银行的破产概率都比较小，同时各银行之间破产传染程度较小，类似机械系统中的并联结构，所以简化假设各银行之间是并联关系，计算得到这个系统的破产概率为0.0083，即可靠度为0.9917，接近于1，说明样本银行体系目前安全性较高。而如果采用独立性假设法得到Ps= 0.9985，由最薄弱环节法得到Ps= 0.9880。两者与考虑相关结构的系统可靠度0.9917均存在着一定的偏差。

2. 5　本章小结

本章在简单介绍Copula理论和可靠性理论的基础上，将结构系统的可靠度概念融入金融系统，构件的失效概率相当于金融机构的破产概率，结构系统的失效概率相当于金融系统的破产概率。首先，在对比了违约风险和破产风险的概念和本质特点基础上，类比信用风险的计算模型提出了破产风险计算的两类模型，进一步提出一种简化计算方法，并利用有限的数据进行了实证检验。然后，从银行失效相关结构角度，提出银行系统相关性可靠度计算研究的Copula方法。给出了银行系统可靠度的Copula计算模型，同时解决了相关性强弱程度的确定问题，保证了精度。最后，通过随机抽样样本银行系统的实例计算，说明该理论方法的可行性、有效性。