机械优化设计

在工业生产中，优化设计是随CAD技术的应用而迅速发展起来的一门现代设计学科，是企业在进行新产品设计时，追求具有良好性能、满足生产工艺性要求、经济性能好等指标的有效方法。优化设计提供了一种逻辑方法，在所有可行的设计方案中进行最优的选择，在规定的条件下得到最佳设计效果。目前，优化设计方法已广泛应用于各个工程领域，如飞行器和宇航结构设计，在满足性能的要求下使得重量最轻，使空间运载工具的轨迹最优；机械加工工艺工程设计，在限定的设备条件下使生产率最高等。优化设计作为一种先进的现代化设计方法，已成为CAD/CAM技术的一个重要组成部分。

机械优化设计包括建立优化设计问题的数学模型和选择恰当的优化方法与程序两方面内容。由于机械优化设计是应用数学方法寻求机械设计的最优方案，所以首先要根据设计的机械设计问题建立相应的数学模型，即用数学形式来描述实际设计问题：在建立数学模型时需要应用专业知识确定设计的限制条件和所追求的目标，确立设计变量之间的相互关系等。机械优化设计问题的数学模型可以是解析式、试验数据或经验公式。虽然它们给出的形式不同，但都反映了设计变量之间的数量关系。数学模型一旦建立，机械优化设计问题就变成一个数学求解问题。应用数学规划方法的理论，根据数学模型的特点，选择适当的优化方法，进而采用计算机作为工具求得最佳设计参数。

4.4.1 数学模型

1）设计变量

在产品设计中，一个设计方案可以用一组基本参数的数值来表示，这些基本参数可以是构件长度、截面尺寸、某些点的坐标值等几何量，也可以是质量、惯性矩、力或力矩等物理量，还可以是应力、变形、固有频率等代表工作性能的导出量。但是，对某个具体的优化设计问题，并不是要求对所有的基本参数都用优化方法进行修改调整。例如，对某个机械结构进行优化设计，一些工艺、结构布置等方面的参数，或者某些工作性能的参数，可以根据已有的经验预先取为定值。这样，对这个设计方案来说，它们就成为设计常数。而除此之外的基本参数，则需要在优化设计过程中不断进行修改、调整，一直处于变化的状态，这些基本参数称为设计变量，又称优化参数。

设计变量的全体实际上是一组变量，可用一个列向量表示：

x＝［x 1 x 2…xn］

称作设计变量向量。向量中分量的次序完全是任意的，可以根据使用的方便任意选取。一旦规定了这样一种向量的组成，则其中任意一个特定的向量都可以是一个“设计”。以n个设计变量为坐标组成的实空间称作设计空间。一个“设计”可用设计空间中的一点表示，此点可看成设计变量向量的端点（始点取坐标原点），称作设计点。

2）约束条件

设计空间是所有设计方案的集合，但这些设计方案有些是工程上所不能接受的（例如长度取负值等）。如果一个设计满足所有对它提出的要求，就称为可行（或可接受）设计，反之则称为不可行（或不可接受）设计。

一个可行设计必须满足某些设计限制条件，这些限制条件称作约束条件，简称约束。在工程问题中，根据约束的性质可以把它们分成性能约束和边界约束两大类。性能约束也称状态约束，反映设计对象的性能或状态要求。例如，选择某些结构必须满足受力的强度、刚度或稳定性等要求。边界约束是对设计变量的取值范围加以限制的约束。例如，允许选择的尺寸范围就属于边界约束。

约束又可按其数学表达形式分成等式约束和不等式约束两种类型，写成统一的格式为

等式约束要求设计点在n维设计空间的约束曲面上，而不等式约束要求设计点在设计空间中约束曲面g（x）＝0的一侧（包括曲面本身）。所以约束是对设计点在设计空间中的活动范围所加的限制。凡满足所有约束条件的设计点它在设计空间中的活动范围称作可行域，其余区域则为非可行域。可行域内的设计点称为可行设计点，否则称为非可行设计点。处于不等式约束边界上的设计点称为边界设计点，是该约束所允许的极限设计点。

3）目标函数

在所有的可行设计中，有些设计比另一些要“好”，如果确实是这样，则“较好”的设计比“较差”的设计必定具备某些更好的性质。倘若这种性质可以表示成设计变量的一个可计算函数，则可以考虑优化这个函数，以得到“更好”的设计。这个用来使设计得以优化的函数称作目标函数。用它可以评价设计方案的好坏，所以它又被称作评价函数，记作f（x），用以强调它对设计变量的依赖性。目标函数可以是结构质量、体积、功耗、产量、成本或其他性能指标。

建立目标函数是整个优化设计过程中重要的问题。当对某一个性能有特定的要求，而这个要求又很难满足时，若针对这一性能进行优化将会取得满意的效果。但在某些设计问题中，可能存在两个或两个以上需要优化的指标，这将是多目标函数的问题。目标函数是n维变量的函数，它的函数图像只能在n＋1维空间中描述出来。为了在n维设计空间中反映目标函数的变化情况，常采用目标函数等值面的方法。目标函数的等值面，其数学表达式为

f（x）＝c （c为一系列常数）

代表一族n维超曲面。如在二维设计空间中f（x 1，x 2）＝c，代表x 1－x 2设计平面上的一族曲线。

4）优化问题的数学模型

优化问题的数学模型是实际优化设计问题的数学抽象。在明确设计变量、约束条件、目标函数之后，优化设计问题就可以表示成一般数学形式。

求设计变量向量x＝［x 1 x 2…xn］T使

f（x）→min

且满足约束条件

利用可行域概念，可将数学模型的表达进一步简化。设同时满足

gj（x）≤0 （j＝1，2，…，m）和hk（x）＝0 （k＝1，2，…，l）

的设计点集合为R，即为优化问题的可行域，则优化问题的数学模型可简化成：

求x，使得

在实际优化问题中，对目标函数一般有两种要求形式：目标函数极小化f（x）→min和目标函数极大化f（x）→max。由于求f（x）的极大化和求－f（x）极小化等价，所以优化问题的数学表达式一般采用目标函数极小化形式。

4.4.2 问题的基本解法

求解优化问题可以用解析法或近似的数值法。解析法是把所研究的对象用数学方程（数学模型）描述出来，然后再用数学解析法求出优化解。但是，在实际情况中，优化设计问题的数学描述比较复杂，所以不便于甚至不可能用解析法求解出来；此外，有时对象本身的机理无法用数学方程描述，只能通过大量的试验数据用插值或拟合方法构造一个近似的函数表达式，再来求优化解，并通过试验来验证；也可以采用数值迭代法来求解：以数学原理为指导，用某个固定公式代入初值后反复进行计算，每次计算后，将计算结果代回公式，使其逐步逼近理论上的精确解，当满足给定精度要求时，得出与理论解近似的计算结果。

用数值迭代法进行优化设计的基本思路是：在设计空间选定一个初始点x（0），从这一点出发，按照某一优化方法所规定的原则，确定适当的方向s（0）与步长α（0）进行搜索，获得一个使目标函数值有所优化的新设计点x（1），然后再以x（1）点作为新的起点重复上述过程。这样依次迭代，可得到x（2），x（3）…x（k），x（k＋1）等设计点，最后求出满足设计精度要求的、逼近理论最优点的近似最优点x*。

点列｛x（k）｝的迭代公式的一般格式为

x（k＋1）＝x（k）＋s（k）α（k）

式中，x（k）为第k步迭代点，即优化过程中所得的第k次设计点；s（k）为从第k次设计点出发的搜索方向；α（k）为从第k次设计点出发，沿s（k）方向进行搜索的步长；x（k＋1）为从第k次设计点出发，以α（k）为搜索步长，沿s（k）方向进行搜索所得的第k＋1次设计点。

例4-1 平面四连杆结构的优化设计。平面四连杆机构的设计主要是根据运动学的要求，确定其几何尺寸，以实现给定的运动规律。

图4-2是一个曲柄摇杆机构。图中x 1、x 2、x 3、x 4分别是曲柄AB、连杆BC、摇杆CD和机架AD的长度。φ是曲柄输入角，ψ0是摇杆输出的起始位置角。这里规定φ0为摇杆的右极限位置角为ψ0时的曲柄起始位置角，它们可以通过x 1、x 2、x 3、x 4确定。通常规定曲柄长度x 1＝1，x 4＝5。

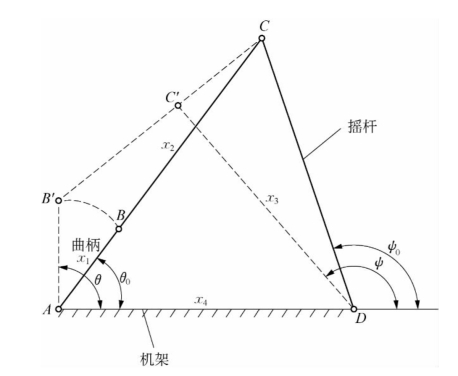
图4-2　曲柄摇杆机构

设计时，可在给定最大和最小传动角的前提下，当曲柄从φ0位置转到φ0＋90°时，要求摇杆的输出角最优地实现一个给定规律f 0（φ）。例如，要求

对于这样的设计问题，可以取机构的期望输出角ψ＝f 0（φ）和实际输出角ψj＝f j（φ）的平方误差积分准则作为目标函数，使

最小。

当把输出角φ取s个点进行数值计算时，它可以简化为

最小。

相应的约束条件如下。

（1）曲柄与机架共线位置时的传动角：

最大传动角：γmax≤135°；最小传动角：γmin≥45°

对本题可以计算出

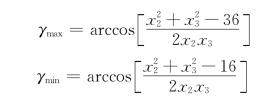
所以

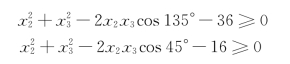
（2）曲柄存在条件：

（3）边界约束：

当x 1＝1时，若给定x 4，则可求出x 2和x 3的边界值。例如，当x 4＝0.5时，则有曲柄存在条件和边界值限制条件如下：

4.4.3 机械设计常用的优化方法

优化方法根据是否存在约束条件，可分为有约束优化和无约束优化；根据目标函数和约束条件的性质，可分为线性规划和非线性规划；根据优化目标的多少，可分为单目标优化和多目标优化等；根据求优方法的不同，可分为直接法和间接法等。图4-3为常用的优化设计方法。

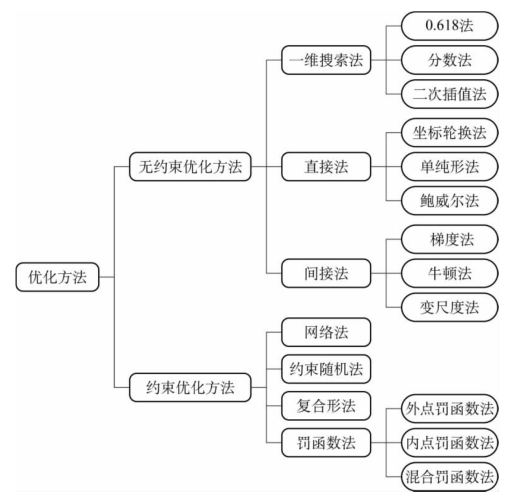
图4-3　常用优化设计方法

1）无约束优化方法

（1）一维搜索法。一维搜索法是优化方法中最基本、最常用的方法。所谓搜索，就是一步一步地查寻，直至区数的近似极值点处。其基本原理是区间消去法原则，即把搜索区间［a，b］分成3段或2段，通过判断去除非极小段，从而使区间逐步缩小，直至达到要求精度为止，取最后区间中的某点作为近似极小点。对于已知极小点搜索区间的实际问题，可直接调用黄金分割法（0.618法）、分数法或二次插值法求解。其中，黄金分割法步骤简单，不用求导数，适用于低维优化或函数不可求导数或求导数有困难的情况，对连续或非连续函数均能获得较好效果，实际应用范围较广，但效率偏低。二次插值法易于计算极小点、搜索效率高，适用于高维优化或函数连续的求导数情况；但程序复杂，有时可靠性比黄金分割法稍差。

①一维函数黄金分割法（0.618法）。黄金分割法是通过不断缩短搜索区间长度来确定极小点的方法。这种方法将搜索区间按比率β＝0.618缩小，直接计算目标函数f（x）的值确定取舍空间。这种算法的基本思路是在搜索区间［a，b］内取两点x 1、x 2，令x 1＝a＋（1－β）（b－a），x 2＝a＋（b－a）β。比较函数值f（x 1）、f（x 2）的大小：当f（x1）≥f（x 2）时，去掉区间［a，x 1］，搜索区间缩小为［x 1，b］；当f（x1）≤f（x2），去掉区间［x 2，b］，搜索区间缩小为［a，x 2］。这样反复计算比较、缩小区间，直至逐渐缩小的新区间［α，β］距离小于某一精度ε，即α－β≤ε，用同样的方法在新区间里选取两个点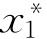、，令x*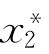＝（＋）/2为近似的最优点。

黄金分割法的效率不是最高的，但它具有较好的稳定性以及容易理解和便于使用等优点，故应用非常广泛。

②二次插值法（近似抛物线法）。二次插值法是一种一维优化方法，其基本思路是：在寻找函数f（x）极小值的区间内，利用三点函数值构造一个二次插值多项式φ（x）＝p 1 x 2＋p 2 x＋p 3来近似表达原函数f（x），并利用该函数的极值点技术代替原函数f（x）的最优点。当不满足精度要求时，按照一定规律缩短区间，并在新区间内重新构造三点二次插值多项式，再求其极值。如此反复，直到满足精度要求为止。

（2）直接法，主要有以下几种。

①坐标轮换法。坐标轮换法又称降维法。其基本思想是将一个“n维的无约束问题转化为一系列一维优化问题解决。基本步骤：从一个点出发，先令其他变量固定，选择其中一个变量相应的坐标轴方向进行一维搜索。当沿该方向找到极小点之后，再从这个新的点出发，对第二个变量采用相同的办法进行一维搜索。如此轮换，直到满足精度要求为止。若首次迭代即出现目标函数值不下降，则应采取相反的方向搜索。坐标轮换法的基本原理就是将一个n维的无约束最优化问题转化为一系列沿坐标轴方向的一维搜索问题来求解。该方法不用求导数，编程简单，适用于维数小于10或目标函数无导数、不易求导数的场合。但此法搜索效率低，可靠性差。

②鲍威尔法（Powell法）。鲍威尔法又称方向加速法，它直接利用函数值来构造共轭方向，利用共轭方向可以加速收敛的性质所形成的一种共轭方向法。该算法不用对目标函数求导数，属于直接最优化方法。其基本思想是不对目标函数作求导数计算，仅利用迭代点的目标函数值构造共轭方向。该方法具有二次收敛性，收敛速度快，可靠性也较好，是直接法中最有效的算法之一。适用于维数较高的优化问题，但编程较复杂。

（3）间接法，主要有以下几种。

①梯度法。利用函数的性态通过微分或变分求优的方法称为间接法。梯度法又称一阶导数法，是一种无约束优化的间接搜索法。其基本思想是利用目标函数值下降最快的负梯度方向作为寻优方向求极小值。梯度法需计算一阶偏导数，方法简单，可靠性较好，能稳定地使函数值下降。但当迭代点接近最优点时，收敛速度很慢。适用于目标函数存在一阶偏导数，精度要求不高的场合。

②牛顿法。牛顿法是梯度法的进一步发展。梯度法在确定搜索方向时，考虑了目标函数的一阶导数，在迭代点远离最优点时收敛速度快，但接近最优点时收敛速度极慢。而牛顿法进一步利用了二阶偏导数，从而大大加快了速度，且当迭代点接近最优点时收敛速度极快。其基本思想是把目标函数近似表示为泰勒展开式，并只取到二次项；然后，不断用二次函数的极值点近似逼近原函数的极值点，直到满足精度要求为止。该方法在一定条件下收敛速度快，尤其适用于目标函数为二次函数的情况，但计算量大，可靠性差。

③变尺度法（DRP）。变尺度法又称拟牛顿法，它在牛顿法的基础上又作了重要改进。变尺度法综合了梯度法和牛顿法的优点，使其迭代公式中的方向随着迭代点位置的变化而变化。在远离最优点时与梯度法的迭代方向相同，计算简单且收敛速度快。随着迭代过程的进行，不断修正迭代方向，来改善在最优点附近梯度法速度减慢的缺点。当迭代点逼近最优点时，利用牛顿法速度加快的点，迭代方向就趋于牛顿方向，因而具有更好的收敛性。这种方法是求解高维数（10～50）无约束问题的最有效方法。

2）约束优化方法

（1）复合形法。复合形法是一种在约束问题的可行域内寻求约束最优解的直接解法。其基本思想是：先在可行域内构造一个具有大于n＋1个顶点的初始复合形，然后对其各顶点函数值进行比较，判断目标函数值的下降方向，不断舍弃最差点而代之以既能使目标函数值有所下降，又能满足约束条件的新点，从而构成一个新的复合形。重复以上过程，新的复合形将不断向最优点移动和收缩直至达到一定收敛精度为止。该方法不需计算目标函数的梯度及二阶导数矩阵，计算量小，简明易行，工程设计中较为实用。但不适用于变量个数较多（大于15个）和有等式约束的问题。

（2）惩罚函数法（罚函数法）。罚函数法又称序列无约束极小化方法，适用于中、小型一般非线性约束优化问题。它是一种将约束问题转化为一系列无约束优化问题的间接解法。其基本思想是：将约束优化问题中的目标函数加上反映全部约束函数的对应项（惩罚项），构成一个无约束的新目标函数，即罚函数。根据新函数构造方法不同，又可分为：外点罚函数法、内点罚函数法和混合点罚函数法。

外点罚函数可以定义在可行域的外部，逐渐逼近原约束优化问题的最优解。该方法允许初始点不在可行域内，也可用于等式约束。但迭代过程中的点是非可行点，只有迭代过程完成后才收敛于最优解。

内点罚函数定义在可行域内，逐渐逼近原问题最优解。该方法要求初始点在可行域内，且迭代过程中任一解总是可行解，但不适用于等式约束。

混合点罚函数法是一种综合外点、内点罚函数法优点的方法。其基本思想是：不等式约束中满足约束条件的部分用内点罚函数，不满足约束条件的部分用外点罚函数，从而构造出混合罚函数。该方法可任选初始点，并可处理多个变量及多个函数，适用于具有等式和不等式约束的优化问题。但在一维搜索上耗时较多。

选择适用而有效的优化方法一般考虑以下因素：优化问题的规模；目标函数、约束函数的非线性程度、函数的连续性、等式约束和不等式约束以及函数值计算的复杂程度；优化方法的收敛速度、计算效率，稳定性、可靠性以及解的准确性等。