5.4 平面及直线与曲面立体相交
平面与曲面立体相交所得的截交线,一般情况下,是平面曲线或平面曲线和直线所组成的封闭图形,为截平面和曲面立体表面所共有。曲面立体截交线上的每一点,都是截平面与曲面立体表面的共有点。求出截交线上足够的共有点的投影,然后依次连接起来,便可得出截交线的投影。求共有点时,应先求作出截交线上特殊点的投影,如最高、最低点,最前、最后点,最左、最右点,可见与不可见的分界点,截交线本身固有的特殊点(如椭圆长、短轴的端点,抛物线顶点)等;如有必要再求一般点。
截交线是曲面体和截平面的共有点的集合。求作截交线的基本方法有素线法和纬圆法。
5.4.1 平面与圆柱相交
截平面与圆柱面的交线有三种情况,如表5-1所示。
表5-1 截平面与圆柱面的交线

例5-12 已知圆柱和截平面P的投影(见图5-26(a)),求截交线的投影,补作被截圆柱W面投影图。
分析 正垂面P与圆柱轴线倾斜,截交线为椭圆。该椭圆的V面投影积聚在PV上,H面投影位于圆柱面的投影圆周上已知。根据点的投影规律,即可求出截交线的W面投影。
作图 如图5-26(b)所示,先作出圆柱的W面投影,再求作截交线上若干个点的投影,用光滑的曲线连接各点,即为所求。

图5-26 例5-12图
(1)求特殊点。圆柱的V面投影轮廓线(最左、最右素线)与PV的交点a′、b′为椭圆长轴端点的V面投影,最前、最后素线的V面投影与PV的交点c′、d′为短轴端点的V面投影;由a′、b′和c′、d′可作出其W面投影a″b″和c″d″。
(2)求一般点。为使作图准确,需要再求截交线上若干个一般点。在H面投影圆周上取1、2、3、4点,根据投影规律作出其V面投影1′、2′、3′、4′,再作出W面投影1″、2″、3″、4″。
(3)在W面投影图中,用光滑的曲线依次连接各点成椭圆曲线,即为截交线的W面投影。
讨论 当截平面与圆柱轴线相交的角度发生变化时,其截交线椭圆在投影面上投影的形状,长、短轴方向及大小也随之变化。圆柱轴线处于铅垂位置时,正垂面截圆柱其W面投影如图5-27所示。图中c″d″长度不变,等于圆柱直径。当α<45°时,c″d″>a″b″,W面投影是以c″d″为长轴、a″b″为短轴的椭圆(见图5-27(a));当α=45°时,c″d″=a″b″,W面投影为圆(见图5-27(b));当α>45°时,a″b″>c″d″,W面投影是以a″b″为长轴、c″d″为短轴的椭圆(见图5-27(c))。
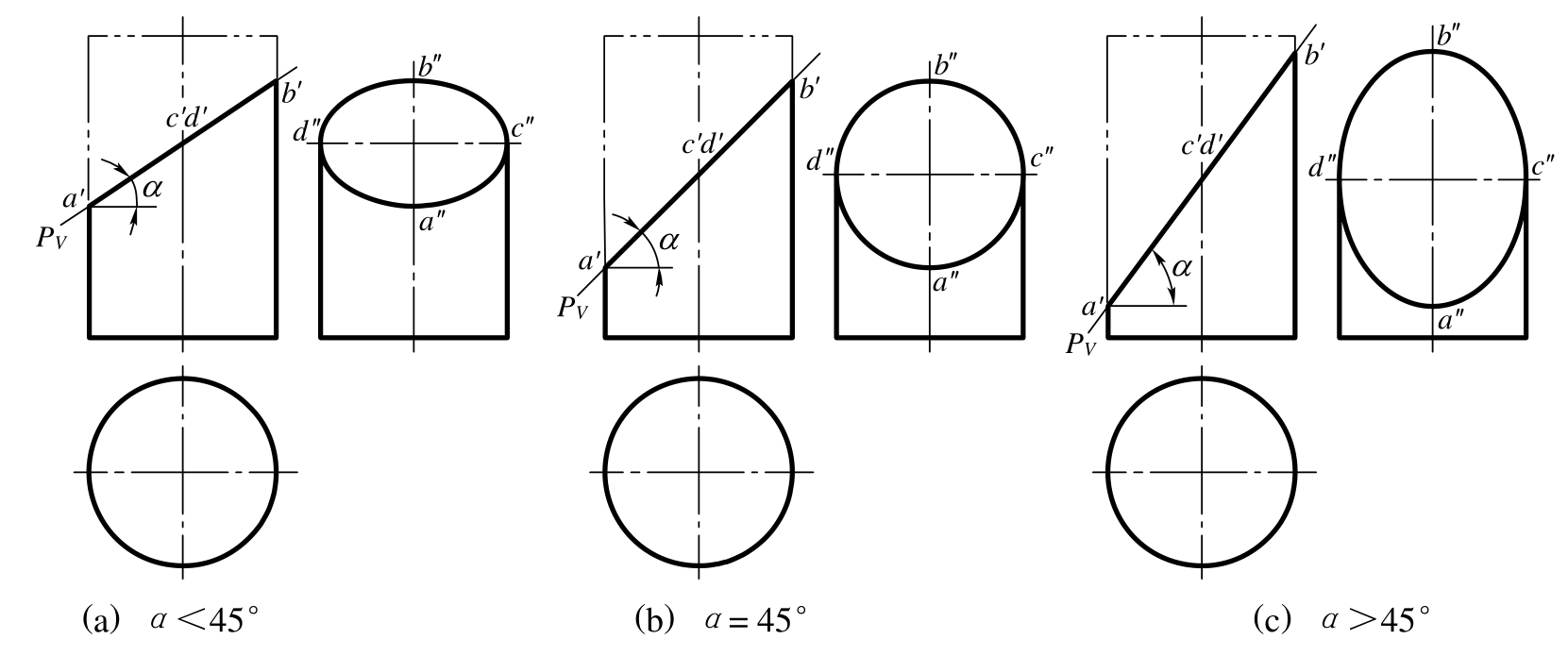
图5-27 截平面倾斜角度对截交线投影的影响
思考 圆柱轴线处于水平位置时,正垂面截圆柱其H面投影会是什么样呢?
例5-13 如图5-28(a)所示,已知切口圆柱的V面和W面投影,求作H面投影。

图5-28 例5-13图
分析 从给出的V面投影图可知,圆柱被水平截平面P和正垂截平面Q截割。水平截平面P与圆柱轴线平行,其截交线是与轴线平行的两条直素线,截交线的V面投影与PV重合,截交线的W面投影积聚成两点位于圆柱面的W面投影圆周上;正垂截平面Q与圆柱轴线倾斜,其截交线为大半椭圆,截交线的V面投影与QV重合,截交线的W面投影与圆柱面的W面投影圆周重合。截交线的V面和W面投影为已知,根据投影规律,即可求出H面投影。
作图 如图5-28(b)所示,先作出圆柱的H面投影,再求作截交线上若干个点的投影,用光滑的曲线连接各点,即为所求。作图步骤,请读者看图自行思考。
5.4.2 平面与圆锥相交
截平面与圆锥面相交时,由于截平面对圆锥轴线相对位置的不同,截交线有五种情况,如表5-2所示。
例5-14 如图5-29(a)所示,已知圆锥和截平面P的投影,求截交线的投影和断面的实形。
分析 由图5-29(a)可知,截平面P为正垂面。平面P与圆锥的所有素线相交,截交线为椭圆。平面P与圆锥最左、最右素线的交点,即为椭圆长轴的端点A、B。椭圆短轴垂直于V面,且垂直平分AB。截交线的V面投影重合在PV上,为已知;H面投影仍为椭圆。椭圆长短轴的投影仍为椭圆投影的长短轴。
作图 (1)求特殊点(见图5-29(b))。在V面投影上PV与圆锥V面投影轮廓线的交点a′、b′,即为长轴端点A、B的V面投影。AB的H面投影ab,就是椭圆投影的长轴。椭圆短轴CD的V面投影c′d′必积聚在a′b′的中点。过C、D作纬圆,或作素线SⅠ、SⅡ求出C、D的H面投影c、d。
(2)求一般点(见图5-29(c))。用纬圆法求作最前、最后素线与平面P的交点M、N和一般点E、F的H面投影m、n和e、f。
表5-2 截平面与圆锥面的交线

(3)在H面投影图中,用光滑的曲线依次连接各点成椭圆曲线,即为截交线的H面投影(见图5-29(d))。
(4)求断面实形。用换面法求出断面的实形(见图5-29(d))。

图5-29 例5-14图
思考 本题的W面投影怎样作图?
例5-15 如图5-30(a)所示,求正平面Q与圆锥的截交线。
分析 由于截平面Q为正平面,截交线的H面投影和W面投影积聚成为一条直线,分别与截平面Q的H面投影QV、W面投影QW重合。根据投影规律,可作出截交线的V面投影。
作图 如图5-30(b)所示,求出截交线上若干个点的投影,用光滑的曲线连接各点,即为所求。
(1)求特殊点。求作截交线上最高点Ⅰ的V面投影1′和最低点Ⅱ、Ⅲ的V面投影2′、3′。
(2)求一般点。用纬圆法求作一般点Ⅳ、Ⅴ的V面投影4′、5′。
(3)用光滑的曲线依次连接2′、4′、1′、5′、3′,即为截交线的V面投影。

图5-30 例5-15图
5.4.3 平面与圆球相交
平面与圆球相交,截交线是圆(见图5-31)。截交线在投影面上的形状取决于截平面相对于投影面的位置。当截平面平行于投影面时,圆截交线在该投影面上的投影,反映圆的实形;当截平面垂直于投影面时,圆截交线在该投影面上的投影为直线,长度等于截交线圆的直径;当截平面倾斜于投影面时,圆截交线在该投影面上的投影为椭圆。

图5-31 平面与圆球的截交
例5-16 如图5-32(a)所示,已知带切口半球的V面投影,求作H面和W面投影。
分析 半球的切口由一个水平截平面和两个侧平截平面组成,并对称于半球的对称面。水平截平面与半球的截交线为圆,在H面投影中反映圆的实形。侧平截平面与半球的截交线为半圆,在W面投影中反映半圆实形。

图5-32 例5-16图
作图 如图5-32(b)所示,求出截交线圆的半径R1和R2,在H面投影中,以R1为半径,以半球面的H面投影圆的圆心为圆心画圆,由投影规律“长对正”,得截交线的H面投影。在W面投影中,以R2为半径,以半球面的W面投影的圆心为圆心画半圆弧,由投影规律“高平齐”,得截交线的W面投影。两截平面的交线(是一段正垂线)在W面投影中不可见,应画成虚线。
例5-17 如图5-33(a)所示,已知球被正垂面P切截,求作被切截后球的H面和W面投影。

图5-33 例5-17图

续图5-33
分析 由于截平面P为正垂面,所以截交线是一个正垂圆。截交线的V面投影为直线,反映截交线圆的直径的实长。截交线的H面和W面投影为椭圆。
作图 利用球面上作点的方法作出椭圆上的若干个点。
(1)求作椭圆长、短轴的端点。如图5-33(b)所示,由截交线的V面投影可知椭圆长、短轴端点C、D、A、B的V面投影c′、d′、a′、b′,根据投影规律,作出c、d、a、b和c″、d″、a″、b″。
(2)求作球面轮廓线上的点。如图5-33(c)所示,由截交线的V面投影可知球面水平轮廓线上的点Ⅰ、Ⅱ的V面投影1′、2′,球面侧面轮廓线上的点Ⅲ、Ⅳ的V面投影3′、4′,根据投影规律,作出1、2、3、4和1″、2″、3″、4″。
(3)用光滑的曲线把各点连接成椭圆曲线,即为所求(见图5-33(d))。
5.4.4 直线与曲面立体相交
直线与立体表面的交点称为贯穿点,具有两个基本性质,即它是直线与立体表面的共有点,且它成对产生,一个贯入,一个穿出。求贯穿点的问题,实质上是求线面交点的问题。根据曲面体表面的投影或直线的投影有无积聚性,求作贯穿点投影的方法也不同。
1.积聚投影法求贯穿点
如果曲面体表面的投影或直线的投影具有积聚性,则贯穿点的投影在积聚性的投影中为已知,其余投影可利用表面上作点的方法求得。
例5-18 如图5-34(a)所示,已知直线与圆柱相交,求作W面投影和贯穿点。

图5-34 例5-18图
分析和作图 如图5-34(b),按投影规律,先作出圆柱及直线AB的W面投影。因为柱轴为铅垂线,柱面的H面投影积聚为圆,所以贯穿点M的H面投影m位于圆周上,由此可作出V面投影m′和W面投影m″。又因为圆柱的上、下底面为水平面,V面投影积聚为直线,贯穿点N的V面n′在此直线上,由此可作出H面投影n和W面投影n″。
图5-35是正垂线与圆锥相交。圆锥投影无积聚性,但直线AB的V面投影积聚为一个点a′(b′)。贯穿点M、N的V面投影m′、n′也积聚在这一点上。用在锥面上定点的方法(如纬圆法)可求得M、N的H面投影m、n。
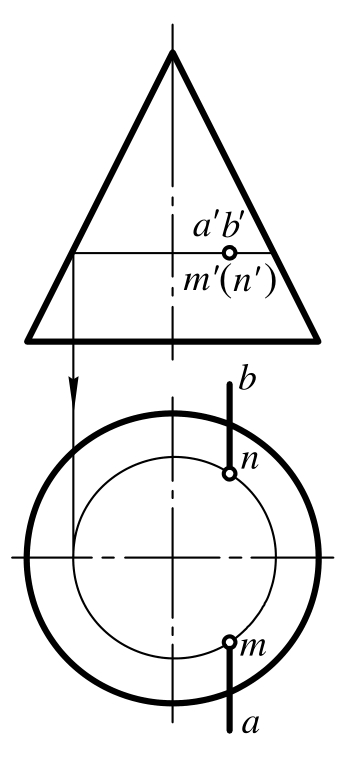
图5-35 正垂线与圆锥相交
2.辅助平面法求贯穿点
例5-19 如图5-36所示,求水平线MN与正圆锥的贯穿点。

图5-36 例5-19图
分析 圆锥面与水平线的投影均无积聚性,要求直线MN与圆锥面的贯穿点需借助于辅助平面。包含水平线MN作辅助水平面P,作出平面P与圆锥面的截交线圆,即可确定直线MN与圆锥的贯穿点。
作图 包含水平线MN作辅助水平面P,PV与m′n′重合,P平面与圆锥截交线的H面投影为一圆周,mn与圆周的交点k、l即为贯穿点的H面投影。由k、l可求得k′、l′。
例5-20 如图5-37所示,求直线AB与圆球的贯穿点。

图5-37 例5-20图
分析 如果包含直线AB作辅助铅垂面P,则平面P与圆球的截交线的H面投影与PH重合,V面投影为一椭圆,作图较为烦琐。为使作图简便,在本例中采用换面法求解。使新投影面V1与辅助铅垂面P平行,则平面P圆球截交线在V1面上的投影为一圆周。
作图 作新投影轴X1与PH平行,由此可在V1面上作出截交线圆的投影,a1b1与截交线圆的交点m1和n1即为贯穿点M和N在V1面上的投影,返回作图,即可作出贯穿点的H面投影m、n和V面投影m′、n′。
判断可见性 在V面投影中,m′可见,m′a′为实线;n′不可见,n′到球面轮廓的一段为虚线。在H面投影中,m可见,ma为实线;n不可见,n到球面轮廓的一段为虚线。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















