日间流动性风险测度模型

5.1.1 日间风险测度模型介绍

本书使用的流动性测度指标为杨朝军(2008)提出的价量结合的流动性综合测度指标Li:

其中，Li表示股票i的流动性，Ri表示股票i的收益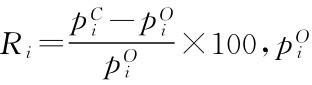，和分别表示给定时间段中股票i的开盘价格和收盘价格，相比Amihud(2002)的指标，该指标剔除了非交易时间新信息到来导致的股价变化。V(Pi，Qi)表示股票i的成交金额，Qi表示股票i的成交量，Pi表示股票i成交数量为Qi时的平均成交价格。

从该指标的构成分析，其本质是经过价格波动(用价格收益的绝对值衡量波动性)调整后的成交金额，表示股价波动1个百分点所需要的成交金额，指标的量纲为货币的计量单位。使用开盘价格与收盘价格计算的收益率可以较好地反映股票价格波动，因为开盘价格与收盘价格差额越小，则反映股价偏离开盘价格后重新回复到初始水平的弹性较大。

不可预期的流动性水平的波动即为流动性风险，类似于市场风险的测度，方差法是度量风险的最常用的方法。然而，样本方差只能测度一段时间的波动状况，基于样本方差测度的风险不能很好地反映风险的动态性与条件依赖性，条件方差是一种动态的方差测度方法，可以用来研究波动随时间演变的特征。金融时间序列往往存在条件异方差性(Conditional Heteroscedasticity)和波动聚集性(Volatility Clustering)，波动率可能在一段时间里持续较高，而在另一段时间里持续较低。同时正面消息和负面消息的冲击具有非对称效应，我们称之为“杠杆效应”，GARCH理论在处理这些金融变量中取得了较高的成效。在用GARCH理论构建我们的流动性风险测度之前，我们先介绍相关知识。

1)GARCH模型简介

自回归条件异方差(ARCH)模型(Engle，1982)是考察资产收益波动的一个有力工具，它通过对条件方差使用自回归方式设定一个线性函数形式来模拟这种不可观测的二阶矩的变化。尽管ARCH模型简单，但为充分刻画变量的波动率过程，往往需要设定很多滞后扰动项，而且估计时容易违背参数估计非负的限制条件，不能保证条件方差恒为正。Bollerslev(1986)将ARCH模型推广，得到广义自回归条件异方差模型，即GARCH模型，他通过在波动率方程中加入条件方差的滞后项替代了许多滞后扰动项，改善了估计效果。大量实证研究表明，金融时间序列往往具有条件异方差性、波动聚集性和概率分布的尖峰厚尾特性，而GARCH类模型却可以很好地捕捉这些特性。

下面将采用GARCH模型族捕捉流动性风险演变的动态性质。GARCH模型一般由两个方程组成，一个是条件均值方程，可用一个ARMA模型表示其均值过程，另一个是条件方差方程。若收益率r服从ARMA(m，n)-GARCH (p，q)，则模型如下:其中，{εt}是一个独立同分布的随机变量序列，均值为0，方差为1，α0＞0，αi≥0， (αi+βi)＜1(当i＞p时，αi=0；i＞q时，βi=0)条件保证了方差有限，否则方差将是发散的，这时需要用单位根GARCH(IGARCH(p，q))来刻画。为方便表述，称为GARCH项。αi反映前期冲击扰动对将来条件方差的影响，βi反映前期条件方差对将来条件方差的影响。(αi+βi)的经济学含义是它反映了经济波动的持续性，它的值越大，波动的持续性越强。当q=0时，式(5-2)就是一个纯粹的ARCH(p)模型，当式(5-2)中的p=1且q=1时，就是GARCH(1，1)模型。

2)GARCH模型的扩展——EGARCH

Nelson(1991)指出GARCH模型中为保证方差的非负性需要对系数的非负性施加约束，这将限制了条件方差的动态性。

Nelson的指数GARCH(EGARCH)模型中，条件方差以对数形式表示:

zt=εt/σt，服从标准正态分布，并且g(zt)=ωzt+λ(zt-2/π)，它是一个非对称的相应函数，可以刻画金融时间序列的杠杆效应。

通常假设扰动项服从正态分布，然而，对证券市场收益率序列的大量实证研究普遍发现，金融收益率序列一般不服从正态分布假设，而是有明显的尖峰、厚尾特征。为获得更为稳健的参数估计结果，需使用GED分布等来刻画残差项的厚尾性。假定εt服从广义误差分布(GED)，密度函数为:f(x)=其中，Γ(·)是Gamma函数，λ=[2(-2/ν)Γ(1/ν)/Γ(3/v)]1/2，当ν=2时，GED分布退化为正态分布。若在GARCH(1，1)模型中，假设扰动项服从GED，具体的对数似然函数形式为:

其中，θ表示待估计的参数集合；T表示观测点数；r表示GED的形状参数，取值在0到无穷大之间，r=2时GED就是标准正态分布，r＜2时GED是厚尾分布，r＞2时GED是瘦尾分布，Γ(·)是Gamma函数。

5.1.2 基于时变方差法的日间流动性风险测度

流动性风险是流动性水平未来的不确定性，是其偏离其均值的不可预测的变化，我们可以用方差的方法来对流动性风险进行刻画。然而，股票市场的成交金额大，而价格相对变化值较小，这导致按照流动性综合测度指标(5 1)式计算的流动性水平非常大，该序列通常是非平稳的时间序列，按照该指标计算的流动性水平的方差或标准差也很大；因此，我们在数据处理的过程中，通常对(5 1)式做对数差分的处理，即

DLt=ln(Lt)-ln(Lt-1) 　(55)

按照式(5-1)计算得出的流动性将与研究样本的规模成正比，通常规模大的公司，成交量大、流动性较高。采用方差法测度的流动性风险值也会比较大，这里进行了流动性差分的处理之后，可以将研究样本的规模因素剔除，这样得到的流动性风险值便于不同规模的资产之间进行比较。

采用样本方差方法衡量风险有一定的局限性，因为该方法是基于过去一段时间数据计算得出的方差，这与风险的动态性特征不符。Bollerslev(1986)提出了广义条件异方差(GARCH)模型，该方法是一种条件方差测度，它可以动态的测度一个投资组合每天的风险情况。常用的ARMA(m，n)-GARCH(p，q)模型可以很好的反映平稳序列的自相关性和波动性的时变性，该模型由两部分组成，即分别是均值方程与方差方程。

其中，式(5-6)是均值方程，表明Xt序列服从ARMA(m，n)过程，标准残差Zt是0均值、单位方差的白噪声序列，残差εt互不相关。式(5-7)是方差方程，ht表示条件方差，表明条件方差不仅依赖于过去的条件方差，还依赖均值方程过去的残差值，αi≥0、βi≥0，如果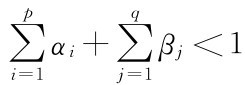，则表明条件方差序列是平稳的。这里如果Xt代表流动性变化率序列DLt，按照这种方法得出的条件方差序列ht，可用来表示研究样本在第t天的流动性风险，该值是时变的，我们可以计算出T时间内任何一天的流动性风险值。