探索勾股定理

第七节　探索勾股定理^[7]

《全日制义务教育数学课程标准（实验稿）》强调“数学课程应帮助学生了解数学在人类发展史中的作用”，因此在数学内容的学习过程中应该向学生介绍有关的数学背景知识，比如介绍欧几里得《原本》，使学生初步感受几何演绎体系对数学发展和人类文明的价值；介绍勾股定理的几个著名证法（如欧几里得证法，赵爽证法等）及其有关的一些著名问题，使学生感受数学证明的灵活、优美与精巧，感受勾股定理的丰富文化内涵。“探索勾股定理”是张维忠教授在浙江省金华市南苑中学开展的“基于数学文化的中学数学教学模式构建与实践”行动研究中的一个典型案例，这一教学研究成果曾于2012年6月荣获浙江省人民政府颁发的基础教育教学成果二等奖。

一、教学过程

（一）创设情境，提出问题

（幻灯片展示）《九章算术》中的一道题：“今有池方一丈，葭生其中央，出水一尺。引葭赴岸，适与岸齐，问水深、葭长各几何？”

师：在中国古代有一部经典之作叫《九章算术》，里面收录的都是关于测量计算之类的数学题目，我们来看其中一道有趣的题目。这道数学题翻译成现代文就是说：有一个边长为一丈的正方形水池，在池的正中央长着一根芦苇，芦苇露出水面1尺。若将芦苇拉到池边中点处，芦苇的顶端恰好到达水面。问水有多深？芦苇有多长？怎么解决呢？

学生思考，但大多露出迷茫的神情。

师：（提示）这是一个文字题，为了方便解决问题，我们最好把它改编成我们熟悉的数学问题。

（幻灯片展示）如图（图3-7-1），CD＝10，F为CD的中点，GE⊥CD，GF＝1，EC＝GE，求CE和CB。

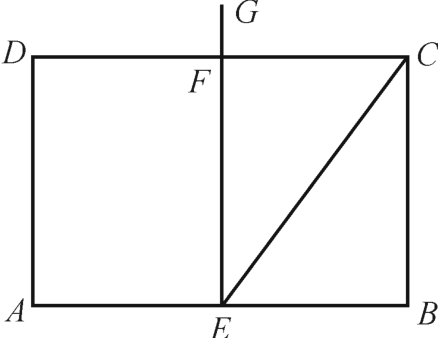
图3-7-1

师：怎么求解这道数学题呢？可以从哪里入手？学生仔细观察，小声讨论，但没有同学举手发言。

师：看来大家有点困难，那我们可不可以把要求的CE设为x，那么EF＝x－1，F是CD的中点，那么CF＝5，而GE⊥CD，因此我们已经把Rt△CEF的三边都表示出来了。我们只要知道这三边之间的关系，就能把x解出来了，那直角三角形三边之间有什么关系？

【评析】　课题的导入选用了《九章算术》的一道利用勾股定理求解的题目，使学生在学习数学知识的同时又能初步了解中国古代数学成就，在分析题目的过程中着重进行从文字语言到数学语言的过程，对培养学生的一般解题思路有一定的帮助。另外突出直角三角形三边关系这一研究方向，使学生感到原有知识的欠缺，可以很好地激发了他们的求知欲，这为下一步的探究活动做了精神上的准备。

（二）动手操作，探索新知

师：为了研究一般直角三角形三边之间的关系，我们不妨先来看看几个特殊的直角三角形。大家前后四个同学为一小组，动动手，按以下要求画几个直角三角形，并量出斜边的长度，看看哪个小组做得又快又好。

（幻灯片展示）做一个直角三角形，使两条直角边分别为a，b，并量一下斜边c的长度。

（1）a＝3cm，b＝4cm；（2）a＝6cm，b＝8cm；（3）a＝5cm，b＝12cm。

学生四人为一小组，其中三人分别作图测量，另一人记录。教师巡视中，发现部分学生的作图习惯不好，及时指出纠正错误。

师：请几个同学汇报一下作图测量的结果。

（学生踊跃回答，教师统一答案后，以图表的形式在幻灯片上显示）

师：大家仔细观察一下这几个直角三角形三边长，有发现什么规律吗？

生1：（马上回答）3²＋4²＝5²。

师：很好，其他同学有没有发现什么呢？

显然，该学生有预习过，在他的提示下，其他同学也得出了相应的结果。教师总结答案，填入表格。

【评析】　此环节按照浙教版教材进行设计，采用合作学习的形式，使学生在相互协助的过程中培养良好的合作习惯，同时也培养了学生认真作图的习惯及一定的动手操作能力。另外类似于比赛一样的形式，可以充分调动学生的积极性。

师：刚才我们利用了把边长平方这个办法，大家都知道正方形面积刚好就是边长的平方，那么让我们来看看一种情况，边长为3、4、5的直角三角形。

课件展示（图3-7-2），分别以直角三角形的边长向外作正方形，然后将它们分割成单位面积的小正方形，经过移动、割补，形成大正方形。（在此过程中学生普遍表现出兴奋之情）

图3-7-2

【评析】　借助多媒体设备生动形象的演示成功验证学生们的发现，让学生感到惊奇不已，同时也为后面运用面积法的思想来证明勾股定理做好了心理准备。

（三）自主探索，发现新知

师：我们通过图形变换的方法验证了3²＋4²＝5²，也就是说，直角三角形两直角边的平方等于斜边的平方，那么是不是任何直角三角形都有这样的规律呢？

回答声此起彼伏，部分学生回答认为，但不少学生不敢确认而保持沉默。

师：我们可不可以大胆猜想直角三角形都就有这样的规律？

生：（集体回答）可以。

师：那我们就猜想直角三角形两直角边的平方等于斜边的平方，猜想之后要做什么？

生：求证。

师：好，让我们来试试看。

（幻灯片展示）已知：在Rt△ABC中，∠C＝90°，AB＝c，BC＝a，CA＝b，求证：a²＋b²＝c²。

师：怎么证呢？从什么入手？

学生思考，但是基本上没有思路。

师：（提示）大家观察一下，以前有没有学过与a²＋b²有关的内容？

生2：两个正方形面积和。

师：对，这个刚才我们已经讲到了，还有吗？与平方有关的……

生3：(a＋b)²＝a²＋2ab＋b²。

师：这是我们在七年级下学过的知识点，看来大家掌握得还不错。

教师分析：a²＋b²＝(a＋b)²－2ab＝（b－a）²＋2ab＝c²，而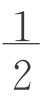ab就是直角三角形面积，所以只需要证明（a＋b）²－4× ab＝（b－a）²＋4× ab＝c²。

师：通过以上的分析，我们发现四个直角三角形与以c为边长正方形存在某种关系，那么大家能不能用四个直角三角形拼出一个以c为边长正方形呢？请同学们拿出课前发给大家的三角形，仍以刚才的小组形式，动手拼拼看。

学生们动手操作，尝试各种组合拼图，一开始成功的不多。教师在巡视过程中不断强调要使直角三角形的斜边刚好变成正方形的边。3分钟之后，有1/3小组已经拼出图形，教师进一步鼓励寻找其他方法，5分钟后有少数小组找到两种方法，纷纷举手要求发言。

教师邀请两位学生上讲台展示拼图结果（图3-7-3、图3-7-4）。

图3-7-3

图3-7-4

（幻灯片动态展示拼图过程）

【评析】　对于初二的学生来说，让他们完全靠自己的能力去寻找证明勾股定理的方法是很难的。因此教师需要进行一步步的引导，指出用四个直角三角形，以及利用面积法可以证明猜想。然后让学生通过动手操作，开展探索活动，这样的过程显得自然很多。

师：我们已经找到两种拼图的方法，那怎样利用这些图形来证明我们的猜想呢？

生4：面积相等。

师：好，能不能解释一下？

生4：第一种拼法中大正方形是由一个小正方形和四个直角三角形拼成，大正方形面积可以用边长来算，就是c²，另外还可以把小正方形面积和四个直角三角形面积加起来，就是（b－a）²＋4×ab。两种计算得到的结果应该是一样的，最后化简就可以得到：a²＋b²＝c²。

师：完全正确，对于第二种拼法，也是大正方形套小正方形，只是大正方形的边长变成了a＋b，小正方形边长是c，然后利用面积相等也可以证得a²＋b²＝c²。

【评析】　通过教师的启发诱导，从猜想到拼图操作，最后在通过计算验证猜想，学生经历了一次完整的探究活动，这个活动是在其原有的知识结构上展开的，在探究活动中渗透了面积的割、补、拼等重要方法，对培养学生的探究能力有很大的帮助。

（四）总结新知，展示背景

师：通过拼图和面积法，我们已经成功地证明了先前的猜想，就是任何直角三角形两条直角边的平方和等于斜边的平方，我们把这个结论叫做勾股定理，这个定理在数学史上有着举足轻重的地位。

（幻灯片展示）

教师介绍勾股定理名字的由来，展示勾股定理的三种证法，赵爽弦图证法、毕达哥拉斯证法及总统证法（图3-7-5），较为详细地介绍总统证法的证明过程，然后简单介绍勾股数和勾股树等相关内容。

图3-7-5

【评析】　通过介绍赵爽弦图证法使学生们感受到中国古代数学的伟大成就，激发了学生的成就感，而通过总统证法，学生们体会到了勾股定理证明方法的多样性与精巧性，无穷无尽的勾股数和美丽多姿的勾股数进一步引起学生们对数学学习的兴趣，感受到了数学的美。

（五）应用新知，解决问题

（幻灯片展示）

（1）已知△ABC中，∠C＝Rt∠，BC＝a，AC＝b，AB＝c。

①若a＝1，b＝2，求c；

②若a＝15，c＝17，求b。

学生思考，单独作答，教师板书示范解答过程。

（2）已知直角三角形中有两条边3和4，求第三条边。（图3-7-6）

【评析】　第（1）题是强调公式变形，明确定理使用的前提是要有直角三角形，结论必须是两直角边的平方和等于斜边的平方。第（2）题旨在考察学生的分类思想意识，强调在直角三角形中边不明确的情况下，应注意较大的边可以是直角边，也可以是斜边，培养学生思维的科学性和严密性。

图3-7-6

（3）一个长方形零件图（图3-7-7），根据所给的尺寸（单位mm），求两孔中心A、B之间的距离。

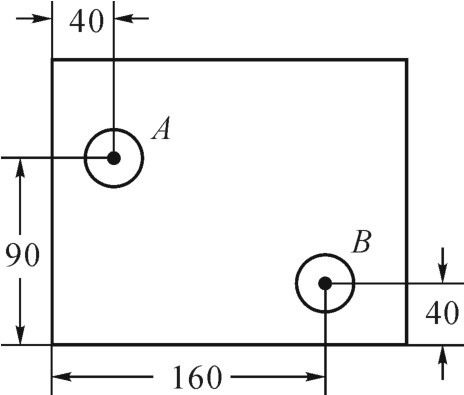
图3-7-7

（4）本节课引入时的芦苇问题。

【评析】　第（3）题是教材上的例题，解决问题的关键在于构造出含所求线段的直角三角形，然后用勾股定理进行求解。芦苇问题的解决要求先把具体的生活问题抽象成为数学问题，然后设要求的值为未知数，最后根据勾股定理建立方程，然后求解方程，期间渗透了数学的多方面思想，对学生的认知能力要求很高。学生通过求解此类题目能够体会到，数学来源于现实生活，应用于现实生活，并且培养了他们的数学应用意识和初步的数学建模思想。

二、课后反思

勾股定理的是公认的最重要的数学定理之一，几乎是全世界中学数学课程中都介绍的内容，通过不同文化背景的证明方法，学生能够体会到数学的文化价值。另外，勾股定理的教与学也是数学教育改革的晴雨表，具有极好的教育价值。

本节课的教学设计强调了数学的背景知识，采用探究活动的教学方式，从各方面达到符合数学新课程理念的要求，以下从几个方面来谈谈笔者的教学感受。

课程标准建议通过介绍有关的数学背景知识使学生对数学的发展有所了解，激发学生学习数学兴趣。而事实上，历史文化来丰富数学教学和数学学习，一个直接的办法就是让学生去解一些早期数学家感兴趣的问题。因此本节课用一道《九章算术》中的题目贯穿整节课，让学生在解决源于数世纪以前的问题时经历某种激动和满足。同时，在利用赵爽弦图证法得出勾股定理之后还补充介绍了毕达哥拉斯证法及总统证法，进一步向学生展现了不同文化背景下的数学思想，即中国古代数学文化传统具有“寓理于算”，建立在不证自明、形象直观的原理上；而西方的证法反映的是严谨的逻辑和理性的推理，展示的是对数学美和数学理性的追求。

新课程提倡探究式教学，给予学生自主的空间，尽可能让学生经历、体验探究活动的过程，并在此基础上获得数学知识，积累数学活动经验，掌握数学技能，领悟数学思想方法，体验数学情感。本节课把教学过程设计成学生对知识再发现、再创造的过程，定理的引入从特殊到一般，让全体学生参与实验操作、观察猜测、探索结论过程。在教学过程中引导学生大胆猜想，这符合现代教学理论中“要把学生学习知识当做认识事物的过程来教学”的观点。

本节课做到了让学生带着问题学习，让学生动手操作：画、剪、拼、凑图，既有独立思考，又有分组讨论交流，充分体现了学生的主体地位，体现了“以学生发展为本”这一课改的指导思想。在探索勾股定理的过程中，即培养了学生的数学直观能力，启迪了学生的探索灵感，又体现了教学的针对性、活动性、开发性、合作性，创造了一个激发学生积极思维、解决问题的学习氛围。

参考文献

［1］教育部．全日制义务教育数学课程标准（实验稿）［M］．北京：北京师范大学出版社，2001．

［2］范良火等．义务教育课程标准实验教科书数学（八年级上册）［M］．杭州：浙江教育出版社，2005．

［3］张维忠．文化视野中的数学与数学教育［M］．北京：人民教育出版社，2005．

［4］姚志敏，许芬英．勾股定理的再发现——一堂数学研究课几个片断的教学与评析［J］．中学数学教学参考（初中），2006（3）：6－8．

［5］许国华，施洪康．“勾股定理”教学设计与评析［J］．中学数学教育（初中教师版），2004（4）：22－23．