几何学和经验

为什么数学比其他一切科学受到特殊的尊重，一个理由是它的命题是绝对可靠的和无可争辩的，而其他一切科学的命题在某种程度上都是可争辩的，并且经常处于会被新发现的事实推翻的危险之中。尽管如此，要是数学的命题所涉及的只是我们想象中的对象而不是实在的客体，那么别的科学部门的研究者还是没有必要去羡慕数学家。因为，如果人们已经同意了基本命题（公理），以及由此导出其他命题的方法，那么，毫不奇怪，不同的人必定会得出同样的逻辑结论。但是数学之所以有高声誉，还有另一个理由，那就是数学给予精密自然科学以某种程度的可靠性，没有数学，这些科学是达不到这种可靠性的。

在这里，有一个历来都激起探索者兴趣的谜。数学既然是一种同经验无关的人类思维的产物，它怎么能够这样美妙地适合实在的客体呢？那么，是不是不要经验而只靠思维，人类的理性就能够推测到实在事物的性质呢？

照我的见解，这问题的答案扼要说来是：只要数学的命题是涉及实在的，它们就不是可靠的；只要它们是可靠的，它们就不涉及实在。我觉得，只有通过那个在数学中叫做“公理学”（axiomatics）的趋向，这种情况的完全明晰性才成为公共财产。公理学所取得的进步，在于把逻辑-形式同它的客观的或者直觉的内容截然地划分开来；依照公理学，只有逻辑-形式才构成数学的题材，而不涉及直觉的或者别的同逻辑-形式有关的内容。

我们暂且从这个观点来考查几何学的任何一条公理，比如：通过空间里的两个点，总有一条而且只有一条直线。这条公理，在古老的和近代的意义上是怎样解释的呢？

古老的解释：大家都知道什么是直线，什么是点。这种知识究竟是来自人类的一种精神能力还是来自经验，是来自这两者的某种结合还是来自其他来源，这不是由数学家来决定的。他把这问题留给哲学家。上述这条公理，是以这种先于一切数学的知识为依据的，它像别的一切公理一样，是自明的，就是说，它是这种先验知识的一个部分的表述。

近代的解释：几何学所处理的对象是以直线、点等等这类词来表示的。对于这些对象并不需要假定有任何知识或直觉，而只是以公理（如上述的那样一条公理）的有效性为前提，这些公理是在纯粹形式意义上来理解的，即丝毫没有任何直觉的或经验的内容。这些公理是人的思想的自由创造。几何学的其他一切命题都是公理的逻辑推论（这里公理只是从唯名论的意义上来理解的）。几何学所处理的对象是由公理来定义的。施利克（Schlick）因此在他的一本关于认识论的书中，非常恰当地把公理说成是“隐定义”。

现代公理学所提倡的这种公理观点，清洗掉数学中一切外附的因素，因而也驱散了以前笼罩着数学基础的那团神秘的疑云。但是这样一种修正了的对数学的解释，也弄明白：这样的数学，对于我们的直觉对象或者实在客体，不能作出任何断言。在公理学的几何中，“点”、“直线”等词只不过代表概念的空架子。至于给它们以什么内容，那是同数学无关的。

然而另一方面也是确定无疑的，一般地说来，数学，特别是几何学，它之所以存在，是由于需要了解实在客体行为的某些方面。几何（Geometrie）这个词本来的意思是大地测量，就证明了这一点。因为大地测量必须处理某些自然对象（即地球的某些部分、量绳、量杆等）彼此之间各种排列的可能性。仅有公理学的几何概念体系显然不能对这种实在客体（以后我们称之为实际刚体）的行为作出任何断言。为了能够作出这种断言，几何学必须去掉它的单纯的逻辑形式的特征，应当把经验的实在客体同公理学的几何概念的空架子对应（coordination）起来。要做到这一点，我们只要加上这样一条命题：固体之间的可能的排列关系，就像三维欧几里得几何里的形体的关系一样。这样，欧几里得的命题就包含了关于实际刚体行为的断言。

这样建成的几何学显然是一种自然科学；事实上我们可以把它看作是一门最古老的物理学。它的断言实质上是以经验的归纳为根据的，而不单单是逻辑推理。我们应当把这样建成的几何学叫做“实际几何”，下面还要把它同“纯粹公理学的几何”区分开来。宇宙的实际几何究竟是不是欧几里得几何，这个问题有明白的意义，其答案只能由经验来提供。如果人们运用光是沿直线传播的这条经验定律，而且事实上光是以实际几何意义上的直线在传播的，那么物理学中一切长度的量度就构成了这种意义上的实际几何，测地学和天文学上的长度量度也是如此。

我特别强调刚才所讲的这种几何学的观点，因为要是没有它，我就不能建立相对论。要是没有它，下面的考虑就不可能：在相对于一个惯性系转动的参照系中，由于洛伦兹收缩，刚体的排列定律不符合欧几里得几何的规则，因此，如果我们承认非惯性系也有同等地位，我们就必须放弃欧几里得几何。要是没有上述解释，就一定作不出向广义协变方程过渡的决定性的一步。如果我们不承认公理学的欧几里得几何的形体同实在的实际刚体之间的关系，那么我们就容易得出如下的观点，这就是那位敏锐的、深刻的思想家彭加勒（H．Poincaré）所主张的观点：欧几里得几何以其简单性突出地胜过其他一切可想象的公理学的几何。现在因为公理学的几何本身并不包含关于能被经验到的实在的断语，而只有在同物理定律结合时才能做到这一点，所以不管实在的本性如何，要保留欧几里得几何，应当是可能的，而且也是合理的。因为，要是理论同经验之间出现了矛盾，我们宁愿改变物理定律，而不愿改变公理学的欧几里得几何。如果我们拒不承认实际刚体同几何之间的关系，那么我们就确实难以摆脱这样的约定，即认为欧几里得几何应当作为最简单的几何而被保留下来。

彭加勒和别的研究者为什么拒不承认实际刚体同几何体之间的等效性（这种等效性是很容易想到的）呢？那只是因为经过讲一步的考查后，才知道自然界里实在的固体并不是刚性的，因为它们的几何性状（即它们相对排列的各种可能性）是取决于温度、外力等等的。这样，几何同物理实在之间的原始的、直接的关系显然被破坏了，我们不得不倾向于下面这个更一般的观点，这是彭加勒观点的特征。几何（G）并不断言实在事物的性状，而只有几何加上全部物理定律（P）才能做到这点。用符号来表示，我们可以说：只有（G）＋（P）的和才能得到实验的验证。因此，（G）可以任意选取，（P）的某些部分也可以任意选取；所有这些定律都是约定。为了避免矛盾，必须注意的只是怎样来选取（P）的其余部分，使得（G）和全部的（P）合起来能够同经验相符合。从这个角度来考虑，公理学的几何同已获得公认地位的那部分的自然规律，在认识论上看来是等效的。

我认为，从永恒的观点来看（sub specie aeterni），彭加勒是正确的。相对论中量杆这个观念以及同它搭配的时钟这个观念，在实在世界里找不到它们的确切对应的东西。也很明显，固体和时钟在物理学的概念大厦里所扮演的并不是不可简约的元素，而是复合的结构，它们不能在理论物理学中扮演任何独立的角色。但我相信，在理论物理学发展的目前阶段中，这些概念仍然必须作为独立概念来使用；因为我们还远没有得到一种关于原子结构理论原理的可靠知识，使我们在理论上能由基本概念构成固体和时钟。

此外，有这样一种反对意见，认为自然界中没有真正的刚体，因此，所讲的刚体性质不能用到物理实在上去——这种反对意见绝不像乍看起来那么重要。因为要准确地测定量具的物理状态，使它对于别的量具来说，它的性状足以毫无歧义地允许它去代替“刚”体，那并不是困难的事。而这种量具，正是那些关于刚体的陈述所必须参照的。

整个实际几何是以一条为经验所能及的原理为基础的，我们现在试来了解这条原理。假设在一个实际刚体上标出两个记号。我们叫这样一对记号为一个截段（tract）。我们设想两个实际刚体，每个上面都标出一个截段。如果一个截段的两个记号能同另一个截段的两个记号永远重合，那么我们说这两个截段是“彼此相等”的。我们现在假定：

如果两个截段在某时某地是相等的，那么不论在何时何地它们永远都是相等的。

不仅欧几里得的实际几何，就是它的最接近的推广，即黎曼的实际几何，及其伴随的广义相对论，也都以这一假定为基础。在证明这一假定的实验根据中，我想只讲一个。空虚空间里光的传播现象对每一段当地时间都定出一个截段，即相应的光的路程，反之亦然。由此可知，上述关于截段的假定必定也适用于相对论中时钟的时间间隔。因此可以作如下表述：如果两只理想的钟在任何时刻和任何地点（那时它们是相互紧靠在一起的）走得同样快慢，那么当它们再在一起比较时，不管是在什么地方和什么时刻，它们将永远走得同样快慢。如果这定律对于自然的钟不成立，那么对于许多分隔开的属于同一化学元素的原子来说，它们的本征频率就应当不会像经验所显示的那样严格一致。锐光谱线的存在，是上述实际几何原理的一个令人信服的实验证明。分析到最后，这就是我们所以能够意味深长地来谈论四维空间-时间连续区的黎曼度规的理由。

按照这里所主张的观点，这个连续区的结构究竟是欧几里得的，还是黎曼的，或者任何别的，那是一个必须由经验来回答的物理学本身的问题，而不是一个只根据方便与否来选择的约定的问题。如果所考查的空间-时间区域愈小，实际刚体的排列定律愈接近欧几里得几何体的定律，那么黎曼几何会是站得住脚的。

固然，所提出的这个几何学的物理解释，直接用到小于分子数量级的空间时是失败了。但是，即使在那些关于基本粒子组成的问题中，它还是有部分的意义。因为即使在描述组成物质的带电基本粒子这样一个问题上，仍然可以尝试赋予场的概念以物理意义，这些场概念原来是为描述比分子大得多的物体的几何性状而给以物理定义的。要求黎曼几何的基本原理在它们的物理定义的范围以外仍然有物理实在的意义，这种企图是否正确，那只有靠它试用后成功与否来判明。结果可能会是：这种外推并不见得比把温度概念外推到分子数量级的物体上去会更有根据。

把实际几何的概念推广到宇宙数量级的空间上去，表面上看来，问题较少。当然，它会遭到这样的反对意见：由固体杆组成的结构，当它的空间范围愈来愈大时，它离理想的刚性也就愈来愈远。但是，我认为这种反驳不大会有什么根本性的意义。因此，我认为宇宙在空间上是否有限这个问题，从实际几何的意义来看，是一个十分有意义的问题。我甚至并不认为，要天文学不久就回答这个问题竟然是不可能的。让我们回想一下广义相对论在这方面的说法。它提出两种可能性：

1．宇宙在空间上是无限的。这只有当宇宙中集中在星体里的物质的平均空间密度等于零时才可能，那就是说，只有当所考查的空间容积愈来愈大，星的总质量对于它们散布着的整个空间容积的比率无限地趋于零时，才有可能。

2．宇宙在空间上是有限的。如果宇宙空间里有重物质的平均密度不等于零，那就必然如此。平均密度愈小，宇宙的容积就愈大。

我不能不提一下，我们能够举出一个理论论证来支持有限宇宙这假说。广义相对论指出，一个既定物体的惯性随着它近旁的有重物质的增加而增大；因此，把一个物体的总惯性归结为它同宇宙中其他物体之间的相互作用，那似乎是很自然的，这正像从牛顿时代以来，重力也确已完全归结为物体之间的相互作用一样。从广义相对论的方程能够推出：把惯性完全归结为物体之间的相互作用——如E．马赫所要求的——这只有当宇宙在空间上是有限的才有可能。

许多物理学家和天文学家并不关心这种论证。分析到最后，唯有经验才能决定这两种可能性中究竟哪一种在自然界中是现实的。经验怎样能够提供答案呢？首先似乎可以从我们观察到的部分宇宙来测定物质的平均密度。这种希望是不能实现的。可见星体的分布是极其不规则的，我们没有理由可以冒昧地把宇宙中的星体物质的平均密度看作是等于（比如说）银河里的平均密度。总之，不管所考查的空间有多大，我们总不能相信在那个空间的外面就没有更多的星了。这样，要估计平均密度似乎是不可能的。

但有另一条道路，我觉得它是比较可行的，尽管它也有很大的困难。因为，如果我们探究那些为经验所能及的广义相对论的结论歧离牛顿理论结论的偏差时，我们首先发现到的一个偏差是出现在引力物质的近旁的，这已在水星的例子中得到了证实。但是如果宇宙在空间上是有限的，那就有第二个歧离牛顿理论的偏差，用牛顿理论的语言，它可以这样来表述：引力场好像不仅是由有重物质所产生，而且还由均匀分布在整个空间里的带负号的质量密度所产生。由于这个虚设的质量密度必然是极小的，它只有在非常广大的引力体系中才能觉察到。

假定我们已知银河里星的统计分布和质量，然后应用牛顿定律，我们能算出引力场以及这些星所必须具有的平均速度，这个速度使银河在它的各个星体的相互吸引下不会坍缩，而得以保持它实际的大小。如果星的实际速度——它们能被测出来——是小于计算出来的速度，我们就能证明：在远距离处的实际吸引力比牛顿定律所定的要小。从这样一个偏差就能间接地证明宇宙是有限的。甚至还可能估计出它的空间大小。

我们能够设想一个有限但无边界的三维宇宙吗？

通常的回答是“不能”，但这不是正确的答案。下面所说的是为了要证明这个问题的答案应当是“能”。我要指出我们能够毫无特殊困难地用想象的图像来说明有限宇宙的理论，经过一些实践，我们不久将会对这种图像习惯起来。

首先是关于认识论性质的考查。几何-物理理论本身不能直接描绘出来，因为它只是一组概念。但是这些概念能用来把各种各样实在的或者想象的感觉经验在头脑里联系起来。因此，使理论“形象化”，就意味着想起那些为理论给以系统排列的许多可感觉的经验。在当前的情况下，我们应当问我们自己，要怎样来表示固体相互排列（接触）的性状，才能同有限宇宙理论对应起来。对此，我所要说的，其实并没有什么新鲜的东西；但是向我提出的很多疑问，证明对这些事情有兴趣的人的好奇心还没有得到完全满足。因此，对于我将要讲到的那个早已为大家所熟悉的部分，内行的人能否原谅呢？

当我们说我们的空间是无限的，我们要表示的意思是什么？那不过是说我们可以一个挨着一个地安放任意个同样大小的物体而永远填不满空间。假设我们有很多个同样大小的立方盒。依照欧几里得几何，我们能把它们在彼此的上下、左右、前后堆放起来，以填满空间的一个任意大的部分；但这样的构造会永无止境；我们能够继续加上愈来愈多的方盒，而永远不会没有余地。这就是我们说空间是无限的意思。比较恰当的说法是：假定刚体的排列定律是按照欧几里得几何所规定的，那么，空间对于实际刚体来说是无限的。

另一个无限连续区的例子是平面。在一个平面上，我们可以放上许多张方卡片，使任何一张卡片的每一边同另外一张卡片的边接在一起。这种构造永无止境；我们总能继续放上卡片——只要它们的排列定律符合于欧几里得几何的平面图形的排列定律。因此，对于这些方卡片来说，这个平面是无限的。所以，我们说平面是二维的无限连续区，而空间则是三维的无限连续区。这里所指的维数的意义，我想可以假定是大家都知道了的。

现在我们举一个有限但无边界的二维连续区的例子。我们设想有一个大球的表面和一些大小相同的纸制小圆片。我们把其中一个纸片放在球面的任何地方。如果我们在球表面上任意移动这纸片，在这过程中我们就碰不到边界。所以我们说这球的表面是一个没有边界的连续区。同时，这球面又是一个有限的连续区。因为要是我们把所有纸片都贴在球上，使得各个纸片都不互相重叠，这球的表面最后会被贴满，而没有容纳另外纸片的余地。这正是意味着这球的表面对于这些纸片是有限的。再者，球面是一个二维的非欧几里得连续区，那就是说，这些刚性图形所依据的排列定律并不符合欧几里得平面的定律。这能用如下方法来证明。在一个纸片的周围用六个纸片围起来，在其中每一个的周围再用六个纸片围起来，这样继续下去。如果这个构造是作在平面上，我们就得到一个连绵不断的排列，在那里，每一个纸片，除了那些放在边上的，都同六个纸片相接触。在球面上，这种构造在起初似乎也有成功希望，纸片半径对球半径的比率愈小，这种希望似乎就愈大。但是当构造进行下去，愈来愈明显的是，要纸片照上述的方式不间断地排列下去，那是不可能的。可是依照欧几里得平面几何则应当是可能的。这样，那些不能离开这个球面，甚至也不能从球面上看出三维空间的人们，只要凭纸片来做实验，就会发现他们的二维“空间”不是欧几里得空间，而是球面空间。

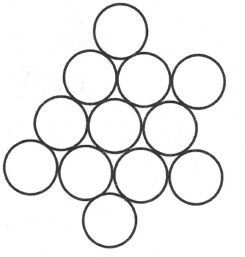
图1

从相对论的最近结果来看，很可能我们的三维空间也近似于球面空间，那就是说，在这空间里刚体的排列定律不是照欧几里得几何所规定的，而是近似地由球面几何所规定，只要我们所考查的那部分空间是足够大的话。到这里，读者的想象会犹豫起来。他会愤慨地叫喊：“没有谁能想象这种东西。”“可以这样说，但不能这样想。我能很好地想象一个球面，但是想不出它的三维类比。”

我们必须试图克服这种心理障碍，而有耐心的读者会明白这绝不是一项特别困难的事情。为了这个目的，我们首先要再来看一下二维球面几何。在附图中，设K是球面，它在S处同平面E相接触，为了便于表示，把这平面画成一个有边界的面。设L是球面上的一个圆纸片。现在让我们设想；在球面上同S径向相对的N点有一发光的点，它在平面E上投下纸片L的影L′。球上的每一点在平面上都有它的影。如果球K上的纸片移动了，平面E上的影L′也要移动。当纸片L是在S，它就几乎完全同它的影相叠合。如果它在球面上从S向上移动，平面上纸片的影L′也从S向外移动，并且愈来愈大。当纸片L接近发光点N时，这影就移向无穷远处，而变成无限大了。

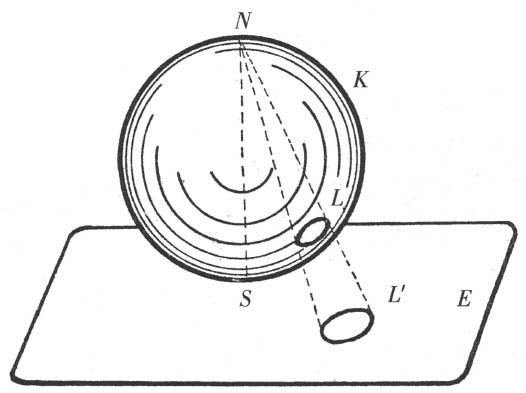
图2

现在我们提出这样的问题：在平面E上的纸片的影L′的排列定律是怎样的呢？显然它们是同球面上纸片L的排列定律完全一样。因为对于K上的每个图形，E上都有一个对应的投影图形。如果K上两个纸片相接触，它们在E上的影也相接触。平面上投影的几何同球面上纸片的几何是一致的。如果我们把这些投影叫做刚性图形，那么对于这些刚性图形，球面几何适用于平面E上。特别是，这平面对于纸片的影是有限的，因为在平面上只有有限个数的纸片的影能占到位置。

在这里，有人会说：“那是胡说。纸片的影不是刚性图形。我们只要拿一根尺在平面E上移动，就能使我们深信，当影在平面上从S移向无穷远处，影的大小就在不断增长。”但是，如果这根尺在平面上也像纸片的影L′一样地有伸缩，那又将怎样呢？那时就不可能使人看出这些影在离开S时会增长；这种断言因而不再有任何意义。事实上，关于纸片的影所能提出的唯一客观判断也正是这样：纸片的影的相互关系完全同欧几里得几何意义上的球面上的刚性纸片的关系一样。

我们必须留心记住，只要我们不能把纸片的影同那些能在平面E上运动的欧几里得刚体作比较，关于纸片影增大（当它们向无穷远处移动时）的陈述本身是没有客观意义的。对于影L′的排列定律来说，说S点是在平面上，同说它是在球面上，反正都一样。

上述球面几何在平面上的表示对我们是重要的，因为容易把它搬到三维的情况。

让我们设想我们空间里的一点S和很多个小球L′，所有这些小球都能彼此重合在一起。但这些球不是欧几里得几何意义上的刚性球；当它们从S向无穷远处运动时，它们的半径就在增长（从欧几里得几何的意义来说）；它的增长所遵循的定律同平面上那些纸片的影L′的半径增长定律一样。

在对我们这些L′球的几何性状在头脑里得到生动的映象以后，让我们假定在这种空间里根本不存在欧几里得几何意义上的刚体，而只有这种L′球性状的形体。那么，我们将得到一幅关于三维球面空间的清晰图像，或者说得恰当些，是一幅三维球面几何的图像。这里，我们的这些球必须叫做“刚性”，球。当它们离开S时，它们大小的增长不能由量杆的量度来检验出来，正像纸片的影在E平面上的情况一样，因为量度标准的性状同这些球的性状是一样的。空间是均匀的，就是说，在每一点的邻近，可以有同样的球的排列。⁽²⁾我们的这个空间是有限的，因为由于球“增大”的结果，只有有限个数的球能在空间里占到位置。

这样，以欧几里得几何给予我们的思维和想象的实践作为支柱，我们获得了球面几何的心理图像。通过特殊的想象构造，我们可以毫无困难地给这些观念以更大的深度和活力。用类似的方式，在所谓椭面几何的情况中也不会有困难。我今天唯一的目的是要指出，人的形象思维对于非欧几里得几何绝不注定是无能为力的。

————————————————————

(1) 这是爱因斯坦于1921年1月27日在普鲁士科学院所作的报告。讲稿最初发表在《普鲁士科学院会议报告》，1921年，第一部，123—130页，但删去了后面一小半；1921年柏林Springer出版的单印本《几何学和经验》（Geometrie und Erfahrung）则是全文。这里译自《思想和见解》232—246页。——编译者

(2) 如果我们再一次用球面上纸片的情况来说明，这是用不着计算就容易了解的——但只限于二维的情况。——原注