联合分布函数相互独立

先回忆一下，在第一章中，两随机事件A，B独立的定义：当时，称A，B相互独立。对于两个随机变量X，Y，有下面定义：

定义3.4.1对于任意两个实数集合，有

则称随机变量X，Y相互独立，简称X，Y独立。

利用概率的三条公理可知，当且仅当对任意实数x，y，有

即为时X，Y相互独立。　（3.4.2）

也就是说“对于任意的实数（x，y），（X，Y）的联合分布函数F（x，y）都等于X与Y的边际分布函数的乘积”可以作为变量x与Y独立的等价定义。

特别地，当（X，Y）为二元离散量时，设X，Y的可能取值为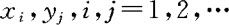，X与Y相互独立的定义等价于：对于任意的实数，都有

当（X，Y）为二元连续量时，由（3.4.2）式得，对于任意的实数x，y，有

由微积分知识知，两边积分处处相等，被积函数不一定要处处相等，即可以在面积为零的区域不相等。也就是说，被积函数除了面积为零的区域外处处相等，这种相等，我们称为几乎处处相等，即

几乎处处成立为连续量X，Y相互独立的等价定义。

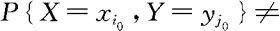
当（X，Y）为二元离散量时，由（3.4.3）知，若存在使得，则X与Y不独立；当（X，Y）为二元连续量时，若存在一个面积不为零的区域D0，使得，则X与Y亦不独立。

由（3.4.1）式可知，对任意集合时，X，Y独立的定义亦可写成

由独立的定义知，§3.1的例3.1.2中X与Y不独立。因为

也就是吸烟的多少与患呼吸道疾病是有关的，不独立的。

再如§3.3的例3.3.4中的X，Y亦不独立，因为当0＜x＜l时，。

特别地，若（X，Y）为二元正态量，由本章§3.3例3.3.5知，X与Y相互独立的充分必要条件为ρ＝0。因为当且仅当ρ＝0时，（3.4.4）式成立。

在实际问题中，当一个变量的取值不影响另一个变量取任何值的概率时，常认为这两个变量独立。

图3.4.1

例3.4.1　设在a地与B地间的距离（以公里计）为l（l＞1）的公路上有一辆急修车，急修车所在的位置是随机的。行使中的车辆抛锚地点也是随机的。求急修车与抛锚车的距离小于0.5公里的概率。

解　设急修车离A地的距离为X，抛锚车离A地的距离为Y。由题意知，x与y独立，且均在（0，l）上均勾分布。所要求的概率为

定理3.4.1　二元连续量X，Y相互独立的充要条件是X，Y的联合密度f（x，y）几乎处处可写成x的函数m（x）与y的函数n（y）的乘积，即

证明　先证必要性。当X，Y独立时，由（3.4.4）式知，下式几乎处处成立

记。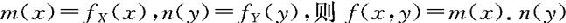

再证充分性。当时，由密度函数的性质知

记，那么ab＝1。再结合边际密度与联合密度函数的关系，可得

同理得，。所以

那么由（3.4.4）式知X，Y相互独立。

例3.4.2　问在下面两种情况下，X与Y独立吗？

（1）设（X，Y）的联合密度为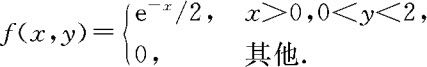

（2）设（X，Y）的联合密度为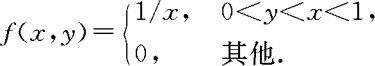

解　（1）记

故X，Y独立。

（2）由于f（x，y）不能分解成x的函数与y的函数的乘积，故X，Y不独立。从另一角度来看，我们可以求得X，Y的边际密度分别为

故当。那么由（3.4.4）知，也可知X，Y不独立。

以上关于二元随机变量的一些概念，容易推广到n元随机变量的情形。

例如：联合分布函数的概念，n元随机变量的联合分布函数为

其中为任意的实数。

关于边际分布函数，以下举例说明，其他情形可举一反三。例如：

当n＞2时，有的联合边际分布函数

类似地，也可以定义n元离散量与n元连续量。当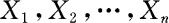的取值至多可列时，称为n元离散量；若对任意n维空间的集合D，存在非负函数，使得

成立，则称为n元的连续型随机变量，简称n元连续量，其中的称之为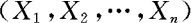的联合概率密度。

关于边际概率密度，类似地有，例如：

等等。

若对于任意的实数集，有

则称相互独立。

也即对任意的实数，有

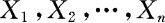则称相互独立。

当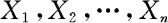为n元离散量时，亦有如（3.4.3）类似的独立的等价定义，当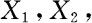为n元连续量时，亦有如（3.4.4）式相类似的独立的等价定义。

定义3.4.2　设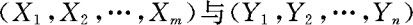分别为m元，n元的随机变量，分别用记它们的联合分布函数。再记的联合分布函数。

对任意的实数，若有

则称两向量组相互独立。

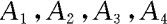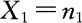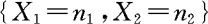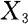例3.4.3　在n次独立重复的试验中，设每次试验有4个结果：。且每次试验发生的概率不变。设。再设在n次试验中发生的值；（2）在给定的条件下求的条件分布律；（3）在给定的条件下求的条件分布律。

解　（1）与n重贝努里试验及二项分布的讨论一样，可知事件

共有n!/（n1！n2！n3！n4！）种方式数。而每个Ai在确定的ni次发生的概率为，故有

（2）由题知

上面运算用到等式

所以。

故当n1＝0，1，…，n时，

（3）先求（X1，X2）的边际分布

那么当时，

即当给定的条件下，X3的条件分布为。

例3.4.4　一咨询台有A，B两个窗口，设每个顾客服务时间服从参数为λ的指数分布。有一天一开门，A窗口有一个人要求服务。B窗口有两人排队要求服务，设每人服务时间相互独立，求B窗口两人先于A窗口1人结束服务的概率。

解　设A窗口一人的服务时间为X1，B窗口的两个人的服务时间分别为X2，X3，由题意知，X1，X2，X3相互独立。所要求的概率即为

其中，的联合密度，由题意知，