回归分析原理

一、曲线拟合

将观测得到的变形结果拟合到一些曲线上，可以提供变形随时间变化的函数形式以及变形值与引起变形因素之间的函数关系，帮助确定变形的趋势，也可以利用所拟合的曲线对观测所得结果进行外推等趋势分析。

曲线拟合可以用以下基本方程来描述

式中，Yt为观测获得的变形值；εt为观测误差；f（t， θ）为描述所拟合曲线的函数，其中t及θ为已知及待定的参数。下面为一些典型的趋势模型：

（1）多项式趋势模型：Yt =a0 +a1t+a2t2 +…+antn；

（2）对数趋势模型：Yt=a + bln（t） ；

（3）幂函数趋势模型：Yt = atb ；

（4）指数趋势模型：Yt =aebt；

（5）双曲线趋势模型：Yt =a+b/t；

（6）修正指数模型：Yt=L-aebt。

二、线性回归分析原理

变形往往是由多方面的因素引起的。例如，高层建筑物的变形可能是建筑物本身的重量、日照、风荷载等作用产生的。而混凝±大坝的变形是由水库中水压力的作用、坝内温度的变化、建筑材料的徐变、基础地基的塑性变形等造成的。 目前，常用回归分析法来确定变形和变形原因之间的关系。

（一）一元线性回归进行变形测量资料分析

处理两个变量之间关系的回归分析称一元回归分析。当两个变量之间的关系为线性时，则称其为一元线性回归分析。当对变形量影响的因素很多时，还需用到多元回归分析。

大多数变形过程的曲线呈非线性分布，而许多非线性问题可以化成线性问题来解决，例如，当两个变量之间存在幂函数关系时，也即自变量x与因变量y之间的关系为：

对它取对数得：

若此时令y′=1gy， x′=lgx， b0′ =1gb0，则上式可以写成：

此式表示变量x′与y′之间的线性关系成立。也即通过变量变换，将非线性关系的变量转换成线性关系的变量。当因变量y与自变量x之间呈线性关系时，可用数学模型yi = b0 + bxi + vi来模拟观测数据。当观测数据多于两组时可用最小二乘法来计算参数b0、 b的估值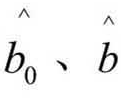为：

所求回归方程的有效性，可以通过检验相关系数ρ的显著性来实现。相关系数ρ的估值可用观测数据计算为：

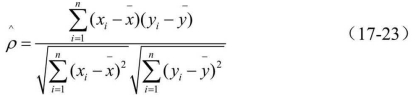
式中：

（二）多元线性回归进行变形测量资料分析

对于多个变量之间的关系，当它们之间存在非线性关系时，我们可以利用上述方法将它们转化成线性关系的变量。所以在处理多变量之间关系时，一般均可以将多元回归分析转化成多元线性回归分析。多元线性回归分析法是研究一个变量（因变量）与多个因子（自变量）之间的非确定关系（相关关系）的最基本的方法。该方法通过分析所观测的变形（效应量）和外因（原因）之间的相关性，来建立变形诱因与变形值之间关系的数学模型。其数学模型可表示为

式中，yt， xt1， xt2， …， xtp为t时刻变形量的观测值及影响该变形量的各因子取值，共有n组数据；p表示因子个数。具体分析步骤如下：

1.建立多元线性回归方程

多元线性回归数学模型如式（17-24）所示，可用矩阵表示为

y=xβ+ε （17-25）

式中，y为n维变形量的值（因变量），y= （y1， y2， …， yn） T； x是一个n× （p+1）的矩阵，它的元素是可以精确测量或可控制的观测量或它们的函数（自变量），其形式为

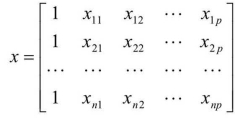
β是待估计参数向量（回归系数向量），β=（β0，β1，β2，…，βp）T；ε是服从正态分布N （0， σ2）的n维随机向量，ε=（ε1， ε2， …，εn） T。由最小二乘原理可求得β的估值为：

事实上，模型（17-24）只是对问题初步分析所得的一种假设，所以在求得多元线性回归方程后，还需要对其进行统计检验。

2.回归方程显著性检验

实际问题中，事先并不能判断因变量y与自变量x1， x2， …， xp之间是否有线性关系。在作线性回归分析之前，线性回归模型只是一种假设。在求得线性回归方程之后，还需要对回归方程进行统计检验，以确定原有的假设是否成立。如果因变量y与自变量x1， x2， …，xp之间不存在线性关系，则模型（17-24）中β为零向量，即有原假设H0: βi=0 （i=1， 2，…，p）。将此原假设作为模型（17-24）的约束条件，求得统计量

在原假设成立时，统计量F应服从F （p， n-p1-）分布，故在选择显著水平α后，可用下式检验原假设

对回归方程的有效性（显著性）进行检验。若式（17-28）成立，即认为对于显著水平α，y对x1， x2， …， xp有显著的线性关系，即回归方程是显著的。

（二）回归系数显著性检验

回归方程显著，并不意味着所有自变量x1， x2， … ， xp对因变量y的影响都显著。因此，有必要从回归方程中剔除那些可有可无的自变量，重新建立更为简单的线性回归方程。如果某个变量xj对y的作用不显著，则式（17-24）中该变量前面的系数βj就应该取为零。因此，检验因子xj是否显著的原假设应为H0∶βj=0。由式（17-24）可估算求得

式中，cjj为矩阵cx= （xTx） -1中主对角线上第j个元素。于是在原假设成立时，统计量符合故可组成检验原假设的统计量

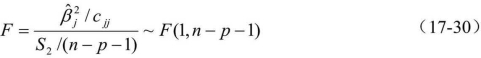
它在原假设成立时服从F （1， n-p-1）分布。上式的分子通常又称为因子xi的偏回归平方和。选择相应的显著水平α，可得分位值F1-α（1， n-p1-），若统计量|F|≥F1-α（1，n-p-1），则认为回归系数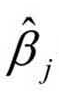在1-α的置信度下是显著的，否则是不显著的。

在进行回归因子显著性检验时，由于各因子之间的相关性，当从原回归方程中剔除一个变量时，其他变量的回归系数将会发生变化，有时甚至会引起符号的变化，因此对回归系数进行一次检验后，只能剔除其中的一个因子，然后重新建立新的回归方程，再对新的回归系数逐个进行检验，重复以上过程，直到余下的回归系数都显著为止。

三、逐步回归计算

逐步回归计算在F检验的基础上逐个接纳显著因子进入回归方程。当回归方程接纳一个因子后，由于因子之间的相关性，可使原先已在回归方程中的其他因子变得不显著，因而需要从回归方程中将其剔除。所以在接纳一个因子后，必须对已在回归方程中的所有因子的显著性进行F检验，剔除不显著的因子，直到没有不显著因子后，再对未选入回归方程的其他因子用F检验来确定是否接纳其进入回归方程。在此过程中，每次只接纳一个新的因子。反复运用F检验，进行剔除和接纳，直到得到所需的最佳回归方程。

逐步回归的计算方法可概括如下：

（1）由定性分析确定对因变量y的影响因子，设有q个。对每一个影响因子进行一元线性回归分析，计算其相应的残差平方和S2，然后选取与最小的S2相对应的因子作为第一个入选回归方程的因子。对该因子进行F检验，当其影响显著时，接纳该因子进入回归方程。

（2）再分别依次选取余下的q-1个因子的每一个，与上面已经选取的因子一起建立二元线性方程，计算它们的残差平方和及各因子的偏回归平方和，选择与max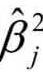（ /cjj）对应的因子为预选因子，做F检验，若影响显著，则接纳该因子进入回归方程。

（3）选取第三个因子，方法同（2），计算它们的残差平方和及各因子的偏回归平方和，同样，选择的因子为预选因子，作F检验，若影响显著，则接纳此因子进入回归方程。在选入第三个因子后，对原先已入选的回归方程的因子应重新进行显著性检验，在检验出不显著因子后，应将它剔除出回归方程，然后继续检验已入选的回归方程因子的显著性。

（4）在确认选入回归方程的因子均为显著因子后，则继续开始从未选入方程的因子中挑选显著因子进入回归方程，其方法与步骤（3）相同。反复运用F检验进行因子的剔除与接纳，直至得到所需的回归方程。

多元线性回归分析应用于变形测量数据分析主要包括以下两个方面：

（1）变形的成因分析，当式（17-24）中的自变量xt1， xt2， …， xtp为因变量的不同影响因子时，则该式可用来分析与解释变形与引起变形因子之间的因果关系。

（2）变形的预测预报，当式（17-24）中的自变量xt1 ， xt2 ， … ， xtp在某一时刻的值为已知或可观测时，则方程（17-25）可预测变形体在该时刻的变形。四、非线性回归分析原理

在一般情况下，类似于式（17-19），变形观测值y可表示为

式中， x为已知变量；y为变形量的观测值；ε为 y的随机误差；θ= （θ1， θ2…，θp） T为未知参数；f为模型函数，它的函数形式已知，但含有未知参数θ。如果f是θ的线性函数，则式（17-31）为前面叙述的线性回归模型，否则该式为非线性回归模型。

现在的问题是如何通过观测值y1， y2， … ， yn对模型及其参数进行统计回归分析。非线性回归模型的求解实际上是多个非线性参数的寻优问题， 目前还没有一种对各种情况都适用的通用方法。这里主要介绍计算非线性模型参数的高斯一牛顿法。

对于如式（17-31）的非线性模型，设有p个待估参数θ= （θ1， θ2…， θp），预先给定参数的初始值θ0，对模型函数在θ0处作一阶泰勒级数展开得

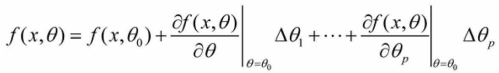
从而：

令li=yi-f （x，θ0）， Δθ=（Δθ1，Δθ2，…，Δθp），写成矩阵形式为

其中：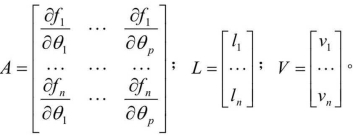

按最小二乘原理VTV=min可得

由于参数θ无任何先验信息，必须迭代求解。设第k步求得的参数解为kθ，则第k+1步计算步骤为： （1）对模型函数在kθ处按泰勒级数展开，重新线性化，组成如式（17-32）矩阵形式的观测方程式； （2）按最小二乘法解得第k+1步的参数解θ（k+1） = θk +Δ θ，若‖θ（k+1）-θk‖＜ε，迭代结束，否则重复上述步骤。

若残差不收敛或收敛速度很慢，可尝试使用麦夸脱法，此时最小二乘准则变为

参数解

式中，z为阻尼因子，一般取1～10之间的值。

高斯—牛顿法是一种线性逼近的方法，因此亦称为非线性最小二乘法。这种近似的可行性和对模型参数所作的推断的有效性决定于模型的非线性强度。当模型的非线性强度很强时，估计值对初始值的依赖性大，而且收敛速度慢，有时响应曲面可能多于一个极小值，这时不能保证收敛到正确的最小值；反之模型接近线性时，模型对初始值的依赖性不大，而且模型的收敛速度快。因此，应尽可能地寻找非线性强度弱的非线性模型。

从非线性模型的求解过程可以看出，即使假定εt是独立同分布且具有零均值和有限方差2σ的正态随机变量， 由于非线性回归模型的最小二乘估计量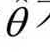不是yt的线性组合，因此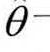一般也不服从正态分布，它亦不是θ的无偏估计和最小方差估计。然而当模型接近线性时，最小二乘估计量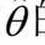的性质会接近于正态、无偏和最小方差性。

当矩阵ATA为病态时，方程组求解误差增大，甚至不收敛，这时可以考虑用零估计进行求解。