从事件无数次重复发生中导出的概率规律

在变量和那些被冠以偶然事件之名的未知原因之间，这些原因使得事件的发展处于不确定和不规则的状态中，但是，我们看到，随着对这些事件观测数目的增加，引人注目的规则性也就显示出来，这种规则性似乎是遵循着一种设计，这一直被当作是神圣设计的一种证明。但是，如果我们仔细思考这个问题，不久就会认识到这种规则性只是具有各自可能性的一些简单事件的自然过程而已，这些事件越是可能的，他们就应该越倾向于经常地发生。让我们想象一下，比如，一个包含白球和黑球的瓮，假设每次抽取一个球，把它放回后再进行下一次新的抽取。在最初几次抽取中，抽取到白球的数目与抽取到的黑球数目之比是最缺乏规则的；但是这种不规则性的变化不定的原因却对事件的规则进程轮番产生有利或不利的效果，在大量的抽取总和中它们彼此抵消，这就使得我们能够得到越来越好的瓮中所含有的白球和黑球之比的估计值，或者说越来越好地得到每次抽取一个白球或者一个黑球的各自可能性的估计值。从这些结果中可以导出以下定理：

抽取的白球数与抽取球的总数之比与瓮中所含有的白球与所有的球数之比的差不会超出一个给定的区间，这种情况的概率，无论这个区间有多小，会随着事件数目的增加而趋向于确定性（即概率为1）。

正如常识所表明的，这个定理难以用分析学证明。因此，杰出的几何学家雅克比·伯努利最先拥有这个定理的思想，他赋予他本人所给出的证明以极大的重要性。将生成函数的演算应用于这种情况，不仅给出关于这个定理的一个简单证明，而且更进一步，它给出了观察到的事件之比只是在一定的极限范围内不同于它们各自的可能性之比的概率。

从上述的定理中可以导出这样一个结果，可以将这个结果当作一个定律，即：当大量地考察自然的行为时，这些行为之比就非常接近于一个恒定的值。因此，尽管有年年岁岁的波动，但是，如果经过一个相当漫长的年岁，收成的总量实际上是相同的。所以，利用简便的预见，借用一个涵盖并不均匀分布的所有季节的收成这种方式，人就能够防止自己不受季节变化的影响。我并不期望从上面的定理中推出道德的原因。每年的出生数与总人口之比，以及结婚的人数与出生数之比却只有微小的变化；年出生数几乎是相同的，据说，在巴黎，邮局在一般的季节中因为写错或没有给出地址等原因而不能投寄的信的数目也几乎没有变化，人们在伦敦似乎也注意到了这种情况。

从这个定理中可进一步推出下面的结果：在一个无限延展的事件序列中，规则和恒定原因的影响从长远来看终究会压倒不规则原因的影响。正是这一点使得彩票的收益就像农业的收成一样确定，因为他们（发行方）本身所专享的机遇保证了他们在大量的投掷中具有总体上的优势。因此，大量的、有利的机遇既然总是伴随着一些建立和维持社会秩序的理性、正义和人性的永恒法则，那么遵从这些法则就会受益匪浅，而无视它们则危害极大。如果一个人借鉴一下历史和他本人的经历，那么，他就会看到所有的事实都会对这个演算的结果给予支持。试想一下，那些建立在人类的理性和自然权利之上的制度的幸福成果，在那些懂得如何去坚持和维护这些成果的民族中，再想一想，美好的信仰为那些将之作为其管理的基石的政府所带来的好处，这些政府由于一丝不苟地恪守他们的义务和承诺而付出了代价，为此他们是如何获得了补偿的！在国内具有多么大的感召力！在国外又具有何等的威望！相反，看一看那些由于其领导人的野心和背信弃义而陷入深渊的不幸民族吧！每一次由于对征服的贪婪而陷入狂热的强国渴望着统治世界，而在那些被威胁的国家中，对独立的渴望就（促使它们）形成一个联盟，而这个强国通常总是成为这个联盟的牺牲品。相似地，在那些导致各种国家的大小增加或者减少的变化无常的原因中，就像恒定的原因一样在起作用，自然的边界最终会被接受。那么，对于帝国的稳定和幸福两方面而言，重要的不是将这些边界扩展到由这些原因的作用而被不断地恢复到的边界之外——这就像由疾风暴雨所推高的海潮由于万有引力的作用再回落到其盆地。这是概率演算的另外一个结果，它得到了多起灾难性经历的验证。如果从恒定原因的影响这一着眼点来思考历史，它将给予人类最有益的经验教训的东西与由好奇心所引起的兴趣联系在一起。有时，我们会将必然发生的这些原因的结果归咎于发生其作用的偶然的环境。例如，当两个民族被一片浩瀚的海洋或者一段遥远的距离所隔离时，一个民族总是被另一个民族所统治就是违背事物的本性的。可以断定的是，从长远来看这个恒定的原因不断地与变化的原因交汇在一起，这些变化的原因以同样的方式起作用并且随着时间的进程而显示出来，也可以断定，它将以以下方式而告终：通过发现其自身足够强大到给予一个被征服民族以其天赋的独立性，或者将它与一个强大的邻国联合起来。

在大量的事例中，对风险的分析是最重要的，简单事件的可能性是未知的，我们被迫从过去的事件中去搜寻线索，这些线索能够在对于引发它们的原因的猜测中引导我们。上述的法则是关于由所观察的事件推出原因的概率的法则，在将生成函数的分析理论应用于这个法则时，就可以推出以下的定理：

当一个简单事件或者由几个简单事件组合而成的一个复合事件，比如像赌博游戏这样的事件，已被大量地重复多次，使观察的概率最大化的简单事件（的可能性），就是观察所显示出的最可能的东西，观察到的事件重复发生的次数越多，这个可能性就变得越大，如果重复的次数趋向于无穷，它就趋近于1。

在此可以发现两种近似值：一个是关于给出过去发生事件的最大概率的极限；另一个近似值是关于这些可能性落入这些极限之间的概率。如果这些极限是相同的，那么这个复合事件的重复发生会使得这个概率越来越大。如果这个概率保持相同，那么事件的重复发生会使得这些极限间的区间越来越窄。最终，这个区间变为零，这个概率变为确定性。

如果把这个定理应用于在欧洲的不同国家中观察男女婴出生数之比，就会发现在各个地区这个比都等于22比21，它表明更有可能生出男孩的事件具有极大的概率。进一步思考一下，在拿波里和圣彼得堡也有相同的情况，由此可见气候的作用没有影响。与一般流行的观念相反，我们猜想，男性出生的优势甚至在亚洲也存在。于是，我已邀请被派往埃及的法国学者着手调查这个有趣的问题，但是，很难获取精确的出生信息，这一点妨碍了他们对这个问题的解决。幸运的是，洪堡先生（M.de Humbold）在美洲以非凡的睿智、毅力和勇气观察和收集了无数新鲜的事物，其中他并没有忽视这个问题。他发现，在热带地区这个出生比与在巴黎观察到的比是相同的^[2]。这一点使我们认识到男性出生数较多是人类的一个一般规律。在我看来，不同种类的动物在这一点上所遵循的规律应当引起博物学家们的关注。

男婴出生数与女婴出生数之比与1相差无几，即使是在一个地区对出生进行大量的观察也是如此，这个事实在这方面向人们提供了一个与一般规律相反的结果，如果没有这个规律，人们或许就会得出结论说这个规律并不存在。为了得到这样一个结果，必须利用大量的数据并且要设法确保它以大概率被显示出来。例如，布丰（Buffon）在其《政治算术》中引用了勃艮第（Bourgogne）几个教区的例子，在这些地区，女婴的出生数超过了男婴，在这些教区中，在Carcelle-le-Grignon教区五年中有2 009个婴儿出生，其中1 026个女婴，983个男婴。尽管这些数据是相当大的，但是，它们却表明，更可能生女孩（的情况）只具有9/10的概率，并且这个概率小于在“猜正面-反面”游戏中连续四次没有掷出正面的可能性，它不足以确保探讨出这个反常的原因，如果在一个世纪的时间内追踪这个教区的出生情况，这个反常极有可能就不存在了^[3]。

为了确保公民的权利和义务，出生登记簿被极其细致地保存下来，这些登记簿可以有助于准确算出庞大帝国的人口而不必求助于对其居民的一一点数——一项费时费力的活动，并而难以做到精确。但是，为了达成这个目的，必须了解人口与年出生数之比。获得这个比的最精确的方法包括：一，在帝国境内选取一些尽可能同质的区域，目的是使得一般的结果不依赖于局部的环境。二，在给定的时间里，慎重细致地调查选中的每一个区域里的若干个教区的居民。三，从早于和晚于这个时间几年的出生数的记录中精确计算出对应于年出生数的平均数。这个数被居民总数所除即是年出生数与人口总数之比，这项调查计数的规模越大，这个比就越精确可靠。（法国）政府被这种人口调查的实效说服了，在我的请求下已经决定下令实施。从三十个地区均衡地扩展到整个法国，能够提供最精确信息的教区已经被挑选出来。他们调查的结果是：在1802年9月23日，居民的总数为2 037 615。在1800年，1801年和1802年，这些教区中的出生报表为：

那么，人口与年出生数之比为28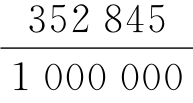，这个比大于原来所估计的数值。用这个比去乘法国的年出生数，我们就会得出国家的人口总数。然而，以这种方式求出人口数偏离真实的人口数不超过一个给定值的概率是多少？为了解决这个问题且将上述的数据应用于这个问题的解决，我发现，如果假设法国的年出生数为1 000 000，这个假设会导出28 352 845的总人口，几乎可以用300 000比1的赌注打赌：在这个结果中误差小于五十万。

从上述表中得出：男女婴出生数之比为22∶21，结婚数与出生数之比为3∶14。

在巴黎，受洗礼的男女婴数（之比）与22∶21这个比值相差无几。从1784年起，人们开始按不同性别进行登记，到1784年底，在首都（巴黎）有393 386个男婴和377 555个女婴受洗。这两个数的比几乎接近于25∶24。它显示出在巴黎有一个使得两性受洗人数趋于相等的特殊原因。如果将概率演算应用于这个问题，就会发现可以用238比1的赌去赌存在着这样一个原因，这一点足以促使人们值得去进行调查。经过再三的思考，我认为可以这样解释观察到的差异：那些农村和郊区的父母发现家中养儿子的好处，根据两性之间的出生比，相对于女婴，他们较少将男婴送到巴黎的孤儿院。这一点被这个孤儿院的登记表所证实。从1745年初至1809年底，这个孤儿院收纳了163 499名男孩和159 405名女孩。其中第一个数应该超过第二个数至少1/24，实际上，它只超过了1/38。这一点就证实了上述原因的存在，即如果忽略弃婴现象，在巴黎男女婴出生之比仍然是22∶21。

上述结果意味着，我们可以把出生比作为从一个包含无数个白球和黑球的瓮中抽球，这些球以这样一种方式混合：每个球被抽到的可能性是相等的。但是，不同年份的同样季节的差异可能会对男女婴年出生数之比产生影响，法国经度局^[4]在其《年鉴》中每年发表国家人口的变化表格。这些表格自1817年起已经开始出版：在那一年及其以后的五年，有2 962 361个男孩和2 781 997个女孩出生，男孩的出生数与女孩的出生数之比非常接近于16/15，每年的比与这个平均结果相差很小，最小的比是在1822年，只有17/16，最大的是在1817年，是15/14。这些比值相当不同于以上发现的比22/21。将概率的分析应用于这个差异，在将出生比作为从瓮中抽球的假设下，就会发现这是不可能的。因为，尽管这个假设似乎是一个不错的近似，但并非是严格精确的。在上面我们已经描述的出生数中有一些私生子——200 494名男孩和190 698名女孩。为此，男孩出生数与女孩出生数之比就是20/19，比平均比值16/15要小。这个结果与孤儿的出生情况具有相同的意义，它似乎证明了在非婚生子女集体中两性的出生数比婚生子女集体中两性的出生数更加接近于相等。从法国北部到南部气候的差异似乎并没有对男女婴的出生比产生可见的影响。在最南部的三十个地区给出的这个比为16/15，与全法国的比值相同。

自从出生数被记录以来，男性的出生数恒定地超过女性的出生数，在巴黎和伦敦都是如此，这种现象在某些学者看来是对神圣上帝的证明。他们认为，如果不是这样，由于不断干扰事件进程和谐的不规则原因的缘故，女婴的年出生数早应该有几次大于男婴的年出生数了。

然而，这个证明是（对上述分析）滥用的一个新例证，它经常被视为终极原因的组成部分，而在对问题进行深入考察中，当我们拥有需要的数据去解决它们时，这个原因就消失了。某些规则的原因导致了男性出生的优势，正在谈论的稳定性就是它的一个结果，并且当年出生数非常大时，这个规则原因的作用就压倒了由于偶然性而引起的反常的作用影响。对于这个稳定性将长期保持的概率的探讨属于从过去事件推断将来事件发生的概率分析的一个分支，它也是以下分析的基础：通过对从1745年至1784年观测的出生情况的讨论，几乎可以下一个4比1的赌注去赌：在一个世纪的时间内，在巴黎男孩的年出生数将会超过女孩的出生数，那么就没有理由对已经发生了半个世纪的这种状况感到惊讶不已。

让我们再给出另外一个例子，这个例子是随着观察事件的数量的增加而显示出比值的稳定性的增加。让我们想象把一系列瓮排成一个圈，其中每一个瓮中都有大量的白球和黑球，起初在这些瓮中白球与黑球的比是非常不同的，例如，一个瓮中可能仅有白球，而另一个瓮中可能仅有黑球。如果依次从第一个瓮中抽取一个球放入第二个瓮中，将第二个瓮的球搅拌均匀，再从第二个瓮中抽出一球放入第三个瓮中，这个过程持续下去，直到从最后一个瓮中抽取一球放入第一个瓮中。然后这个过程重复地一次一次进行下去。概率的分析向我们显示，在这些瓮中白球与黑球之比将以等同且等于白球的总数和与黑球的总数之比而结束。这样根据这个变化的规则图式，在这些比之间的初始的差别随着一连串的变化而消失，而让位于简单的秩序。现在，假设在原来的瓮之间放一个新瓮，并且新瓮中白球与黑球的总数与原来瓮中的黑球与白球总数不同。如果在混合的瓮中重复地一次一次进行我们刚才讨论的程序，那么在原来瓮中建立的简单秩序将被打破，且白球与黑球的比将从一个到另一个有相当的差异。但是这种差异将一点点消失，最终让位于新的秩序——瓮中白球与黑球有相同的比。这些结果或许可以推广到自然地正在发生的组合，其中，给元素以活力的永恒不变的力建立了行为的规则图式，从而揭示了隐藏在一片混沌迷雾中的、由令人敬畏的规律所统治的系统。

总之，那些似乎是依赖于偶然性的现象显现出不断地接近固定比的趋向。因此，如果我们设想一下，这些比中的每一个都包含在一个足够小的区间内，观察的平均值落入到这个区间的概率与确定性（1）的差最终将小于一个任意给定的量。所以，通过将之应用于大数次观察的概率演算，我们可以认识到这些比的存在。但是，为了不使自己迷失在徒劳的猜测中，在寻找这些原因之前，必须使自己确信它们以一个概率被表明是可能的，这个概率不会允许我们将其作为偶然性所导致的一些反常。生成函数的理论给出这个概率一个非常简单的式子。这个式子是由对下面两个量的乘积积分得到的：a）一个是一个量的微分，根据它从大数次的观测推断出不同于真值的结果；b）一个小于1的常量（依赖于问题的本质）并且使之作为一个幂的底数，其指数是那个差的平方与观察次数之比。在给定的区间内进行积分并被从负无穷到正无穷的相同的积分所除，这个积分将给出与真正的值的差位于这些区间的概率^[5]。这是基于大量的观察结果的概率的一般定律。