数学证明的种类

第二节　数学证明的种类

维特根斯坦承认，数学中有许多证明系统，从而也有许多种证明技巧。他说：“我要说，数学是各种各样的证明技巧的混合体——它的多种多样的应用和重要性即以此为基础。”（v.7，p.123，§46）为了说明数学证明技巧的多样性，他作了这样的设想：现今的某些，甚至全部数学证明系统已经与某个系统（比方说罗素的系统）相一致，因此所有的证明都可以在这个系统中进行，尽管是以曲折的方式进行。在这样的情况下，仍然可以把这个系统分解为许多个系统，其中一部分具有三角的性质，另一部分具有代数的性质，如此等等。这样就可以说，在这些不同的部分中会采用不同的证明技巧，因此数学证明系统不是只有一个，而是有许多个，数学就是一个由各种各样的证明技巧组成的混合体。

维特根斯坦认为，尽管数学证明系统有许多个，但可以把数学证明基本上分为两类：一类数学证明是在一个现存的公理系统的范围内进行的；另一类数学证明旨在建立一个新的公理系统。例如，在下述两种数学证明之间就存在着巨大差别：一是欧几里得几何学中的一个基本证明，即如果一个直角三角形abc（其两边长度为a和b，其斜边长度为c）所覆盖的面积为Z₂/4，那么这是一个等边三角形。另一是高斯（Gauss）的下述证明，即抛弃欧几里得的那个平行的假定并不会产生一个不连贯的几何系统，即使它的许多几何概念显然不同于欧几里得的几何概念。在欧几里得的证明系统中，学生采用什么样的特殊方法，这取决于他对欧几里得几何学中的基本概念的掌握，例如取决于他对毕达哥拉斯定理和等边三角形定义的掌握。相反，在高斯的证明系统中则没有那样一些强制因素在起作用。对于这两种数学证明的区别，维特根斯坦作了一个比喻：前一种只不过是做了一个“家庭作业”，后一种却是构造一个新的系统。

对于这两种数学证明的区别，维特根斯坦还举了下述事例加以说明。如果我知道初等三角学的规则，那我就能够检查sin2x=2sinx·cosx这个数学命题，而不能检查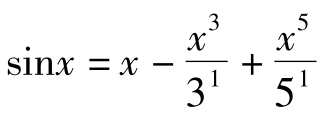……这个数学命题。他说：“这说明，初等三角学的正弦函数和高等三角学的正弦函数是不同的概念。”（v.4，pp.353-354，§25）这两个数学命题好像处于两个不同平面上，无论我怎样在第一个平面上移动，我都绝不可能达到更高平面上的数学命题。

维特根斯坦还认为，对于前一种数学证明需要注意的是，学生在做他的家庭作业时，不能随意改变欧几里得几何学的公理，而必须应用这个证明系统现有规则去作出证明，不要以为那些规则迫使我们以某种方式应用它们，也不要以为欧几里得几何学的规则迫使那个学生作出这个或那个证明。其实，当学生掌握了欧几里得几何学的规则时，不是这些规则迫使学生作出某个证明，而是我们教导学生以如此方式使用这些规则。换句话说，不是欧几里得几何学的规则迫使学生构造出这个或那个证明，而是教师教导学生以某种方式去使用这些规则。

对于“一个数学命题究竟只可能有一种证明还是可能有多种证明?”这样一个问题，也要从他关于上述两种证明的区别的观点加以考察。维特根斯坦并不反对这样的观点，即一个单一的数学命题可能在一个公理系统的范围内有许多种证明。不过，他坚决认为可以把一些对同一命题作出的证明翻译为另一种证明，在此限度内，它们是相同的证明。在他看来，只要概念之间的内在关系构成数学证明的本质，那么对于构造同一个数学命题，就不可能有两种不同的方法。例如，不能把欧几里得几何学中对一个人能够使用直尺和圆规去平分一条线的证明与对现代代数中的数学命题的证明相互对换，也不能把这两类数学命题看做是同义的。他说：“我们要记住，两个命题在相同的命题符号中相遇，这是不够的。因为我们怎么知道这个符号两次说的是相同的事?那必须由另外的关系而来。”（v.7，p.136，§62）他还认为，两个证明同一点的证明可以相互替换因而是同一个证明，这个论点不适用于下述这样的情况：比如，我从一个人的外衣挂在前厅和我听见他在吹口哨这两个事实中证明他此时在家里。在这个事例中，我们有两个相互独立的认识来源，这个证明所使用的是来自外部的理由，而数学证明应是对数学命题的分析。

与头一类证明相比，维特根斯坦更加关注第二类证明，即那种与构造新的公理系统相关的证明，也就是那种提出新概念的证明。他反复谈到，证明改变了我们的语法，改变了我们的概念。它产生了新的联系，创造了关于这些联系的新概念。他说：“证明创造了新概念这个想法大致可以表述为：证明不是在原有的基础上加上一些推理规则，而是建造了一座新的建筑物。证明是一个新的范型。”（v.7，p.120，§41）这就是说，证明所创造的新概念可以是比方说推理的新概念，正确推导的新概念。证明由于创造了新的符号，或者它本身就是一个新符号，从而创造了新概念，或者赋予作为其结果的命题以一个新的地位。他说：“当我说，一个证明引入了一个新概念，我的意思大致是这样的：对于语言的范型，证明提出了一个新的范型，就像有人调制了一种特别的紫色，从而确定了这种特定的颜色混合物，并给予它一个名称。”（v，7，p.115，§31）

维特根斯坦举出许多事例，以说明数学证明如何创造新概念。例如，某个人试图把一些部件拼合为某种图形。现在他看见一个模型，在这个模型中，那个图形的一部分显然完全是由他的部件拼合成的。这个模型就是一个证明，说明他原来的计划是行不通的。他说：“这个模型也像那个指明他能用那些部件做成图形的东西一样改变了他的概念，因为可以说，他在以前从来没有这样看待用这些部件拼合图形这个任务。”（v.7，p.176，§31）又如，如果我把“它将像这样”变成“它必须像这样”，那我便构造了一个新概念。这个概念包括了以前所没有的某种东西。当我说“如果这些推导是相同的，那就必定……”此时，我就把某种东西变成相等的标准，因此我改变了我的“相等”概念。又如，如果我首先引入“P∨Q”及“∽P”，用它们构成一些同语反复，然后作出（譬如说）序列∽P，∽∽P，∽∽∽P等等，并且引入诸如∽1P，∽2P……∽10P的记号。在这种情况下，“我要说，我们本来大概绝不会想到这种序列的可能性，而现在把一种新概念引入数的概念，尽管其方式相当简单和不恰当，但是这个例子向我说明了我需要的全部东西”（v.7，p.125，§46）。

维特根斯坦反复强调，数学证明给我指明一种新的联系，因此它也给我一个新的概念；数学创造了概念之间的联系，而一种新的概念联系也就是一个新概念；数学教会我用新的方法去操作概念，因此也可以说数学改变了我们使用概念的方式。例如，如果数学教导我们某个物体不是按照抛物线方程式移动着，那么数学也就教给我们一个新概念。他说：“显然，谁教会我们这个椭圆形等式，谁就教会我们一个新概念。可是，谁向我们证明这个椭圆形和这条直线在这些点上相切，谁也就在此时教给我们一个新概念。”（v.7，p.321，§44）