弗协调多主体认知逻辑系统(1)
郝旭东
本文将简述多主体认知逻辑的一些基本思想,然后在弗协调单主体认知逻辑的基础上,将弗协调逻辑的措施应用到有m(m≥1且m∈N)个主体认知逻辑中,从而建立一系列基本的弗协调多主体认知逻辑系统。
一、多主体认知逻辑思想简述
由于单主体认知逻辑不能满足科学快速发展的需要,于是多主体认知逻辑应运而生。多主体认知逻辑的命题,总是涉及两个以上的认知主体。我们把这种研究多个主体的认知命题形式及其规律的逻辑,称为多主体认知逻辑。在讨论多主体认知逻辑之前,有必要先来明确几个与“知道”的多样性相关的概念(2)。
在多主体逻辑中,主体之间相互知道是推理的重要依据,这也是主体将相互沟通的重要方式,我们把这种知道成为“互知”(Interaction Knowledge)。互知是指,一个认知主体不仅知道某一事态,而且知道他自己知道这一事态,以及知道其他认知主体也知道这一事态,并且其他主体也知道他们自己知道此事态。
在多主体认知逻辑推理中,有时各认知主体以他们都持有的知识为推理前提,我们称之为“共同知识”(Common Knowledge)。共同知识是指,一个命题是真并且一个群体的所有成员都知道该命题。共同知识总是相对于一定的群体来说的,并且总是有它自己的适用范围,我们称之为共同知识域。
与共同知识相关的是“公共知识”(Public Knowledge),它是经公共部门承认或某一群体约定的公共知识,群体的所有成员都有义务承认但并不一定为该群体每个成员实际上所确实知道的知识。
一个群体中每个主体分别持有的个别知识集中起来所推出的知识称为“协同知识”(Distributed Knowledge)。认知主体a知道A,而认知主体b知道A→C,那么尽管这两个认知主体都不是单独地知道C,但C仍是这个两人系统的协同知识。
多主体认知逻辑的语言主要是通过把认知主体的个体符从1扩展到m(m≥1,且m∈N),将单主体认知算子Ka和Pa分别扩展为认知算子K1,…,Km和P1,…,Pm(m≥1,且m∈N),并且增加多主体认知算子C(……为共同知识)、E(每个人都知道……)、D(……为协同知识)而得到的。由于算子C、E、D都可以通过算子K1,…,Km(m≥1,且m∈N)来定义得到,所以这些算子的语义赋值也可以通过算子K1,…,Km的语义赋值而得到。
多主体认知逻辑的常用公理模式有的形似单主体,有的则包含多主体认知算子C、E、D。简约起见,以下在讨论弗协调多主体认知逻辑系统公理模式的时候,将不涉及认知算子C、E、D。与这些公理模式相关的弗协调多主体认知逻辑系统,将作为今后的研究内容加以补充。
下面,就开始着手建立弗协调的多主体认知逻辑。
二、弗协调多主体认知逻辑
1.弗协调多主体认知逻辑的语言
弗协调多主体认知逻辑的语言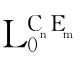 ,是由弗协调命题逻辑Cn(1≤n<ω)的语言L0通过附加多主体认知算子而得到的。
,是由弗协调命题逻辑Cn(1≤n<ω)的语言L0通过附加多主体认知算子而得到的。
弗协调多主体认知逻辑的初始符号如下:
(1)命题符:p1,…,pn,…,n为自然数;
(2)联结符: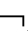 (否定),∧(合取),∨(析取),→(蕴涵);
(否定),∧(合取),∨(析取),→(蕴涵);
(3)认知符:K1,…,Km(认知),m∈N;
(4)标点符:)(右括号)和((左括号)。
其中,KiA的直观含义是“主体i认知A”,“认知”广义地代表“知道”、“相信”、“断定”等认知语词;PiA=df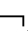 K
K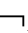
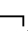 A(强的Ki,Pi可将定义中的
A(强的Ki,Pi可将定义中的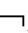 改为~),PiA的“主体i认为A是可能的”。
改为~),PiA的“主体i认为A是可能的”。
把由全体符形成的集合记作Expr(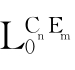 )。
)。
弗协调多主体认知逻辑的公式形成规则如下:
(1)单独的命题符是公式;
(2)若A是公式,则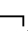 A是公式;
A是公式;
(3)若A和B都是公式,则(A∧B),(A∨B),(A→B)都是公式;
(4)若A是公式,i是认知个体变元,则KiA是公式;
(5)A是公式,当且仅当,A是有穷次引用以上四条规则而得到的。
全体命题符构成的集合记作Atom(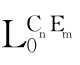 ),并称之为原子公式;全体公式构成的集合记作Form(
),并称之为原子公式;全体公式构成的集合记作Form(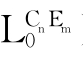 ),并且Atom(
),并且Atom(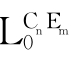 )≤Form
)≤Form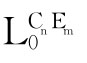 )。
)。
2.弗协调多主体认知逻辑的语义
定义2.1 框架
一个关于m个主体的框架是一个多元组F=(W,R1,…,Rm)。其中,W是认知可能世界或状态w的集合;对于i=1,…,m且m∈N,Ri是认知可能世界或状态W上的二元关系。
定义2.2 对于i=1,…,m且m∈N,
①如果A w E w′(wRiw′),则称Ri是持续的。
②如果A w(wRiw),则称Ri是自返的。
③如果A w1A w2A w3(w1Riw2∧w2Riw3→w1Riw3),则称Ri是传递的。
④如果A w1A w2A w3[w1Riw2∧w1Riw3→E w′∈W(w2Riw′∧w′Riw3)],则称Ri是弱有向的。
定义2.3 对于i=1,…,m且m∈N,
①一个框架是持续框架,iff,Ri是持续的。
②一个框架是自返框架,iff,Ri是自返的。
③一个框架是传递框架,iff,Ri是传递的。
④一个框架是弱有向框架,iff,Ri是弱有向的。
定义2.4 赋值
①V(A,w)=0→V(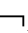 A,w)=1;
A,w)=1;
②V(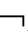
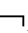 A,w)=1→V(A,w)=1;
A,w)=1→V(A,w)=1;
③V(B(n),w)=V(A→B,w)=V(A→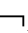 B,w)=1→V(A,w)=0;
B,w)=1→V(A,w)=0;
④V(A→B,w)=1→V(A,w)=0或V(B,w)=1;
⑤V(A∧B,w)=1→V(A,w)=1且V(B,w)=1;
⑥V(A∨B,w)=1→V(A,w)=1或V(B,w)=1;
⑦V(A(n),w)=V(B(n),w)=1→[(AΔ1B)(n),w]=[(Δ2A)(n),w]=1,其中,Δ1∈{∧,∨,→},Δ2∈{Ki},i=1,…,m且m∈N;
⑧V(KiA,w)=1→对于所有的i(i=1,…,m且m∈N),使得w′∈W[wRiw′→V(A,w′)=1]。
定义2.5 模型
一个关于m个认知主体的模型就是由一个框架F和F上的一个赋值V组成的二元组M=(F,V)。
①持续框架上的模型称为持续模型。
②自返框架上的模型称为自返模型。
③传递框架上的模型称为传递模型。
④弱有向框架上的模型称为弱有向模型。
定义2.6
设公式A∈Form(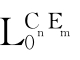 ),称A在模型M=(F,V)中为真,当且仅当,对任意的w∈W有V(A,w)=1,记作M
),称A在模型M=(F,V)中为真,当且仅当,对任意的w∈W有V(A,w)=1,记作M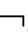 A;
A;
②称A在框架(W,R1,…,Rm)上有效,当且仅当,在框架(W,R1,…,Rm)上的任意赋值V都有M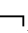 A,记作(W,R1,…,Rm)
A,记作(W,R1,…,Rm)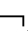 A或F
A或F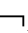 A;
A;
③令犉为任一框架类,称A在框架类上有效,当且仅当,对于任一F∈犉,A在F上有效,记作犉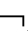 A;在由全体X-框架形成的类上有效的公式被称为X-有效的。
A;在由全体X-框架形成的类上有效的公式被称为X-有效的。
④令犕为一模型类,称A在模型类犕中为真,当且仅当,对于任一M∈犕,A在M中为真,记作犕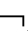 A。
A。
3.弗协调多主体认知逻辑诸系统
(1)弗协调多主体认知逻辑CnEmK(1≤n<ω)
弗协调多主体认知逻辑CnEmK(1≤n<ω)是在弗协调命题逻辑Cn(1≤n<ω)的基础上,通过增加公理A(n)→(KiA)(n)(i=1,…,m且m∈N)和多主体认知公理Ki(A→B)→(KiA→KiB)(i=1,…,m且m∈N)得到的。
CnEmK(1≤n<ω)的公理(模式)如下:
A1①A→(B );
);
②(A→B)→[A→(B→C)→(A→C)];
③A→(B ∧B);
∧B);
④A∧B ;
;
⑤A∧B→B;
⑥(A→C)→[(B→C)→(A∨B→C)];
⑦A ∨B;
∨B;
⑧B ∨B;
∨B;
⑨A∨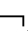 A;
A;
⑩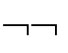 A
A ;
;
⑪B(n)→[(A→B)→((A→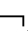 B)→
B)→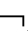 A)];
A)];
⑫A(n)∧B(n)→(A∧B)(n)∧(A∨B)(n)∧(A→B)(n);
A2①A(n)→(KiA)(n)(i=1,…,m且m∈N);
②Ki(A→B)→(KiA→KiB)(i=1,…,m且m∈N)。
CnEmK(1≤n<ω)的推理规则如下:
R1(分离规则)由A和A→B可推出B;
R2(认知概括规则)由A可推出KiA(i=1,…,m且m∈N)。
定义2.7 (形式)可推演关系和证明
称公式A在CnEmK(1≤n<ω)中是由Γ(形式)可推演的,记作Γ├CnEmKA,当且仅当,存在一个有穷的公式序列A1,A2,…,Am使得Am=A,并且对于任一的j(1≤j≤m),Aj满足下列条件之一:
①Aj是CnEmK(1≤n<ω)的公理之一;或者
②Aj∈Γ;或者
③存在小于j的l和k使得Aj是从Al和Ak(=Al j)利用R1得到;或者
j)利用R1得到;或者
④存在小于j的l使得Aj(=KiAl)是从Al利用R2得到的。
称公式A在CnEmK(1≤n<ω)中是可证的,记作├CnEmKA,当且仅当,存在一个有穷公式序列A1,A2,…,Am使得Am=A,并且对于任一的j(1≤j≤m),Aj满足下列条件之一:
①Aj是CnEmK(1≤n<ω)的公理之一;或者
②存在小于j的l和k使得Aj是从Al和Ak(=Al j)利用R1得到;或者
j)利用R1得到;或者
③存在小于j的l使得Aj(=KiAl)是从Al利用R2得到的。
在不引起混淆时,把Γ├CnEmKA简记为Γ├A;把├CnEmKA简记为├A。
由CnEmK(1≤n<ω)的公理(模式)和形成规则可知,系统Cn(1≤n<ω)是包含于CnEmK(1≤n<ω)的子系统。因此,Cn-定理也都是CnEmK-定理。
定义2.8 Cn-变形
设A是任意公式,A的Cn-变形记作A′,是删去A中所有模态算子和认知算子后得到的公式。严格地讲,Cn-变形是公式到公式的映射:
①(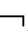 A)′=
A)′=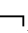 A′;
A′;
②(A∧B)′=A′∧B′;
③(A∨B)′=A′∨B′;
④(A→B)′=A′→B′;
⑤(KiA)′=A′,(i=1,…,m且m∈N)。
定理2.1 任一CnEmK-定理的Cn-变形都是Cn-定理。
证明:一个公式是CnEmK-定理,当且仅当,存在该公式的CnEmK-证明。施归纳于证明长度即可。
定理2.1也即是说,若A是CnEmK-定理,则A′是Cn-定理;若A′不是Cn-定理,则A不是CnEmK-定理。
定理2.2 在CnEmK(1≤n<ω)中有:
①若A∈Γ,则Γ├A;
②若Γ├A且Γ≤Δ,则Δ├A;
③若Δ├A且Δ├A→B,则Δ├B;
④若Γ├A且Δ,A├B,则Γ,Δ├B;
⑤若Γ1├A,Γ2├A→B,并且Γ1,Γ2≤Δ,则Δ├B。
定理2.3 在CnEmK(1≤n<ω)中有:
①若Γ1├A,Γ2├A→B,并且Γ1,Γ2≤Δ,则Δ├B。特别地,当Γ1=Φ时,有若├A,Γ2├A→B,并且Γ2≤Δ,则Γ2├B;当Γ2=Φ时,有若Γ1├A,├A→B,并且Γ1 Δ,则Γ1├B;
Δ,则Γ1├B;
②Γ├A1 2,Γ├A2
2,Γ├A2 3,…,Γ├Am-1
3,…,Γ├Am-1 m,→Γ├A1
m,→Γ├A1 m;
m;
③Γ├A∧B→Γ├A并且Γ├B;
④Γ├A→Γ├A∨B并且Γ├B∨A;
⑤Γ,A├C并且Γ,B├C→Γ,A∨B├C;
⑥Γ,A├B(n),且有Γ,A├B,Γ,A├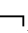 B→Γ├
B→Γ├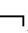 A。
A。
定理2.4 对于i=1,…,m且m∈N,在CnEmK(1≤n<ω)中有:
①├A→B→├KiA→KiB;├A→B→├PiA→PiB,(i=1,…,m且m∈N);
②├A→B→├KiA→KiB;├A→B→├PiA→PiB,(i=1,…,m且m∈N);
③├Pi~A→~KiA,(i=1,…,m且m∈N);
④├KiA∧KiB→Ki(A∧B),(i=1,…,m且m∈N);
⑤├PiA∨PiB→Pi(A∨B),(i=1,…,m且m∈N);
⑥├KiA∨KiB→Ki(A∨B),(i=1,…,m且m∈N);
⑦├Pi(A∧B)→PiA∧PiB,(i=1,…,m且m∈N);
定理2.5 对于i=1,…,m且m∈N,在CnEmK(1≤n<ω)中有:
①├A→├KiA;
②├A(n)→├(KiA)(n)。
证明:
①的证明:
因为├A,那么存在一个有穷公式序列A1,…,Am使得Am=A;并且对于任一的j(1≤j≤m),Aj满足下列条件之一:
a.Aj是CnEmK(1≤n<ω)的公理之一;或者
c.有小于j的l使得Aj是Al利用R2得到的。
对Am(=A)使用R2,可得KiA;因此,公式序列A1,…,Am,KiA就是├KiA的一个证明。
②的证明:
因为├A(n),那么存在一个有穷公式序列A1,…,Am使得Am=A(n);并且对于任一的j(1≤j≤m),Aj满足下列条件之一:
a.Aj是CnEmK(1≤n<ω)的公理之一;或者
b.有大于l和k的j使得Aj可以从Al和Ak(Ak=Al j)利用R1;或者
j)利用R1;或者
c.有小于j的l使得Aj是Al利用R2得到的。
由Am(=A(n)),根据公理A2①,使用R1,可得(KiA)(n);因此,公式序列A1,…,Am,(KiA)(n)就是├(KiA)(n)的一个证明。
定理2.6 对于i=1,…,m且m∈N,在CnEmK(1≤n<ω)中有:
①├K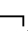
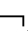 ~A→KiA;
~A→KiA;
②├A(n)→(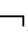 KiA→Pi~A);
KiA→Pi~A);
③├K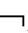
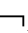 (A)(n)→KiA;
(A)(n)→KiA;
④├A(n)→(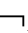 KiA→PiA(n));
KiA→PiA(n));
⑤├Ki(A∧B)→(KiA∧KiB);
⑥├KiA→~Pi~A;
⑦├Ki~A→~PiA;
⑧├~Pi(A∧B)→(~PiA∨~PiB);
⑨├Pi(A∨B)→(PiA∨PiB)。
推论2.1 对于i=1,…,m且m∈N,以下公式不是CnEK-定理:
①K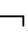
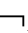 (A∧
(A∧ A) ②K
A) ②K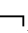
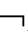 (A∧
(A∧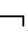 A)→KiB ③KiA∧K
A)→KiB ③KiA∧K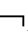
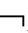 A→KiB
A→KiB
④P
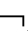 (A∧
(A∧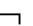 A)⑤P
A)⑤P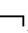
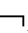 (A∧
(A∧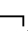 A)→PiB⑥PiA∧P
A)→PiB⑥PiA∧P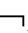
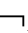 A→PiB
A→PiB
证明:对以上公式做Cn-变形,使用拟真值表即可以验证以上公式都不是C1-定理,因而它们也都不是Cn-定理,所以这些公式也就都不是CnEmK-定理。
定理2.7 CnEmK(1≤n<ω)公理(模式)A1①— 和A2①—②在任意框架上有效。
和A2①—②在任意框架上有效。
证明:首先,由定理2.1.12(3),可得公理(模式)A1①— 在任意框架上有效。下面验证公理A2①—②在任意框架上有效:
在任意框架上有效。下面验证公理A2①—②在任意框架上有效:
先验证公理A2①:A(n)→(KiA)(n),i=1,…,m且m∈N。
当V(A(n),w)=0时,根据赋值定义2.4⑧,可得V[(KiA)(n),w]=0;那么根据赋值定义2.4④,可得V[A(n)→(KiA)(n),w]=1。当V(A(n),w)=1时,根据赋值定义2.4⑧,可得V[(KiA)(n),w]=1;那么根据赋值定义2.4④,可得V[A(n)→(KiA)(n),w]=1。所以,由w的任意性,根据定义2.6,可得公理A2①A(n)→(KiA)(n)在任意框架上是有效的。
再验证公理A2②:Ki(A→B)→(KiA→KiB),i=1,…,m且m∈N。
当V(A,w)=0且V(B,w)=0时,根据赋值定义2.4④,可得V(A→B,w)=1;再根据赋值定义2.4⑧,可得V(KiA,w)=0且V(KiB,w)=0;因而,根据赋值定义2.4④,可得V(KiA→KiB,w)=1;那么再根据赋值定义2.4④,可得V[Ki(A→B)→(KiA→KiB),w]=1。同理可证,当V(A,w)=0且V(B,w)=1时,V(A,w)=1且V(B,w)=0时,V(A,w)=1且V(B,w)=1时,都有V[Ki(A→B)→(KiA→KiB),w]=1。所以,由w的任意性,根据定义2.6,可得公理A2②Ki(A→B)→(KiA→KiB)在任意框架上是有效的。
定理2.8 对于i=1,…,m且m∈N,令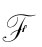 是一个框架类,则有:
是一个框架类,则有:
①若A,A→B在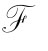 上有效,则B在
上有效,则B在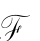 上有效。
上有效。
②若A在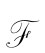 上有效,则KiA在
上有效,则KiA在 上有效。
上有效。
①的证明:
②的证明:
设A在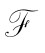 上有效,令(W,R1,…,Rm)是
上有效,令(W,R1,…,Rm)是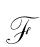 中的任一框架,V是该框架上的任一赋值。那么,对于任意一个w∈W,有V(A,w=1)。因此,对任一个w′∈W,有wRiw′→V(A,w′)=1。因此就有对于i=1,…,m,V(KiA,w)=1;由w的任意性可得(W,R1,…,Rm)
中的任一框架,V是该框架上的任一赋值。那么,对于任意一个w∈W,有V(A,w=1)。因此,对任一个w′∈W,有wRiw′→V(A,w′)=1。因此就有对于i=1,…,m,V(KiA,w)=1;由w的任意性可得(W,R1,…,Rm)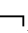 KiA,再由(W,R1,…,Rm)的任意性可得,对于i=1,…,m有
KiA,再由(W,R1,…,Rm)的任意性可得,对于i=1,…,m有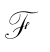
 KiA,即,对于i=1,…,m且m∈N,KiA在
KiA,即,对于i=1,…,m且m∈N,KiA在 上有效。
上有效。
定理2.9 CnEmK(1≤n<ω)是可靠的,即:
①若Γ├CnEmKA,则Γ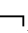 CnEmKA;②若├CnEmKA,则
CnEmKA;②若├CnEmKA,则 CnEmKA。
CnEmKA。
证明:由于②是①当Γ=Φ的特例,所以,仅证明①即可。由定理2.7和定理2.8,施归纳于证明长度可得。
定义2.9
①对任意公式集Γ≤Form(LCnEm0),Γ*={A∈Form(LCnEm0):Γ├A},若Γ*=Γ,则称Γ演绎封闭的。
②称Γ为不足道的,当且仅当,Γ*=Form(LCnEm0);否则,称之为足道的。
③称一足道集Γ是极大的,当且仅当,对任意公式A,若A∈Γ,则Γ∪{A}是不足道的。
④称Γ是不协调的,当且仅当,有公式A使得Γ├A且Γ├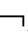 A。
A。
引理2.1 令Γ≤Form(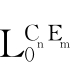 )且A∈Form(
)且A∈Form(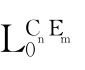 ),那么,
),那么,
①如果有Γ├A∧~A,那么有Γ是不足道的;
②如果Γ是不足道的,那么存在公式A使得Γ├A∧~A;
③Γ├A,当且仅当,Γ∪{~A}是不足道的;
④如果Γ是极大足道的且A∈Γ,那么Γ∪{A}├A∧~A;
⑤如果Γ是极大足道的且A∈Γ,那么Γ∪{A}├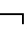 A。
A。
引理2.2 如果Γ是极大足道的,那么:
①Γ├A,当且仅当,A∈Γ;
②若A∈Γ,则~A∈Γ;若~A∈Γ,则A∈Γ;
③A∈Γ或~A∈Γ;
④若├A,则A∈Γ;
⑤若A,A(n)∈Γ,则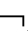 A∈Γ;若
A∈Γ;若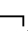 A,A(n)∈Γ,则A∈Γ;
A,A(n)∈Γ,则A∈Γ;
⑥若A∈Γ,A→B∈Γ,则B∈Γ;
⑦若A(n)∈Γ,则A∈Γ或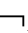 A∈Γ;
A∈Γ;
⑧若A(n)∈Γ,则(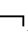 A)(n)∈Γ。
A)(n)∈Γ。
引理2.3 如果Γ是极大足道的,那么:
①A∈Γ→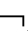 A∈Γ;
A∈Γ;
②
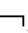 A∈Γ→
A∈Γ→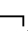 A∈Γ;
A∈Γ;
④A→B∈Γ ∈Γ或B∈Γ;
∈Γ或B∈Γ;
⑤A∧B∈Γ ∈Γ且B∈Γ;
∈Γ且B∈Γ;
⑥A∨B∈Γ ∈Γ或B∈Γ;
∈Γ或B∈Γ;
⑦A(n),B(n)∈Γ→(A→B)(n),(A∧B)(n),(A∨B)(n),(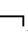 A)(n),(KiA)(n)∈Γ。
A)(n),(KiA)(n)∈Γ。
引理2.4 (极大扩张引理) 每一个足道集都可以扩张成极大足道集。
引理2.5 Γ├A,当且仅当,A是maxΓ中任一极大足道集的元素,即,A X∈maxΓ(A∈X),也即,├A 是任一个极大足道集的元素。
是任一个极大足道集的元素。
定义2.10 CnEmK(1≤n<ω)的典范模型是M*=(W*,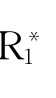 ,…,
,…, ,
,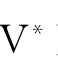 ),其中
),其中
W*=max;
X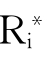 Y→{A∈Form
Y→{A∈Form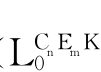 ):KiA∈X}≤Y;
):KiA∈X}≤Y;
![]()
引理2.6 对每一个非负整数k,有:
①XR*iY→{A∈Form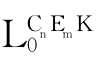 ):KiA∈X}≤Y;
):KiA∈X}≤Y;
②XR*iY→{PiA∈Form(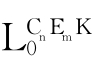 ):A∈Y}≤X。
):A∈Y}≤X。
证明:施归纳于k可证。
引理2.7 F*=(W*,R*1,…,R*m)是一个CnEmK-框架。
证明:该定义即是要证明任意框架都是CnEmK-框架。首先,分离规则和认知概括规则在任意框架上都是有效的;其次,Cn公理在任意框架上也都是有效的;再次,由定理2.7可得,对于i=1,…,m且m∈N,公理A2①A(n)→(KiA)(n)和公理A2②Ki(A→B)→(KiA→KiB)是在任一框架上是有效的。因此,任意框架都是CnEmK-框架。所以,F*=(W*,R*1,…,R*m)也是一个CnEmK-框架。
引理2.8 M*=(W*,R*1,…,R*m,V*)是一个CnEmK-模型。
证明:由引理2.7可知,F*=(W*,R*)是一个CnEK-框架。引理2.3保证V*满足赋值定义2.4的①—⑦。下面验证对于i=1,…,m,V*满足赋值定义2.4的⑧。首先,我们有:
V*(KiA,X)=1
→KiA∈X
(V*的定义)
 X′∈W*(XR*iX′
X′∈W*(XR*iX′ ∈X′)(R*i的定义)
∈X′)(R*i的定义)
 X′∈W*[XR*iX′→V*(A,X′)=1](V*的定义)
X′∈W*[XR*iX′→V*(A,X′)=1](V*的定义)
其次,假设A X′∈W*[XR*iX′→V*(A,X′)=1],根据V*的定义则有:
A X′∈W*(XR*iX′ ∈X′)
∈X′)
→{B:KiA∈X}├A(引理2.5)
→X中有KiB1,…,KiBk,使得
├B1∧…∧Bk (形式可推演定义)
(形式可推演定义)
→X中有KiB1,…,KiBk,使得
├KiB1∧…∧KiBk→KiA(定理2.4①)
已知KiB1,…,KiBk∈X,根据引理4.2.3(3)则有
KiB1∧…∧KiBk∈X
→KiA∈X(引理2.2⑥)
→V*(KiA,X)=1(V*的定义)
因此,V*满足赋值定义2.4的⑧。所以,M*=(W*,R*,V*)是一个CnEmK-模型。
定理2.10 CnEmK是完全的,即:
①如果Γ├CnEmKA,那么Γ CnEmKA;②如果├CnEmKA,那么
CnEmKA;②如果├CnEmKA,那么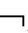 CnEmKA。
CnEmKA。
证明:若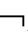 CnEmKA,
CnEmKA,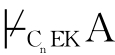 设。根据极大扩张引理,则存在一个极大足道集w且A∈w;由于w∈W*,所以V*(A,w)=0;又因为(W*,
设。根据极大扩张引理,则存在一个极大足道集w且A∈w;由于w∈W*,所以V*(A,w)=0;又因为(W*,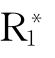 ,…,
,…, )是CnEmK-框架,所以(W*,
)是CnEmK-框架,所以(W*,
R1*,…,Rm*)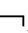
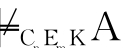 nm。这与前提不符,因此,假设错误。所以,若
nm。这与前提不符,因此,假设错误。所以,若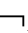 CnEmKA,则├CnEmKA。
CnEmKA,则├CnEmKA。
(2)弗协调多主体认知逻辑CnEmD(1≤n<ω)
CnEmD(1≤n<ω)是在CnEmK(1≤n<ω)的基础上,通过增加多主体认知公理KiA→PiA(i=1,…,m且m∈N)得到的。
CnEmD(1≤n<ω)的公理(模式)如下:
①CnEmK(1≤n<ω)的全部公理(模式);
②A3 KiA→PiA(i=1,…,m且m∈N)。
CnEmD(1≤n<ω)的推理规则如下:
R1(分离规则)由A和A→B可推出B;
R2(认知概括规则)由A可推出KiA(i=1,…,m且m∈N)。
由以上CnEmD(1≤n<ω)的公理(模式)和推理规则可知,系统CnEmD(1≤n<ω)是系统CnEmK(1≤n<ω)的直接扩张。因而,CnEmK-定理也都是CnEmD-定理。
定理2.11 CnEmD(1≤n<ω)是可靠的,即:
①若Γ├CnEmDA,则Γ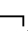 CnEmDA;②若├CnEmDA,则
CnEmDA;②若├CnEmDA,则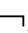 CnEmDA。
CnEmDA。
证明:类似于定理4.2.9的证明,略。
引理2.9 F*=(W*,R*1,…,R*m)是一个CnEmD-框架。
证明:证F*是一个CnEmD-框架,也即是要证F*是一个持续框架,只需证F*满足:A X(X∈W*)→E X′(XR*iX′),这等价于需证:A X(X∈W*)→E X′({A:KiA∈X}≤X′)。
如果{A:KiA∈X}是足道的,那么根据极大足道集扩张引理,它总是可以扩张为一个极大足道集。设该极大足道集为Γ,Γ属于极大足道集的集合max(即∈W*),并且足道集{A:KiA∈X}又总是属于Γ,所以就可以将Γ视为X′。因此,只需证明{A:KiA∈X}是足道的。
下面,证明{A:KiA∈X}是足道的。
给定前提X∈W*和公式集{A:KiA∈X},假设{A:KiA∈X}是不足道的,则
{A:KiA∈X}中有公式集{B1,…,Bm}
使得B1∧…∧Bm├C∧~C (引理2.1①)
→B1∧…∧Bm├C且B1∧…∧Bm├~C (定理2.3③)
→├B1∧…∧Bm→C且├B1∧…∧Bm→~C (演绎定理)
→├KiB1∧…∧KiBm→KiC且├KiB1∧…∧KiBm→Ki~C (定理2.4①)
再由前提{KiB1,…,KiBm}∈X,根据定理4.2.3(3),则有
KiB1∧…∧KiBm∈X
→KiC∈X且Ki~C∈X (引理2.2⑥)
→Pi~C∈X (公理A3和引理2.2⑥)
→~KiC∈X (定理2.4③)
因为X中同时有公式KiC和公式~KiC,根据引理2.1①可得,X是不足道的,即X∈W*,而X∈W*是给定的前提。因此,假设错误。于是,{A:KiA∈X}是足道的。所以,F*是一个持续框架,即,F*=(W*,R*1,…,R*m)是一个CnEmD-框架。
引理2.10 M*=(W*,R*1,…,R*m,V*)是一个CnEmD-模型。
证明:由引理2.9可知,F*=(W*,R*)是一个CnEmD-框架;又由引理2.8可知V*满足赋值定义2.4的①—⑧。所以,M*是一个CnEmD-模型。
定理2.12 CnEmD(1≤n<ω)是完全的,即:
①如果Γ├CnEmDA,那么Γ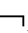 CnEmDA;②如果├CnEmDA,那么
CnEmDA;②如果├CnEmDA,那么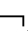 CnEmDA。
CnEmDA。
证明:若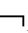 CnEmDA,
CnEmDA,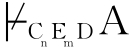 设。那么,根据极大扩张引理,则存在一个极大足道集w且A∈w;由于w∈W*,所以V*(A,w)=0;又因为(W*,R*)是CnEmD-框架,所以
设。那么,根据极大扩张引理,则存在一个极大足道集w且A∈w;由于w∈W*,所以V*(A,w)=0;又因为(W*,R*)是CnEmD-框架,所以
(W*,R*) 。因此,假设错误。所以,若
。因此,假设错误。所以,若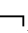 CnEmDA,则├CnEmDA。
CnEmDA,则├CnEmDA。
定理2.13 公理A3不是CnEmK-定理。
证明:我们构造一个具体的模型(W,R1,…,Rm,V)使用反模型的方法,来证明它是CnEK-模型,并且它是公理A3的反模型。
设(W,R1,…,Rm,V)是一个多元组,其中W是认知可能世界集,Ri空集,V是任一赋值。由模型定义可知,(W,Ri,V)是一个模型。根据CnEmK-引理2.6可知,任一模型也都是CnEmK-模型,所以此模型也是CnEmK-模型。下面证明它又是KiA→PiA(i=1,…,m且m∈N)的反模型。
由R空集可知,不存在w′∈W使得wRiw′,根据赋值定义2.4⑧则有,对任一V都有V(KiA,w)=1。有根据Pi定义和赋值定义2.4⑧可知,PiA在w上总是为假,即,对任一V都有V(PiA,w)=0。因此,对任意的V有V(KiA→PiA,w)=0。所以,公理A3在该模上非有效。所以,公理A3也不是CnEmK的定理。
定理2.14 系统CnEmD(1≤n<ω)是CnEmK(1≤n<ω)的真扩张。
证明:由定理2.13和真扩张的定义可得。
(3)弗协调多主体认知逻辑CnEmT(1≤n<ω)
CnEmT(1≤n<ω)的公理(模式)如下:
①CnEmK(1≤n<ω)的全部公理(模式);
②A4 KiA (i=1,…,m且m∈N)。
(i=1,…,m且m∈N)。
CnEmT(1≤n<ω)的推理规则如下:
R1(分离规则)由A和A→B可推出B;
R2(认知概括规则)由A可推出KiA(i=1,…,m且m∈N)。
由以上CnEmT(1≤n<ω)的公理(模式)和推理规则可知,系统CnEmT(1≤n<ω)是系统CnEmD(1≤n<ω)的直接扩张。因而,CnEmK-定理和CnEmD-定理也都是CnEmT-定理。
定理2.15 CnEmT(1≤n<ω)是可靠的,即:
①若Γ├CnEmTA,则Γ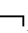 CnEmTA;②若├CnEmTA,则
CnEmTA;②若├CnEmTA,则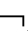 CnEmTA。
CnEmTA。
证明:类似于定理2.9的证明,略。
引理2.11 F*=(W*,R*1,…,R*m)是一个CnEmT-框架。
证明:证F*是一个CnEmT-框架,也即是要证F*是一个自返框架,只需证F*满足:A X∈W*(XR*iX),这等价于需证:A X∈W*({A:KiA∈X}≤X)。
给定前提X∈W*和公式集{A:KiA∈X},设任意公式B∈{A:KiA∈X},根据定理2.2①,可得{A:KiA∈X}├B;再根据定理2.5①,可得{A:KiA∈X}├KiB,于是可得KiB∈X;由公理A4,可得├KiB→B;所以根据引理2.2⑥,可得B∈X;因为B的任意性,因此{A:KiA∈X}≤X。所以,F*是一个自返框架,即,F*=(W*,R*1,…,R*m)是一个CnEmT-框架。
引理2.12 M*=(W*,R*1,…,R*m,V*)是一个CnEmT-模型。
证明:由引理2.11可知,F*=(W*,R*)是一个CnEmT-框架;又由引理2.8可知V*满足赋值定义2.4的①—⑧。所以,M*是一个CnEmT-模型。
定理2.16 CnEmT是完全的,即:
①如果Γ├CnEmTA,那么Γ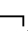 CnEmTA;②如果├CnEmTA,那么
CnEmTA;②如果├CnEmTA,那么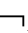 CnEmTA。
CnEmTA。
证明:设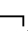 CnEmTA,也即,A是CnEmT有效的,则有
CnEmTA,也即,A是CnEmT有效的,则有
 在任意一个CnEmT-框架上有效 (框架类有效定义)
在任意一个CnEmT-框架上有效 (框架类有效定义)
 在任意一个CnEmT-模型上有效 (模型类为真定义)
在任意一个CnEmT-模型上有效 (模型类为真定义)
 在M*中为真 (M*是CnEmT-模型)
在M*中为真 (M*是CnEmT-模型)
 X∈max[V*(A,X)=1] (模型为真定义)
X∈max[V*(A,X)=1] (模型为真定义)
 X∈max(A∈X) (V*的定义)
X∈max(A∈X) (V*的定义)
→├CnEmTA (引理2.5)
定理2.17 公理A4不是CnEmK-定理。
证明:类似于定理2.13的证明,只需构造一个具体的模型(W,R1,…,Rm,V)使用反模型的方法,就可以证明它是CnEmD-模型,并且它是公理A4的反模型。
定理2.18 系统CnEmT(1≤n<ω)是CnEmK(1≤n<ω)的真扩张。
证明:由定理4.2.17和真扩张的定义可得。
(4)弗协调多主体认知逻辑CnEm4(1≤n<ω)
CnEm4(1≤n<ω)是在CnEmT(1≤n<ω)的基础上,通过增加多主体认知公理(A5)KiA→KiKiA(i=1,…,m且m∈N)而得到的。
CnEm4(1≤n<ω)的公理(模式)如下:
①CnEmT(1≤n<ω)的全部公理(模式);
②A5 KiA→KiKiA(i=1,…,m且m∈N)。
CnEm4(1≤n<ω)的推理规则如下:
R1(分离规则)由A和A→B可推出├B;
R2(认知概括规则)由A可推出KiA(i=1,…,m且m∈N)。
由以上CnEmT(1≤n<ω)的公理(模式)和推理规则可知,系统CnEm4(1≤n<ω)是系统CnEmT(1≤n<ω)的直接扩张。因而,CnEmK-定理和CnEmT-定理也都是CnEm4-定理。
定理2.19 CnEm4(1≤n<ω)是可靠的,即:
①若Γ├CnEm4A,则Γ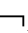 CnEm4A;②若├CnEm4A,则
CnEm4A;②若├CnEm4A,则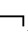 CnEm4A。
CnEm4A。
证明:类似于定理2.9的证明,略。
引理2.13 F*=(W*,R*1,…,R*m)是一个CnEm4-框架。
证明:证F*是一个CnEm4-框架,也就是证明F*是一个传递框架,只需证F*满足:A X1A X2A X3∈W*(X1R*iX2∧X2R*iX3→X1R*iX3)。这等价于需证:对于A X1A X2A X3∈W*,有:({A:KiA∈X1}≤X2)且({A:KiA∈X2}≤X3)→({A:KiA∈X1}≤X3)。
给定前提A X1A X2A X3∈W*及({A:KiA∈X1}≤X2)且({A:KiA∈X2}≤X3),设任意公式KiA∈X1,根据公理A5,可得├KiA→KiKiA;那么根据引理2.2⑥,可得KiKiA∈X1;由X1R*iX2,可得KiA∈X2;再由X2R*iX3,可得KiA∈X3;因此,A X1A X2A X3∈W*(X1R*iX2∧X2R*iX3→X1R*iX3),所以,F*是一个传递框架,即,F*是一个CnEm4-框架。
引理2.14 M*=(W*,R*1,…,R*m,V*)是一个CnEm4-模型。
证明:由引理2.13可知,F*=(W*,R*)是一个CnEm4-框架;又由引理2.8可知
V*满足赋值定义2.4的①—⑧。所以,M*是一个CnEm4-模型。
定理2.20 CnEm4(1≤n<ω)是完全的,即:
①如果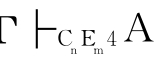 ,那么
,那么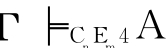 ;②如果├CnEm4A,那么
;②如果├CnEm4A,那么 CnEm4A。
CnEm4A。
证明:若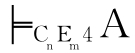 ,设
,设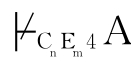 。那么,根据极大扩张引理,则存在一个极大足道集w且A∈w;由于w∈W*,所以V*(A,w)=0;又因为(W*,R*)是CnEm4-框架,所以(W*,
。那么,根据极大扩张引理,则存在一个极大足道集w且A∈w;由于w∈W*,所以V*(A,w)=0;又因为(W*,R*)是CnEm4-框架,所以(W*,
R*)├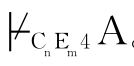 。因此,假设错误。所以,若
。因此,假设错误。所以,若 CnEm4A,则├CnEm4A。
CnEm4A,则├CnEm4A。
定理2.21 公理A5不是CnEm4-定理。
证明:类似于定理2.13的证明,只需构造一个具体的模型(W,R1,…,Rm,V)使用反模型的方法,就可以证明它是CnEmT-模型,并且它是公理A5的反模型。
定理2.22 系统CnEm4(1≤n<ω)是CnEmT(1≤n<ω)的真扩张。
证明:由定理2.21和真扩张的定义可得。
(5)弗协调多主体认知逻辑CnEm4G(1≤n<ω)
CnEm4G(1≤n<ω)是在CnEm4(1≤n<ω)的基础上,通过增加多主体认知公理(A6)PiKiA→KiPiA(i=1,…,m且m∈N)而得到的。
CnEm4G(1≤n<ω)的公理(模式)如下:
①CnEm4(1≤n<ω)的全部公理(模式);
②A6 PiKiA→KiPiA(i=1,…,m且m∈N)。
CnE4(1≤n<ω)的推理规则如下:
R1(分离规则) 由A和A→B可推出├B;
R2(认知概括规则) 由A可推出KiA(i=1,…,m且m∈N)。
由以上CnEm4G(1≤n<ω)的公理(模式)模式和推理规则可知,系统CnEm4G(1≤n<ω)是系统CnEm4(1≤n<ω)的直接扩张。因而,CnEmK-定理、CnEmT-定理和CnEm4-定理也都是CnEm4G-定理。
定理2.23 CnEm4G(1≤n<ω)是可靠的,即:
①若Γ├CnEmGA,则Γ CnEmGA;②若├CnEmGA,则
CnEmGA;②若├CnEmGA,则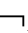 CnEmGA。
CnEmGA。
证明:类似于定理2.9的证明,略。
引理2.15 F*=(W*,R*1,…,R*m)是一个CnEm4G-框架。
证明:证F*是一个CnEm4G-框架,也即是要证F*是一个弱有向框架,只需证F*满足:A X1A X2A X3∈W*(X1R*iX2∧X1R*iX3)→E X′∈W*(X2R*iX′∧X′R*iX3)这等价于需证,对于A X1A X2A X3∈W*有:
X1R*iX2∧X1R*iX3→E X′∈W*(X2R*iX′∧X′R*iX3)
→({A:KiA∈X1}≤X2)∧({A:KiA∈X1}≤X3)→
E X′∈W*({A:KiA∈X2}≤X′)∧({A:KiA∈X′}≤X3)
→({PiA:A∈X2}≤X1)∧({A:KiA∈X1}≤X3)→
E X′∈W*({A:KiA∈X2}≤X′)∧({PiA:A∈X3}≤X′)
→({PiA:A∈X2}≤X1)∧({A:KiA∈X1}≤X3)→
E X′∈W*({A:KiA∈X2}∪{PiA:A∈X3}≤X′)
如果可以证明公式集{A:KiA∈X2}∪{PiA:A∈X3}是足道的,那么根据极大足道集扩张引理,就总是可以将公式集{A:KiA∈X2}∪{PiA:A∈X3}扩张成为一个极大足道集Γ,Γ属于极大足道集的集合max(即∈W*),且足道集{A:KiA∈X2}∪{PiA:A∈X3}又总是属于Γ的,所以就可以将Γ视为X′,也即这样的X′总是存在的。所以,为证F*是一个弱有向框架,只需证公式集{A:KiA∈X2}∪{PiA:A∈X3}是足道的。
假设X1R*iX2∧X1R*iX3,也即假设了({A:KiA∈X1}≤X2)∧({A:KiA∈X1}≤X3),也即假设了({PiA:A∈X2}≤X1)∧({A:KiA∈X1})≤X3。使用反证法,假设公式集{A:KiA∈X2}∪{PiA:A∈X3}是不足道的,也即假设了在公式集{A:KiA∈X2}中有B1,…,Bj且在公式集{PiA:A∈X3}中有C1,…,Ck使得├~(B1∧…∧Bj∧C1∧…∧Ck),这等价于├B1∧…∧Bj→~(C1∧…∧Ck)。
因此,根据定理2.4①,可得├KiB1∧…∧KiBj→Ki~(C1∧…∧Ck);由KiB1,…,KiBj∈X2,可得KiB1∧…∧KiBj∈X2;根据引理2.2⑥,就可得Ki~(C1∧…∧Ck)∈X2。
那么由假定{PiA:A∈X2}≤X1,可得PiKi~(C1∧…∧Ck)∈X1;由公理A6,根据引理2.2⑥,可得KiPi~(C1∧…∧Ck)∈X1;再由假定{PiA:A∈X3},可得Pi~(C1∧…∧Ck)∈X3,即,~Ki(C1∧…∧Ck)∈X3;但是,Ki(C1∧…∧Ck)∈X3。根据引理2.2②,这是不可能的。
所以,假设公式集{A:KiA∈X2}∪{PiA:A∈X3}不足道是不成立的。因此,F*是一个弱有向性框架。也即,F*是一个CnEm4G-框架。
引理2.16 M*=(W*,R*1,…,R*m,V*)是一个CnEm4G-模型。
证明:由引理2.15可知,F*=(W*,R*)是一个CnEm4G-框架;又由引理2.8可知V*满足赋值定义2.4的①—⑧。所以,M*是一个CnEm4G-模型。
定理2.24 CnEm4G(1≤n<ω)是完全的,即:
①如果Γ├CnEm4GA,那么Γ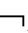 CnEm4GA;②如果├CnEm4GA,那么
CnEm4GA;②如果├CnEm4GA,那么 CnEm4GA。
CnEm4GA。
证明:设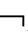 CnEm4GA,也即,A是CnEm4G有效的,则有
CnEm4GA,也即,A是CnEm4G有效的,则有
 在任意一个CnEm4G-框架上有效 (框架类有效定义)
在任意一个CnEm4G-框架上有效 (框架类有效定义)
 在任意一个CnEm4G-模型上有效 (模型类为真定义)
在任意一个CnEm4G-模型上有效 (模型类为真定义)
 在M*中为真 (M*是CnEm4G-模型)
在M*中为真 (M*是CnEm4G-模型)
 X∈max[V*(A,X)=1] (模型为真定义)
X∈max[V*(A,X)=1] (模型为真定义)
 X∈max(A∈X) (V*的定义)
X∈max(A∈X) (V*的定义)
→├CnEm4GA (引理2.5)
定理2.25 公理A6不是CnEm4G-定理。
证明:类似于定理2.13的证明,只需构造一个具体的模型(W,R1,…,Rm,V)使用反模型的方法,就可以证明它是CnEm4-模型,并且它是公理A6的反模型。
定理2.26 系统CnEm4G(1≤n<ω)是CnEm4(1≤n<ω)的真扩张。
证明:由定理2.25和真扩张的定义可得。
[1]冯棉:《可能世界与逻辑研究》,华东师范大学出版社1996年版。
[2]周北海:《模态逻辑导论》,北京大学出版社1997年版。
[3]张清宇:《弗协调逻辑》,中国社会出版社2003年版。
[4]弓肇祥:《认知逻辑新发展》,北京大学出版社2004年版。
[5]Li Na,Hao Xu-dong:A Paraconsistent Epistemic Logic System CnEK,《南京大学学报》(数学半年刊)2007年1月。
[6]郝旭东、李娜:《弗协调单主体认知逻辑系统CnEK及其扩张》,《重庆工业学院学报》(社会科学版)2009年第2期.
[7]Gabby,D.and Guenthner,F.:Handbookof Philosophical Logic,Second Edi-tion,Boston:Kluwer Academic Publishers,2002,Volume 6:287—394.
[8]Lou.Goble:The Blackwell Guide to Philosophical Logic,Blackwell Publishers Ltd,2002.
[9]N.C.A.da Cosda,O.Bueno,and A.G.Volkov:Outlines on a paraconsistent category theory,In P.Weingartner(ed.),Alternative Logics:do sciences need them?Springer,2004.pp.95—114.
(作者单位:华东师范大学哲学系)
【注释】
(1)本文由华东师范大学冯契基金和上海高校选拔培养优秀青年教师科研基金项目(79301601)资助完成。
(2)参见弓肇祥:《认知逻辑新发展》,北京大学出版社2004年版,第152—154页。
(3)郝旭东、李娜:《弗协调单主体认知逻辑系统CnEK及其扩张》,《重庆工业学院学报》(社会科学版)2009年第2期.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。














