对个人偏好的限制

第十五章　公共选择经济学中的循环问题

前文介绍直接民主制中的公共选择问题时曾经粗略地介绍过循环问题，在介绍代议民主制中的公共选择问题时也曾经强调，学者们的分析同样有陷入循环问题的可能性，可以说，循环问题一直困扰着那些研究后立宪阶段公共选择问题的经济学家。但是，无论如何，类似的困扰仅仅代表着学者们按照公共选择经济学的逻辑线索尝试对现实的政治生活进行理论分析时所面临的窘境。塔洛克曾经指出，现实的政治生活仿佛并没有像公共选择经济学预期的那样经常地陷入循环问题之中。

第一节　直接民主制中的循环问题

前文在介绍直接民主制中的公共选择问题，特别是对单峰偏好假设进行讨论的时候曾经指出，依照公共选择经济学固有的逻辑线索，学者们不得不经常地面对循环问题，出现循环问题时委员会将陷入无休止的讨论僵局之中。下面我们先来简单回顾一下，一些公共选择经济学家在直接民主制框架下讨论相关问题时所遇到的循环问题。

一、关于循环问题的简单回顾

邓肯·布莱克（1948a）提出了公共选择经济学的一个早期的重要定理，他指出，如果所有投票人的偏好在单一的议案维度上都是单峰的，采用简单多数规则将会产生一个均衡的投票结果。今天，布莱克的研究成果被归纳总结为一维议案的中位数投票人定理（定理7.1）。前文第七章曾经讨论了，如果单峰偏好假设不能够得到满足，那么，委员会的投票过程就很有可能会陷入一种无休止的循环之中，这时，对于任意一项备选议案x，都能够找到某一其他备选议案x′，使得委员会就x和x′两项议案进行投票时，有x′战胜x。当然，我们也曾经指出，单峰偏好假设并不是简单多数规则约束下均衡投票结果存在的必要条件。

回顾前文曾经列举过的一个简单例子。假设有a、b、c三位投票人就x、y、z三项备选议案进行投票，委员会希望借助简单多数规则帮助确定最终获胜议案。假设a关于三项备选议案的偏好序为xayaz；b关于三项备选议案的偏好序为ybzbx；c关于三项备选议案的偏好序为zcxcy。由上述三位投票人的偏好序可知，无论在一维的坐标轴上怎样排列x、y、z三项备选议案，总会存在一位投票人的偏好序违背单峰偏好假设。我们无法找到一个议案维度，使得在这个议案维度上描述x、y、z三项备选议案的时候，每一位投票人的偏好都能够满足单峰偏好假设的要求。当委员会就x和y两项备选议案进行讨论时，a和c两位投票人会投票赞成议案x；当委员会就x和z两项备选议案进行讨论时，b和c两位投票人会投票赞成议案z；当委员会就y和z两项备选议案进行讨论时，a和b两位投票人会投票赞成议案y。可见，在简单多数规则的约束下，当委员会就任意两项备选议案进行投票时，没有一项备选议案是不能被打败的，投票结果将会在x、y、z三项备选议案中间转来转去，从而导致循环问题^[1]的出现。

二、互投赞成票与循环问题

前文分析投票过程时总是假定，所有投票人都诚实地根据自己的偏好情况进行投票。但是，一些公共选择经济学家已经注意到，委员会存在着互投赞成票的可能性，那是一些违背自己真实的偏好情况，而选择“你投我偏爱的议案一票，我投你偏爱的议案一票”的非正规过程。

假设委员会由a、b、c三位投票人组成，他们根据简单多数规则组织投票过程，以便决定X和Y两项备选议案是否能够得以通过并颁布实施。当X或者Y不能得以通过时，我们就得到了另外两项备选议案－X或者－Y，其中－X否定了X，－Y否定了Y。如果X或者Y最终得以通过，则a、b、c三位投票人的利益变化情况如表15-1所示：

表15-1　议案的通过与投票人的利益变化情况

进一步考虑表15-1，如果所有投票人针对每一项备选议案都能够诚实地显示自己的偏好情况，那么，a关于X、Y、－X和－Y四项备选议案的偏好序可以表示为－XaX，－YaY；b关于X、Y、－X和－Y四项备选议案的偏好序可以表示为Xb－X，－YbY；c关于X、Y、－X和－Y四项备选议案的偏好序可以表示为－XcX，Yc－Y。此时，a会对X和Y两项备选议案都投反对票；b会对议案X投赞成票，而对议案Y投反对票；c会对议案X投反对票，而对议案Y投赞成票。因此，如果a、b、c三位投票人都能够诚实地显示自己关于X、Y、－X和－Y四项备选议案的偏好情况，那么，X和Y中的每一项备选议案都只能得到一张赞成票，在简单多数规则的约束下，X和Y两项备选议案都不能够在委员会的讨论中获得通过。此时，我们用（－X，－Y）来代表委员会的投票结果。假设经济的初始状态是（－X，－Y）。如果X和Y两项备选议案在委员会的讨论过程中都没能获得通过，此时，经济将保持原来的状态不变，a、b、c三位投票人的利益变化幅度都会是0。

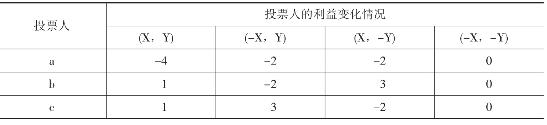
除了（-X，-Y）以外，委员会关于X、Y、－X和－Y四项备选议案的投票结果还可能会是：X和Y两项备选议案全部通过委员会的讨论，我们用（X，Y）予以表示；X和Y两项备选议案中只有一项通过了委员会的讨论，我们用（－X，Y）表示只有议案Y获得通过的情况，用（X，－Y）表示只有议案X获得通过的情况。对应上述四种投票结果，求解a、b、c三位投票人的利益变化情况，如表15-2所示。

根据表15-2，委员会在考量（－X，－Y）和（X，Y）两种投票结果的时候，与（－X，－Y）相比，b和c两位投票人更希望委员会的投票结果是（X，Y）。在简单多数规则的约束下，为了使投票结果（X，Y）得以实现，

表15-2　投票结果与投票人的利益变化情况

b必须隐瞒自己真实的偏好序－YbY，他会为议案Y投赞成票以换取投票人c为议案X投赞成票；c也必须隐瞒自己真实的偏好序－XcX，他会为议案X投赞成票以换取投票人b为议案Y投赞成票。此时，就出现了令经济学家感兴趣的互投赞成票现象。重新考虑表15-1，当委员会就X和－X两项备选议案进行讨论的时候，有a和c两位投票人会投票支持议案－X，根据简单多数规则，－X将战胜X而获得通过，委员会的排序满足－XX。当委员会就Y和－Y两项备选议案进行讨论的时候，有a和b两位投票人会投票支持议案－Y，根据简单多数规则，－Y将战胜Y而获得通过，委员会的排序满足－YY。但是，当所有投票人进一步就（－X，－Y）和（X，Y）两种投票结果进行选择的时候，就会有b和c两位投票人通过互投赞成票力图促使投票结果（X，Y）得以实现，根据简单多数规则，（X，Y）将战胜（－X，－Y），委员会的排序满足（X，Y）（－X，－Y）。更为一般地，公共选择经济学认为，当委员会关于任意四项备选议案X、Y、－X和－Y的排序满足－XX，－YY且（X，Y）（－X，－Y）时，我们就说，委员会组织的投票过程中存在着互投赞成票现象。与前文讨论的X、Y、－X和－Y四项备选议案相类似，其中－X否定了X，而－Y否定了Y。

在简单多数规则的约束下，进一步分析表15-2所描述的情况，我们可以发现，（X，Y）也不能够成为委员会的最终投票结果，因为与（X，Y）相比，a和c两位投票人更希望投票结果（－X，Y）能够实现，此时委员会的排序满足（－X，Y）（X，Y）；而a和b两位投票人更希望投票结果（X，－Y）能够实现，此时委员会的排序满足（X，－Y）（X，Y）。当然，（－X，Y）和（X，－Y）中的任意一项也都不能够成为委员会的最终投票结果，因为与（－X，Y）相比，a和b两位投票人更希望投票结果（－X，－Y）得以实现，此时委员会的排序满足（－X，－Y）（－X，Y）；而与（X，－Y）相比，a和c两位投票人更希望投票结果（－X，-Y）得以实现，此时委员会的排序满足（－X，－Y）（X，－Y）。（－X，－Y）也不能够成为委员会的最终投票结果，因 为按照前文的分析，b和c两位投票人会选择互投赞成票并促使投票结果（X，Y）得以实现，此时委员会的排序满足（X，Y）（－X，－Y）。通过以上分析，我们可以发现，在（X，Y），（－X，Y）或者（X，－Y），与（－X，－Y）之间存在着一个完整的投票循环，委员会将陷入无休止的讨论之中，从而无法得出确定的投票结果。

伯恩霍尔兹（1973）曾经论证，除非采用一致性规则，否则，互投赞成票现象的出现就意味着委员会的讨论将会陷入循环问题之中。在展开论述之前，伯恩霍尔兹希望约束每一位投票人的偏好序，使之满足独立性假设。独立性假设要求，对于任意一位投票人i，i关于任意一对备选议案X和－X的偏好序与任何其他备选议案Y无关，如果i的偏好序能够满足Xi－X，也一定能够满足（X，Y）i（－X，Y），其中－X否定了X。在此基础上，伯恩霍尔兹尝试证明下述定理：

定理15.1：如果某一投票过程出现互投赞成票现象，就意味着委员会的排序一定不满足传递性假设；如果委员会的排序能够满足传递性假设，就意味着该投票过程一定不会出现互投赞成票现象。

下面依照伯恩霍尔兹的逻辑，简单介绍上述定理的证明过程。

首先，我们来尝试证明第一个命题：互投赞成票现象的存在意味着委员会的排序一定不满足传递性假设。

假设某一投票过程中出现互投赞成票现象，使得委员会的排序满足：

－XX

－YY

（X，Y）（－X，－Y） 　　　　　　（15.1）

因为在委员会的讨论过程中出现了互投赞成票现象，所以，一定可以找到某一取胜联盟h，^[2]使得该取胜联盟对于判定委员会的排序情况具有决定性作用，并且对于h中的所有投票人都有如下形式的偏好序：

－XhX

－YhY

（X，Y）h（－X，－Y） 　　　　　　（15.2）

根据独立性假设，取胜联盟h中所有投票人的偏好序一定还能够满足下式：

（－X，－Y）h（X，－Y）

（X，－Y）h（X，Y） 　　　　　　（15.3）

又因为取胜联盟h对于判定委员会的排序情况具有决定性作用，只要h中所有投票人的偏好序都采取如（15.3）式的形式，就能够迫使委员会的排序满足：

（－X，－Y）（X，－Y）

（X，－Y）（X，Y） 　　　　　　（15.4）

由（15.1）式和（15.4）式可知，出现互投赞成票现象的时候，委员会的排序不满足传递性假设的要求。

其次，我们来尝试证明定理的第二个命题：如果委员会的排序能够满足传递性假设，就意味着该投票过程一定不会出现互投赞成票现象。

假设对于备选议案X和－X，Y和-Y，其中－X否定了X，-Y否定了Y，委员会的排序能够满足：

－XX

－YY 　　　　　　（15.5）

令h是一个取胜联盟，使得该取胜联盟对于判定委员会的排序情况具有决定性作用，并且，h中所有投票人的偏好序都可以表示成如下的形式：

－XhX

－YhY 　　　　　　（15.6）

根据独立性假设，h中所有投票人的偏好序还能够满足：

（－X，Y）h（X，Y）

（－X，－Y）h（－X，Y） 　　　　　　（15.7）

又因为取胜联盟h对于判定委员会的排序情况具有决定性作用，只要h中所有投票人的偏好序都采取如（15.7）式的形式，就能够迫使委员会的排序满足下式：

（－X，Y）（X，Y）

（－X，－Y）（－X，Y） 　　　　　　（15.8）

如果委员会的排序能够满足传递性假设的要求，则根据（15.8）式，这一排序可以被表示为：

（－X，－Y）（－X，Y）（X，Y） 　　　　　　（15.9）

根据（15.5）式和（15.9）式，当委员会的排序能够满足传递性假设时，一定不会出现互投赞成票现象。

第二节　代议民主制中的循环问题

前文采用宿命论的投票行为假设构造两党竞争模型时曾经提到，该模型的结论能否成立还要依赖于一些基本的假设条件，比如所有选民的政治主张以及候选人的竞选纲领都可以在一维的意识形态光谱上予以表示，比如所有选民的偏好都能够满足单峰偏好假设。如果放松这些假设条件，在两党竞争的框架下讨论公共选择问题时，学者们仍然不得不面对循环问题，只不过与直接民主制条件下讨论的循环问题相比较，人们在代议民主制条件下所讨论的循环问题其表现形式会有所不同。

假设有a和b两位候选人代表两个政党参与竞选，他们提出自己的竞选纲领以求争得更多选民的支持，并进一步达到当选的目的。假设经济中只存在x、y和z三位选民，他们通过参与某一投票过程来决定a和b两位候选人的当选情况，且该投票过程采用简单多数规则。假设选民们只对X、Y、Z三项备选议案感兴趣，且三项议案的颁布实施将会给三位选民带来不同幅度的利益变化，如表15-3所示：

表15-3　备选议案的实施与选民利益的变化情况

因此，a和b两位候选人的竞选纲领可以被简单地描述成，关于自己当选之后将会颁布和实施哪些议案的承诺。进一步考察表15-3，当X、Y、Z三项议案全部得以颁布实施时，x、y和z三位选民的利益总和将会达到最大值。但是，a和b两位候选人为了赢得选举的胜利是不会选择把支持所有备选议案当作自己的竞选纲领的。如果其中的某一位候选人承诺自己当选之后，X、Y、Z三项议案都会得以颁布和实施，在简单多数规则的约束下，另一位候选人只要选择支持其中的任意两项议案就能够得到两位选民的选票而顺利当选。如果候选人a决定支持X和Y两项议案，在简单多数规则的约束下，b只要选择支持Y和Z两项议案，就能够得到y和z两位选民的选票，从而击败a并获得竞选的胜利；如果候选人b决定支持Y和Z两项议案，在简单多数规则的约束下，a只要选择支持X和Z两项议案，就能够得到x和z两位选民的选票，从而击败b并获得竞选的胜利；如果候选人a决定支持X和Z两项议案，在简单多数规则的约束下，b只要选择支持X和Y两项议案，就能够得到x和y两位选民的选票，从而击败a并获得竞选的胜利。当然，某一位候选人选择支持X、Y、Z中任意一项备选议案的竞选纲领也是不可行的，这将会使得他的竞选对手有机会支持另外两项议案，进而得到两位选民的选票并获得竞选胜利。由此可见，候选人提出的每一个竞选纲领都有可能被另一位候选人提出的其他竞选纲领所击败，上述集体选择过程将会陷入循环问题之中。

通常情况下，公共选择经济学家会预期，直接民主制条件下集体选择过程中出现的循环问题可能会导致委员会在不同的备选议案之间转来转去，代议民主制条件下两党竞争中出现的循环问题则呈现出略为不同的表现形式，在这里，循环表现为当选后的候选人——在本书中也把他们称为政治家，通常是执政者——在多期选举中的不断落选。

第三节　为什么如此稳定

无论公共选择经济学家在他们所构建的理想世界里是如何描述循环问题的，在现实的政治生活中，委员会的投票过程并没有频繁地陷入无休止的讨论僵局之中，也没有出现当选后的政治家在多期选举中的不断落选现象。我们身处其中的政治过程通常是稳定的，并没有像公共选择经济学家所预期的那样，经常性地陷入循环问题之中。这种情况受到戈登·塔洛克（1981）的关注，他提出的疑问是——为什么如此稳定？

学者们还试图进一步探讨，怎样才能帮助公共选择经济学摆脱循环问题的困扰，使它能够更好地解释现实的政治过程。我们在前文曾经介绍过的中位数投票人定理和简单多数规则定理在某种程度上反映了学者们为解决上述问题所做的努力，他们尝试限制所有投票人或者选民的偏好类型，希望能够借此避免循环问题的出现。除此以外，一些公共选择经济学家还试图通过对投票过程中可能会出现的若干因素做进一步的研究，希望能够帮助公共选择经济学绕开循环问题。当然，其中有些学者关注的焦点在于揭示投票程序中存在的诸多不合理因素，虽然人们常常把他们的研究成果看做是为绕开循环问题所做的努力。

一、对个人偏好的限制

无论我们是否注意到，依照公共选择经济学的逻辑线索所推得的循环问题与政治现实之间存在着巨大的差距，出现循环问题都不是令人愉快的。前文第七章曾经讨论过的中位数投票人定理和简单多数规则定理希望通过限制某些类型的偏好序同时出现在委员会中，以便绕开循环问题并帮助委员会挑选出最终获胜的议案。另外，第十四章在介绍阿罗不可能定理的时候也曾经提到，在阿罗看来，现实生活中可能会存在这样一些个人，他们意识到自己的偏好类型不能被社会所容许，因此，很有可能选择在一开始就隐瞒自己真实的偏好情况。这样看来，一些公共选择经济学家所采取的对个人偏好施加适当限制的做法也许并不是完全没有现实意义的。

二、议程控制

理查德·麦凯尔维（1976）分析了在现实的投票过程中经常会出现的议程控制问题，他的论述旨在说明，如果委员会按照简单多数规则组织的投票过程中出现循环问题，能够控制投票议程的个人就有能力让他所选定的任何一项备选议案成为委员会最终获胜的议案。但是，对于那些急于绕开循环问题的经济学家，麦凯尔维的论述也许还意味着，赋予某个人控制议程的权力，可以帮助委员会避免循环问题的出现，并且挑选出某项议案使之成为最终获胜的议案。

假设存在一个由a、b、c三位投票人组成的委员会，三位投票人的理想议案分别是Xa、Xb和Xc。令议案X代表经济的初始状态，X通常也被看做是委员会讨论的起点。假设存在X1和X2两个议案维度，并且在X1－X2议案空间中，所有投票人的无差异曲线都是圆的，每一位投票人都更偏爱与自己的理想议案位置更加接近的备选议案。如图15-1所示。

图15-1　关于议程控制的分析

在X1－X2议案空间中寻找a、b、c三位投票人理想议案Xa、Xb和Xc的位置，连接其中的任意两点可以发现，Xa、Xb和Xc恰好构成某个三角形的顶点。前文曾经提到，公共选择经济学认为，在简单多数规则的约束下，当三位投票人的理想议案在x1－x2议案空间中的位置构成某个三角形的顶点时，委员会的讨论就会陷入循环问题之中。假设a提交委员会讨论的议案是Xa，那么，b和c两位投票人就会有动力在图15-1中的XbXc线段上寻找到某一备选议案Xbc，因为与Xa相比较，Xbc与b和c两位投票人理想议案Xb和Xc的位置更加接近，所以，Xbc能够获得b和c的支持进而战胜Xa。但是，Xbc也不能成为最终获胜的议案，因为a会选择拉拢b和c中的某一位投票人，比如b，此时a和b会在线段XaXb上寻找到某一备选议案Xab，使得与Xbc相比较，Xab与a和b两位投票人理想议案Xa和Xb的位置更加接近，所以，Xab能够获得a和b的支持进而战胜Xbc。同理，Xab也不能成为最终获胜的议案，因为c会选择拉拢a和b中的任意一位投票人，比如a，此时a和c会在线段XaXc上寻找到某一备选议案Xac，使得与Xab相比较，Xac与a和c两位投票人理想议案Xa和Xc的位置更加接近，所以，Xac能够获得a和c的支持进而战胜Xab。由此可见，在x1－x2议案空间中的任意一项备选议案都能够被其他备选议案打败，委员会的投票过程将会陷入循环问题之中。

当存在循环问题的时候，假设有某位个人i，i拥有控制议程的权力，他可以决定哪些议案能够提交委员会讨论，并且为每一项备选议案安排投票日程。假设i的理想议案为Xi，Xi的位置如图15-1所示。当经济处于起点X时，根据个人i的安排，委员会就X和X1两项备选议案组织第一轮投票，因为与X相比较，X1与b和c两位投票人理想议案Xb和Xc的位置更加接近，所以，X1能够在委员会的讨论中获胜。以X1为起点，根据个人i的安排，委员会就X1 和X2两项备选议案组织第二轮投票，因为与X1相比较，X2与a和c两位投票人理想议案Xa和Xc的位置更加接近，所以，X2能够在委员会的讨论中获胜。上述过程不断持续下去，i能够凭借控制议程的权力使得自己的理想议案Xi成为最终获胜的议案，无论Xi在X1－X2议案空间中的位置如何。

无论如何，通过议程控制的办法绕开循环问题，是不能令人感到愉快的。当然，如何帮助公共选择经济学摆脱循环问题的困扰，这也许并不是麦凯尔维关注的焦点，他分析的是投票过程中出现议程控制所导致的不良后果，并且建议对那些有权安排投票议程的人有所监督。

三、一次只对一个维度投票

为了摆脱循环问题的困扰，有些公共选择经济学家建议约束委员会，使之每次只能针对一个议案维度组织投票。当然，这里仍然假设，在每一个议案维度上，所有投票人的偏好都能够满足单峰偏好假设。利用图15-1描述的例子，在这个例子中存在X1和X2两个议案维度，如果不采取任何形式的限制，委员会的讨论过程将难以避免陷入循环问题之中。如果接受一些学者的建议，每次只针对一个议案维度组织投票，则有图15-2：

图15-2　一次只对一个维度投票

如图15-2所示，当人们针对X1这一单一维度进行投票的时候，a在这一议案维度上就成为中位数选民，他的选择X1a将战胜所有其他的备选议案，并且在委员会的讨论中获得通过。当人们针对X2这一单一维度进行投票的时候，b在这一议案维度上就成为中位数选民，他的选择X2b将战胜所有其他的备选议案，并且在委员会的讨论中获得通过。因此，有些经济学家指出，在多维议案空间中，采用“一次只对一个维度投票”的办法，能够帮助我们绕开循环问题。在图15-2所描述的例子中，经济最终会离开初始位置X，向Xe移动。

当然，人们对于“一次只对一个维度投票”这一建议也提出了一些质疑。在图15-2中，如果能够把X1和X2两个议案维度理解为两种不同的公共物品的供给数量，这正是一些公共选择经济学家进行类似的分析时所做的假设，那么，我们可以要求委员会按照上述建议——“一次只对一个维度投票”——组织投票过程。但是在很多时候，“一次只对一个维度投票”的建议看起来是缺乏现实性的。委员会所讨论的问题常常不能够在不同的议案维度上进行分解，因此也就无法做到“一次只对一个维度投票”。当然，类似的分析还依赖于关于投票人的行为假设，即投票人在针对一个议案维度进行投票的时候，完全不会考虑到自己以及其他投票人在另一个议案维度上的偏好情况。

四、互投赞成均衡

除此以外，一些经济学家还对互投赞成票现象做了进一步分析，希望能够借此摆脱循环问题的困扰。

回顾前文分析互投赞成票现象时所列举的简单例子。假设委员会采用简单多数规则，由a、b、c三位投票人通过投票决定，X、Y、－X、－Y四项备选议案中的哪些议案能够得以通过并颁布实施，其中－X否定了X，－Y否定了Y。前文用表15-1和表15-2概括了每一位投票人的利益变化情况和委员会可能颁布实施的各种投票结果，并且通过分析指出，委员会关于X、Y、－X、－Y四项备选议案的讨论过程中有出现互投赞成票现象的可能性，在投票结果（X，Y）、（－X，Y）或者（X，－Y）与（－X，－Y）之间存在一个完整的投票循环。

有些经济学家指出，上述分析依赖关于投票人行为的一个假设条件，即所有投票人都是“近视”的，他们过于重视眼前发生的事情，往往“看不清”由自己的行为所引致的长期后果。在这些学者看来，伯恩霍尔兹得出的结论似乎略显武断。

以投票结果（－X，Y）为例，（－X，Y）是由a和c两位投票人结成联盟迫使b同意的结果。但是，a和c之间的联盟是不稳定的，根据表15-2，处于ac联盟中的投票人c已经得到了他可能得到的最大利益，一旦c选择离开ac联盟，无论是与b结成联盟，还是不与任何投票人结成联盟，都只能使他的利益水平有所下降。而处于ac联盟中的投票人a，如果选择离开ac联盟，无论是与b结成联盟，还是不与任何投票人结成联盟，都不能降低a的利益水平。因此，c必须随时面对a拆散ac联盟的威胁，ac联盟进而投票结果（－X，Y）不是一个稳定的均衡。考虑另一个投票结果（X，－Y），（X，－Y）是由a和b两位投票人结成联盟迫使c同意的结果。处于ab联盟中的投票人a将会与ac联盟中的投票人a面临完全相同的情况，而投票人b将会与ac联盟中的投票人c面临完全相同的情况，可见，b也必须随时面对a拆散ab联盟的威胁，ab联盟进而投票结果（X，－Y）也不是一个稳定的均衡。但是学者们认为，投票结果（X，Y）会是一个稳定均衡，（X，Y）是由b和c两位投票人结成联盟迫使a同意的结果。对于b和c中的任意一位投票人，只要他能与a结成联盟，就能使自己的处境变得更好，可见，b和c两位投票人都面临着对方拆散bc联盟的威胁，一旦有人试图拆散bc联盟，他在联盟中的伙伴也会做出完全相同的选择并与a结成联盟。因为b和c都认识到这一点，所以每一个人都会选择继续维持bc联盟，从而使得b和c通过互投赞成票得出的投票结果（X，Y）在委员会的讨论中获得通过。

当然，学者们也认识到，即便承认bc联盟在一定程度上是稳定的，也不能否认与a结成联盟进而争取更高水平的利益对于b和c两位投票人的诱惑，或许应该把投票结果（X，Y）看做是a、b、c三位投票人之间无限次重复博弈的均衡解。

第四节　简单评价

詹姆斯·布坎南曾经批评阿罗的一般可能性定理，认为阿罗的全部努力都在于寻找某种形式的社会福利函数。但是，通过前文的介绍我们可以发现，公共选择经济学中的循环问题与阿罗的一般可能性定理针对的是一些相同的问题。其中，循环问题可以被表述为，按照某一投票规则，通常是简单多数规则，从参与集体选择的个人出发可能无法得出某一确定的政治结果，当人们尝试在社会整体上为各种可能的政治结果排序时，往往不满足传递性假设的要求。而阿罗的视角则更加宽泛，他按照福利经济学的语言把这一问题表述为无法找到任何机制，包括各种形式的投票规则，使得我们可以依靠这种机制从所有个人的偏好序入手得出令人满意的“社会序关系”，即社会福利函数。由于公共选择经济学与阿罗代表的新福利经济学有着共同的“经济人”假设和方法论个人主义原则，采用的也都是西方主流经济学的研究方法，当二者关注相同的问题时，从他们的逻辑起点、分析过程和得出的结论来看，都不难找到共同点。在这里，公共选择经济学与新福利经济学就遇到了相似的困境。虽然阿罗把自己的努力局限于福利经济学的研究框架，他更加关注寻找某种形式的社会福利函数问题，公共选择经济学家的努力其目的在于解释个人对于集体选择过程的参与及其导致的政治结果。

无论如何，正像戈登·塔洛克指出的，现实的政治过程得出的结果往往是稳定的，并没有像一些公共选择经济学家所预期的那样经常地陷入循环问题之中。当然，也有一些学者，包括塔洛克在内，他们遵循公共选择经济学的逻辑框架试图摆脱循环问题所造成的困扰，进而弥补理论与现实之间的巨大鸿沟。通过前文对这些学者研究成果的简单介绍可以发现，他们的努力并没能做到完全消除人们心中的疑惑。

为什么会出现循环问题呢？公共选择经济学家的理论分析与政治领域中的现实状况之间的巨大差异又说明了什么呢？是哪一个环节出现了失误，还是在一开始就误入歧途了呢？所有这些疑问困扰着公共选择经济学家，也许在某种程度上还影响着公共选择经济学本身的发展。

基本概念和术语

循环问题　互投赞成票　独立性假设　议程控制

思考题

1．请简单介绍公共选择经济学中的循环问题，并进一步分析，循环问题对于公共选择经济学意味着什么。

2．请简单介绍不同的学者在公共选择经济学的研究框架下为避免相关的讨论陷入循环问题所做的努力。

【注释】

[1]前文也曾经提到，如果按照肯尼思·约瑟夫·阿罗的表述，这里所说的循环问题应该被称为投票悖论。本书用投票悖论来特指一种关于选民投票行为的质疑——为什么总是有成千上万的选民选择参与投票过程，虽然选民为此付出的成本往往要大于参与投票所带来的收益。

[2]在多数通过规则的约束下，h总是表现为某一多数联盟。