利息等值计算的基本类型,资金时间价值的计算

前面讲过，资金存在时间价值。实际上，资金的时间价值在银行就体现为存款或贷款利息（interest）。比如，将100元存入银行，存一年，若存款年利率为2.2%，那么一年后可以从银行取出102.2元，这2.2元的差额就是利息。

什么是利息呢？利息是指放弃资金的使用权应该得到的回报（如存款利息）或者指占有资金的使用权应该付出的代价（如贷款利息）。利息可以按年、季度、月、日等周期计算，这种计算利息的时间单位称为计息周期。为便于计算和学习，以下暂时假定利息的计息周期为年。

利息是根据利率来计算的。利率（interest rate）是一个计息周期内所得到的利息额与借贷资金额（即本金）之比，一般用百分比来表示。利率的表达式为

利息分单利和复利两种。

所谓单利（simple interest）就是指每期均按原始本金计算利息，利息不再计算利息。设P（present的第一个字母）代表原始本金，F（future的第一个字母）代表未来值，n代表计息期数（如年数、月数），i代表计息周期内的利率，I代表总的利息。则按照单利计算，n期内的总利息为

I=P×n×i

n期后的本利和应为

F=P+Pni=P（1+n×i）　　（2-1）

根据以上公式，可以绘制利息I和计息周期n的关系图，以及未来值F和计息周期n的关系图，分别如图2-5和图2-6所示。

图2-5　单利I和n的关系图

图2-6　单利F和n的关系图

从图2-5和图2-6可见，利息与计算利息的时间呈线性关系，未来值也与计算利息的时间呈线性关系。即不论计息周期n为多大，只有本金计算利息，而利息不再计算利息。

【例2-3】　某人存入银行2000元，年存款利率为2.8%，存3年，试按单利计算3年后此人能从银行取出多少钱（不考虑利息税）？

【解】　3年后的本利和为

F=P（1+n×i）=2 000×（1+3×2.8%）元=2 168元

即3年后此人能从银行取出2 168元钱。

所谓复利（compound interest）就是每期均按原始本金和上期的利息和来计算利息。也就是说，每期不仅要对本金计算利息，还要对利息计算利息，即所谓的“利滚利”。

仍采用单利的符号及含义，按照复利计算n期内每期的利息及本利和，见表2-2。

表2-2　复利的本利和计算表

因此，复利的计算公式为

F=P（1+i）n　　（2-2）

按照复利计算，n期末的利息为

I=F-P=P（1+i）n-P=P[（1+i）n-1]

根据以上两个公式，可以绘制利息I和计息周期n的关系图，以及未来值F和计息周期n的关系图，如图2-7和图2-8所示。

图2-7　复利I和n的关系图

图2-8　复利F和n的关系图

【例2-4】　本金为2 000元，年存款利率为2.8%，存3年，按复利计算3年后能从银行取出多少钱？

【解】　3年后复利的本利和为

F=P（1+i）n=2 000（1+2.8%）3元=2 172.75元

由以上的计算可知，在所有条件相同的情况下，一般按复利计算的利息大于按单利计算的利息。而且，时间越长，复利利息与单利利息的差别越大。这就是银行经营与生存的目的之一。个人在银行的存款利息是按单利计算，而银行借放贷的利息是按复利计算。

复利法能够较充分地反映资金的时间价值，也更符合客观实际。这是国内外普遍采用的计息方法，也是我国现行信贷制度正在推行的方法。工程经济分析中普遍采用复利计息。复利计息的计算按支付方式不同，归纳起来有如图2-9所示的几种类型的计算方式。

图2-9　复利等值计算的基本类型

1. 一次支付型

一次支付型（single-payment type）又称整付，是指项目在整个寿命期内，其现金流量无论是流入还是流出都只发生一次的情况。一般有两种情况：一种是发生在期初，一种是发生在期末，如图2-10所示。

图2-10　一次支付现金流量图

如果考虑资金的时间价值，若图2-10中的初始流出现金P刚好能被最终的收入补偿，那么就说P与F等值。一次支付型的计算公式有以下两个。

1）一次支付终值公式

一次支付终值公式（single-payment compound-amount formula）就是求终值。也就是说，在项目的初期投入资金P，n个计息周期后，在计息周期利率为i的情况下，需要多少资金来弥补初期投入的资金P呢？这个问题与复利本利和计算相同。因此，一次支付终值公式为

F=P（1+i）n　　（2-3）

由于式（2-3）中有高次方，因此，为计算方便，工程经济中常用系数来表示，使用时直接查附录中的复利终值系数表即可。把系数（1+i）n称为一次支付终值系数，使用符号（F/P，i，n）表示。即

F=P（1+i）n=P（F/P，i，n）

查阅时，先找（F/P，i，n）系数表，然后根据已知值P、i、n查找（F/P，i，n）的值。

【例2-5】　某企业向银行借款50 000元，借款时间为10年，借款年利率为10%，问10年后该企业应还银行多少钱？

【解】　此题属于一次支付型，求一次支付的终值。

F=P（1+i）n=50 000（1+10%）10元=129 687.12元

也可以查（F/P，i，n）系数表，得（F/P，i，n）=2.593 7，则

F=P（F/P，i，n）=50 000×2.593 7元=129 685元

两种计算方法所得结果的小差别是由于小数点的保留位数不同引起，不影响大局。

2）一次支付现值公式

一次支付现值公式（single-payment present-value formula）就是求现值。也就是说，项目在计息周期内利率为i的情况下，一次支付现值是一次支付n期末终值公式的逆运算。由式（2-3）可以直接导出

其中，系数1/（1+i）n称为一次支付现值系数，用符号（P/F，i，n）表示。为计算方便，可以查一次支付现值系数（P/F，i，n）表。查阅时，先找（P/F，i，n）系数表，然后根据已知值F、i、n查（P/F，i，n）的值。即

【例2-6】　小张希望3年后获得20 000元的资金，现在3年期年贷款利率为5%，那么小张现在贷款多少出去才能实现目标？

【解】　这是一次支付求现值型。

也可以查表（P/F，i，n）。

P=20 000×0.863 8元=17 276元

2. 多次支付型

多次支付的现金流量发生在多个时刻点上，而不是像前面两种支付那样只集中发生在期初或期末。多次支付型分多次等额支付型和多次不等额支付型两种。多次等额支付是指现金流量在各个时刻点等额、连续发生。多次等额支付型有以下4个计算公式。

1）等额支付终值公式

等额支付终值公式（uniform-payments compound-amount formula）是计算现金流量等额、连续发生在各个时刻点上，在考虑资金的时间价值情况下，各个时刻点的等额资金全部折算到期末，需要多少资金来与之等值，也就是说求等额支付的终值。等额支付的现金流量图如图2-11所示。

图2-11　等额支付的现金流量图

图2-11中，若已知等额支付值A，求终值F，可以利用一次支付终值的计算公式来求F值。图2-11中的每个A都相当于一次支付终值中的一个P，这样就把每个A折算成第n年末的终值，然后再把所有的终值相加，即可得等额支付的终值。即有

F=A+A（1+i）+A（1+i）2+…+A（1+i）n-2+A（1+i）n-1

可以利用等比数列求和的方法对上式求和，也可以利用代数方法求和。现在利用代数方法求和，用（1+i）去同时乘以上式的两端，上式变成如下形式。

F（1+i）=A（1+i）+A（1+i）2+A（1+i）3+…+A（1+i）n-1+A（1+i）n

然后将两示相减，得

F（1+i）-F=A（1+i）n-A

上式变形得

注意：该公式是对应A在第1个计息期末开始发生而推导出来的。

式（2-5）中的系数[（1+i）n-1]/i称为等额支付终值系数，用符号（F/A，i，n）表示。可以通过查书后附录中给出的等额支付终值系数（F/A，i，n）表来计算，方法是根据已知值A、i、n，查系数（F/A，i，n）的值。

【例2-7】　某人每年存入银行30 000元，存5年准备买房用，存款年利率为3%。问：5年后此人能从银行取出多少钱？

【解】　此题属于等额支付型，求终值。

也可以查表（F/A，i，n）求解，则有

F=A（F/A，i，n）=30 000×5.3091元=159 273元

2）等额支付偿债基金公式

等额支付偿债基金公式（uniform-payments repayment-fund formula）是指期末一次性支付一笔终值，用每个时刻点上等额、连续发生的现金流量来偿还，计算需要多少资金才能偿还F。或者说已知终值F，求与之等值的年值A，这是等额支付终值公式的逆运算。由式（2-5）可以直接导出：

式（2-6）中的系数i/[（1+i）n-1]称为等额支付偿债基金系数，可用符号（A/F，i，n）表示。可以通过查书后附录中给出的等额支付偿债基金系数（A/F，i，n）表来计算，方法是根据已知值F、i、n，查系数（A/F，i，n）的值。

【例2-8】　某人想在5年后从银行提出20万元用于购买住房。若银行年存款利率为5%，那么此人现在应每年存入银行多少钱？

【解】　此题属于求等额支付偿债基金的类型。

也可以查表计算：

A=F（A/F，i，n）=200 000×0.1810元=36 200元

3）等额支付现值公式

等额支付现值公式（uniform-payments present-value formula）是计算现金流量等额、连续发生在每个时刻点上，相当于期初一次性发生的多少现金流量。等额支付现值的现金流量图如图2-12所示。

图2-12　等额支付现值的现金流量图

图2-12中，若已知等额年值A，求现值P。图2-12中的每个A相对于P来说都是一个未来值。计算时可以每个A先折算到期初的现值，然后再求和。但这样算较麻烦，可以利用前面已经推导出的两个公式来直接计算。

前面已经推导出公式F=P（1+i）n和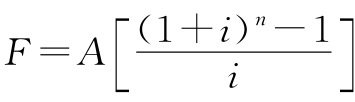，令两个公式相等，即可得出：

式（2-7）中的系数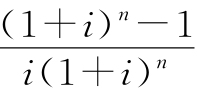称为等额支付现值系数，可用符号（P/A，i，n）表示。计算时也可以查书后给出的等额支付现值系数（P/A，i，n）表计算，方法是根据已知条件A，i，n查系数（P/A，i，n）的值。

【例2-9】　某人为其孩子上大学准备了一笔资金，打算让孩子在今后的4年中，每月从银行取出500元作为生活费。现在银行存款月利率为0.3%，那么此人现在应存入银行多少钱？

【解】　此题属于等额支付求现值型。

计息期n=4×12月=48月

也可以查表计算，但因利率太小，没有编制小利率系数表，故无法查阅。

4）等额支付资本回收公式

等额支付资本回收公式（uniform-payments capital recovery formula）是计算期初一次性发生一笔资金，用每个计息期等额、连续发生的年值来回收，所需要的等额年值是多少。这就相当于等额支付现值公式中，已知现值P求等额年值A。即

其中，式（2-8）中的系数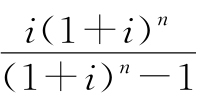称为等额支付资本回收系数，用符号（A/P，i，n）表示。计算时可以利用书后给出的系数表查表计算。

【例2-10】　某施工企业现在购买1台推土机，价值15万元。希望在今后8年内等额回收全部投资。若资金的折现率为3%，试求该企业每年回收的投资额。

【解】　这是一个用等额支付资本回收公式求每年的等额年值的问题。

也可以查系数表（A/P，i，n）计算，可得

A=150 000×0.142 5元=21 375元

3. 多次不等额支付型

多次不等额支付型（many unequal payments type）是指现金流量连续发生在多个时刻点上，但各个时刻点发生的现金流量不完全相等，如图2-13所示。为了推导通用的公式，下面仅讨论每个计息期发生的现金流量成等差和等比序列的情况。

图2-13　多次不等额支付型现金流量图

1）等差序列的等值计算

等差序列是指各期发生的现金流量成等差序列。假定第1个计息期末的现金流量为A1，以后每期递增G。即第2个计息期末的现金流量为A1+G，第3个计息期末的现金流量为A1+2G，依此类推，第n个计息期末的现金流量为A1+（n-1）G。现金流量图如图2-14所示，图中的现金流量A1、A1+（n-1）G、时间轴和连接各现金流量的箭头的虚线正好组成一个梯形。因此，等差序列的等值计算（calculation of equal difference-series equivalent）在一些书上称为均匀梯度系列公式。

图2-14　等差序列的现金流量图

如果能把图2-14中的现金流量转换成等额支付系列形式，那么根据等额支付终值公式和等额支付现值公式，很容易求得第n年末的将来值F和第0年的现值P。下面对图2-14进行分解，从现金流量A1箭头处画一条平行于时间轴的直线，这样图2-14就由两部分现金流序列组成：等额支付和等差支付。等差支付现金流量图变成图2-15的形式。计算时分别对等额支付和等差支付单独进行计算，然后求二者之和。

图2-15　不含等额支付的等差序列现金流量图

对于等额支付部分直接用前面的等额分付的终值公式计算将来值即可，其中的等额支付是A1。下面推导等差支付终值的公式，将每个计息期末的现金流量G，2G，…，（n-2）G、（n-1）G全部折算到第n期末的将来值，求和即是等差支付的终值。

于是，图2-15中等差支付的终值为

为了求解，将上式两端同时乘以（1+i）得

F2（1+i）=G（1+i）n-1+2G（1+i）n-2+…+（n-2）G（1+i）2+（n-1）G（1+i）

将两式相减，可得

用数列求和的方法或用前面等额支付终值的公式，可以推导出上式的公式为

式（2-9）即为等差序列或梯度支付的将来值公式。上式两端同乘以（1+i）-n，则可得等差序列的现值公式为

再利用前面介绍过的等额支付终值的公式，将等差的梯度支付将来值转化为每年的等额年值。等差的梯度支付将来值F2就相当于等额支付终值公式中的F，则有

式（2-10）中的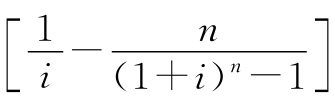称为梯度系数，通常用符号（A/G，i，n）表示。计算时既可以直接用式（2-10）计算，也可以查书后附录中的复利系数表计算。

再看图2-12，图中的将来值、等额年值和现值计算公式分别如下。

【例2-11】　王明同学2000年7月参加工作，为了买房，从当年8月1日开始每月存入银行500元，以后每月递增存款20元，连续存5年。若存款年利率为2%，问：

（1）王明同学2005年8月1日可以从银行取出多少钱？

（2）他每月平均存入银行多少钱？

（3）所有这些存款相当于王明2000年8月1日一次性存入银行多少钱？

【解】　可以将2000年8月1日看做是第一个计息期末，那么5年内的计息期为n=12×5=60，每月等差额G=20元，等差序列的固定基数A1=500元。

2000年7月1日就是第0月，即时间轴的0点。因此，现金流量图如图2-16所示。

图2-16　现金流量图

（1）王明同学2005年8月1日从银行取出的钱就是所有存款的将来值，即

（2）他每月平均存入银行的钱为

（3）所有这些存款相当于王明2000年8月1日一次性存入银行的金额为

上述等差序列公式也可以用于计算每期逐渐减少的均匀系列，只不过将公式中的G换成-G，其他项不变（推导公式略）。每期逐渐减少的均匀系列的将来值、等额年值和现值的计算式分别如下。

2）等比序列的等值计算

等比序列是指各期发生的现金流量成等比的序列。假定第1个计息期末的现金流量为A1，以后每期按百分比h递增。等比序列的现金流量图如图2-17所示。

图2-17　等比序列的现金流量图

图2-17中A1为每期的定值，h为等比系数。将每期的现金流量折算成期初的现值，然后求和，即可得等比序列现金流量的现值。

因此，等比序列现金流量的现值为

设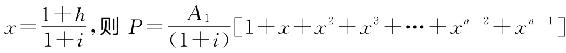，利用等比数列求和的公式可得等比序列的等值计算（calculation of equal ratio-series equivalent）公式如下。

从公式可以看出，必须令i>h，否则公式无意义。

【例2-12】　租用一套住房月租金为800元，预计今后5年内每月租金增长0.5%。若将该住宅买下，需要一次性支付10万元，但5年后仍可以卖10万元。若月折现率为1%，问：是租用合算还是购买合算？

【解】　分别计算两种情况的现值进行比较。计息期n=5×12月=60月。

若租用，5年内全部租金的现值为

若购买，则全部费用现值为

P买=100 000元－100 000（1+1%）-60元=44 955.04元

由于租金的现值小于购买的现值，因此，租用合算。

4. 补充讨论

（1）在前面的等额年值计算中，若A发生在年初，即从年初开始，情况又是如何呢？

A发生在年初的现金流量图如图2-18所示。图2-17与图2-11相比，相当于将图2-11中的A整体向前移动了一期。将各期的A逐个折算到期末，再求和，即得将来值F为

F=A（1+i）+A（1+i）2+A（1+i）3+…+A（1+i）n

图2-18　A发生在年初的等额支付图

利用等比数列求和方法可得

也可以利用A发生在期末的公式来推导。先暂时不看第0期的A，将第1期末至第n-1期末的所有A折算成第n-1期末的将来值，然后将第n-1期末的将来值再折算成第n期末的将来值，最后再用这个将来值加上第0期的A折算到第n期末的将来值。

【例2-13】　某人到银行办理了一个零存整取的业务，他每年年初存入银行5000元，若存款年利率为5%，问：他20年后可以从银行取出多少钱？

【解】　A发生在年初，则本利和为

（2）在前面的等额支付现值和等差序列现值的公式中，若n→∞，那么情况又怎样？

在等额支付现值的公式中，当n→∞时，有

在等差序列现值的公式中，当n→∞时，有

（3）若前面的资金等值计算基本公式中，计息方式采用单利而不是复利，情况又怎样呢？

与复利公式推导方法相同，可以推导单利的资金等值计算公式。

在图2-11中，各等额支付的单利将来值的和为

F=A+A（1+i）+A（1+2i）+A（1+3i）+…+A[1+（n-1）i]

经整理得

而由F=P（1+ni），所以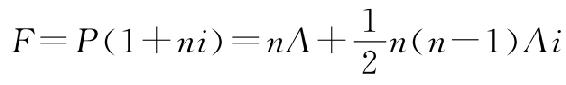，整理可得

【例2-14】　某公司发行的股票目前市场价为200元一股，每股年股息为10元，预计今后每股年收益每年增加3元。若希望达到10%的投资收益率，问：你认为目前是否可以购买该股票？

【解】　股票的寿命可以看做是n=∞，因此，该股票每股的现值为

该股票目前市场购买价为200元，低于收益，所以可以购买。

为了进一步掌握资金等值的计算和等值的概念，下面以贷款、还本利息的例子来进一步说明。

【例2-15】　张光同学向银行贷款10 000元，在5年内以年利率5%还清全部本金和利息。有以下4种还款方式。

方式一，5年后一次性还本付息，中途不做任何还款。

方式二，在5年中仅在每年年底归还利息500元，最后在第5年末将本金和利息一并归还。

方式三，将所借本金做分期均匀偿还，同时偿还到期利息，至第5年末全部还清。

方式四，将所欠本金和利息全部分摊到每年做等额偿还，即每年偿还的本金加利息相等。每种还款方式计算见表2-3。

表2-3　四种典型的等值计算
单位：元

根据表2-3中的计算方式，可以计算任何一个时刻的等值资金，如计算4种还款方式第3年末的资金等值。

方式一，第3年末的资金等值为

方式二，第3年末的资金等值为

方式三，第3年末的资金等值为

方式四，第3年末的资金等值为

从以上计算可知：任何一种还款方式在同一时刻，其资金是等值的。为了加深理解，现在再举一个实际生活中的例子。

【例2-16】　王某贷款30万元购买一套商品房，贷款20年，贷款年利率为6.5%。王某与银行约定每月等额偿还。问：王某每月应偿还银行多少钱？如果还款到第25个月时，贷款年利率上调为7%，那么从第26个月开始，王某每月又应偿还银行多少钱？

【解】　当贷款年利率为6.5%时，王某每年等额偿还银行的金额为

A年=300 000（A/P，6.5%，20）元=27 226.92元

王某还款的月利率为

王某每月等额偿还银行的金额为

A月=27 226.92（A/F，0.541 7%，12）元=2 202.10元

当还款到第25个月时，刚好还款两年零一个月。我们先计算已经偿还的本金，余下的本金按新调整的利率偿还。每年偿还情况见表2-4。

表2-4　每年偿还情况表
单位：元

下面计算第3年第1月偿还的2 202.10元中有多少是本金。

第3年末的等额欠款27 226.92元相当于第3年初的现值是：

现在再用表2-4的形式计算每月本金和利息的偿还情况，计算结果见表2-5。

表2-5　第3年每月偿还情况表（前3月）
单位：元

根据两个表的计算可知，到第25个月时已还本金和为

7 726.92元+9 496.67元+2 068.70元=19 292.29元

剩余本金为　　300 000元－19 292.29元=280 707.71元

剩余还款时间n=（12×20-25）月=215月，相当于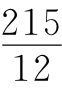年=17.916 667年。

现在贷款年利率上调为7%。王某每月还款的利率为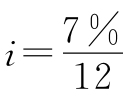=0.583 3%。

每年等额还款额为

A年=280 707.71（A/P，7%，17.916 667）元=27 972.34元

则每月等额还款额为

A月=27 972.34（A/F，0.583 3%，12）元=2 257.19元