【摘要】：在常数项级数中，有一个判别正项级数敛散性的定理——积分准则，即如果存在一单调减非负函数f：［1，＋∞）→［0，＋∞），使f（n）＝an，则正项级数与无穷积分同收敛或同发散.而级数收敛的必要条件是于是猜想收敛的必要条件也应是，但有反例如下.［反例1］ 设f（x）在［1，＋∞）上按如下定义：那么，A＞1，总可取充分大的n，使得A∈［n，n＋1），由于f（x）≥0，因此，当n→＋∞时，由夹逼性知即f（x
在常数项级数中，有一个判别正项级数敛散性的定理——积分准则，即如果存在一单调减非负函数f：［1，＋∞）→［0，＋∞），使f（n）＝an，则正项级数
与无穷积分
同收敛或同发散.而级数
收敛的必要条件是
于是猜想
收敛的必要条件也应是
，但有反例如下.
［反例1］ 设f（x）在［1，＋∞）上按如下定义：
那么，∀A＞1，总可取充分大的n，使得A∈［n，n＋1），由于f（x）≥0，因此，
当n→＋∞时，
由夹逼性知
即f（x）在［1，＋∞）上的无穷积分收敛.但f（x）是无界的，当然f（x）在［1，＋∞）上是不连续的，下面再看一个连续的函数.
［反例2］ 设f（x）在［1，＋∞）上按如下定义：
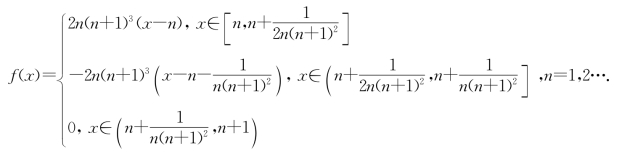
显然，这个函数在［1，＋∞）上是连续的，而且由反例1知
即
收敛于
，但f（x）也是无界的.
以上两个例子中的被积函数均在广大的无穷个区间上的函数值为零，仅在很小的无穷个区间上函数值不为零，尽管函数f（x）无界，但区间长度与函数值的乘积仍是有界的，所以，无穷积分收敛.显然，仅无穷积分收敛是推不出
或f（x）有界的.但是，如果函数f（x），在定义域内函数值不为零，且f（x）的无穷积分收敛，当x→＋∞时，f（x）就会趋向于零，弄清楚这一点，对反常积分学习是非常有益的，于是给出如下定理.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
