教会孩子用猜想的方法思考数学问题
■王洪芬
内容提要:猜想是进行数学学习和研究的一种科学方法,小学生掌握猜想的方法,可以克服对数学问题思考的盲目性,减少思维的随意性。小学数学教师要从儿童的猜想意识入手,培养他们养成猜想的习惯,学会用猜想验证的办法解决生活中的实际问题。
关键词:小学生 猜想 方法
小学生对数学的研究兴趣不在他掌握解题技巧的多少,而在于他是否掌握有主动探索问题的一些方法。经验告诉我们,一个人在数学学习上即使特别刻苦用功,只要缺乏思考问题的方法,他的学习也不会很出色。因为缺乏思考方法的人,在研究分析问题时就会漫无方向,常常采取走一步看一步的办法,存在较大的盲目性和随意性。这样导致了他们思考问题时常常抓不住问题的关键和要害,多数时候以失败告终。长期下去,就会影响他们对数学的兴趣和对数学的自信心。所以,小学教师必须教给孩子一些思考问题的方法,而不是教他们成堆的解题技巧或解题步骤。小学生常用的思考方法很多,如分析、综合、归纳、演绎、统计等,数学猜想只是其中的一种方法。
所谓数学猜想是数学学习中的一种思想方法,它是根据已知的事实和数学知识对未知量及其关系所作的合情推理。小学生的数学猜想是小学生主动探索知识的有效方法,是学生根据已有的知识经验,猜出解决问题的办法或猜出某个结果结论,然后通过实验分析或肯定或否定这个结论,猜想方法具有很明显的研究目标,清晰的研究方向,可直奔主题尽量做到在学习过程中少走弯路。孩子们能在整个活动中亲身经历亲自体验,哪怕这种猜想只有一点点的成功或者是失败,都会给孩子刻骨铭心的感受。如果猜想成功能增添孩子的自信,如果猜想失败也会带给孩子反思,便于总结教训,下一次力争做到思考全面合情推理。
当然,小学生进行数学猜想时,它的意义跟成人有着很大的区别,我们不能随意提高要求,更不能用成人的眼光看待他们的猜想。只要能够在他们的年龄、知识、经验范围内进行适当的联系、想象和猜测就不错了。孩子们到了中高年级思考富有挑战性的内容时非常适合使用猜想方法,这种方法也适用于让学生进行自主学习发现问题的时候,如像数学中的许多概念、定义、公式、法则、定律、数与数及量与量之间的关系等。猜想方法的形成与掌握要经历一个由量变到质变的长期积累过程,因此,我们必须从以下几方面着手。
一、多让孩子估计估计
要让孩子形成猜想意识,教师要从低年级起有意识加以培养。虽然低年级的小朋友的知识、经验极为不丰富,我们只要找准一切机会,让他们从“估一估、猜一猜”开始,从小就会对自己所做的事情进行估计,避免盲目模仿和机械记忆。小朋友的猜想空间是很大的。
例如,学习了加减法运算后在解决问题时,就可以让孩子先估计估计结果是多少。
问题(一):“小河里有10只鸭,又游来8只鸭,现在一共多少只鸭?”(猜一猜比10只多吗?为什么?)
问题(二):“树上有9个苹果,摘走4个后,还剩几个苹果?”(想一想比9个多吗?为什么?)
孩子们估计后就会发现,又游来8只鸭,现在肯定比原来的10只多,所以用10+8=18(只);树上9个苹果,摘了一些后肯定少了,绝对没有9个多,所以剩下9-4=5(个)。
孩子们经过这样的训练后就不会在“是用加法算呢还是减法算”举棋不定,更重要的是增强了孩子的估计能力。
二、多让孩子推测推测
孩子们到中年级,他们有了一定的估计能力,老师可提供一定的猜想情境,让他们自己展开丰富的想象,作出合情推测。
我在教学《数学》第八册《小数意义》时,先引导学生通过以具体实例认识得出,把一个整体平均分成10份、100份、1000份,其中一份或几份可以用十分之几、百分之几、千分之几表示,也可以用一位小数、两位小数、三位小数表示,说明一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几,其板书如图1所示:

图1
接下来我就让孩子们自己推测,四位小数、五位小数表示的意义呢?这时他们展开丰富联想推测到:四位小数表示万分之几,五位小数表示十万分之几……从而概括得出用来表示十分之几、百分之几、千分之几……的数叫小数。有的孩子在下面自言自语“一(十)、二(百)、三(千)、四(万)”,找到了小数位数跟分母的关系,达到了事半功倍的效果。
三、多让孩子猜想猜想
猜想是要对一个问题、结果或解决策略作出的合情推理,随着学生年龄的增加、经验的丰富、知识的积累,他们的推理能力逐渐增强,整个猜想过程日渐成熟和趋于程序化。
比如我在执教五年级长方体的体积计算时,我用棱长1厘米的正方体(体积是1立方厘米)若干个,堆成不同形状的长方体,孩子们都会用数的方法得出长方体的体积,他们也能够猜想出用分割的方法求出一个长方体的体积。此时我认为契机已到,便对他们说:“对于一个长方体形状的物体如洗衣机、电冰箱、电脑主机箱等,要想知道它的体积也是一定要用分割的方法才能求出他们的体积吗?”当然不能!因为这些物体是不能分割的,也失去了解决问题的实际意义。如果我们知道长方体的体积公式不就更好了吗?你能猜想出计算长方体的体积方法吗?于是很多同学就会从长方形的面积(S=ab)公式中受到启发,猜想出长方体的体积公式会不会是:V=abh呢?孩子们开始忙碌了,他们马上利用课前准备的材料进行研究(材料如图2所示)。
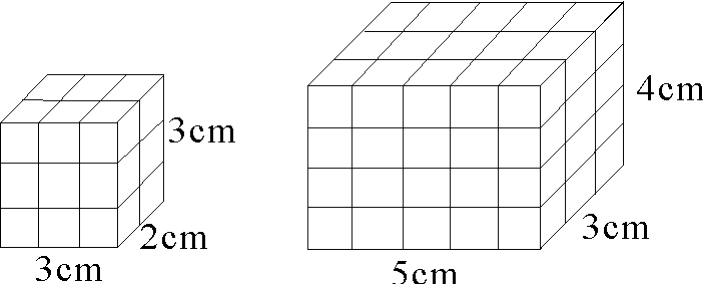
图2
(一)数:一层有3×2=6(个) 一层有5×3=15(个)
三层有6×3=18(个) 四层有15×4=60(个)
体积是18立方厘米 体积是60立方厘米
(二)算:3×2×3=18(立方厘米) 5×3×4=60(立方厘米)
他们通过自己一数一算,发现长方体的长、宽、高所含的厘米数的乘积刚好跟它体积所含的立方厘米数相等。猜想被得到证明,很多同学感到非常欣慰,而且进一步提出,正方体的体积公式为:V=a3,因为正方体是长、宽、高都相等的特殊长方体,即:正方体的体积=棱长×棱长×棱长。
长期以来,学生用数学猜想的方法思考问题的过程,我把它大致概括为以下几步。
第一步:迁移旧知,提出猜想;
第二步:大胆实践,验证猜想;
第三步:得出结论,反思猜想;
第四步:展开想象,不断猜想。
在整个高年级的学习中,如同(异)分母分数的加减计算,分数和比的基本性质,圆柱、圆锥的体积,各种平面图形的周长、面积公式,分数百分数应用题及工程问题等,都非常适合学生用猜想的方法进行思考学习和解决问题。
教学中只要我们长期坚持激励学生,他们就会自主地进行猜想不断猜想不断反思。进而使学生的数学猜想能力大大提高,特别对数学的灵感、顿悟及直觉会明显增强。
参考文献:
[1]李士琦.PME:数学教育心理[M].上海:华东师范大学出版社,2001.3
[2]数学课程标准研制组.小学数学课程标准(实验稿)[Z].北京:人民教育出版社,2004.4.
[3]成尚荣.学会数学地思维[M].南京:江苏教育出版社,2001.8.
[4]施良方.学习论[M].上海:华东师范大学出版社,2001.3.
[5]刘兼,孙晓天.数学课程标准解读(实验稿)[M].北京:人民教育出版社,2003.
(此文在第二届全国小学教师“新课程教学”论文评比中,荣获优秀论文一等奖)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

















