数项级数的收敛性

一、收敛的概念和运算性质

1．包括收敛、绝对收敛、条件收敛

2．和、差运算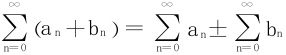

3．乘积运算：

设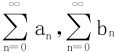是两个数项级数，称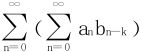为级数的柯西乘积，并有如下定理。

柯西定理　若级数都绝对收敛，其和分别为A和B。则它们各项之积a_ib_j（i，j＝0，1，2，…）按照任何顺序排列所构成的级数也绝对收敛，且其和为AB。即有

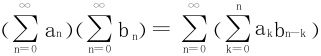
思考：当两个级数仅仅收敛时，相应结论是否仍成立？

4．数项级数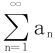收敛的必要条件：通项a_n→0

*功用：（1）判定发散级数；（2）求特殊数列的极限（通过级数收敛的判别法）。

5．项的重排

（1）∑u_n绝对收敛⇒对∑u_n可以任意重排，且和不变。

（2）∑u_n条件收敛⇒对∑u_n适当重排，其和可以变为任意其他的数，也可以得出发散级数（黎曼定理）。

二、收敛性判别法

1．Cauchy收敛准则。

2．正负部分拆：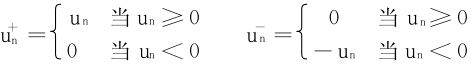

关系式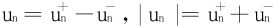，称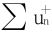为∑un的正部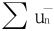，为∑u_n的负部。

结论：

逆否命题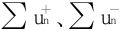中有一个收敛而另一个发散时，必有∑u_n发散。

3．正项级数的比较判别法（关键是通项无穷小量阶的分析）及其新形式。

4．正项级数的D'Alembert判别法，Cauchy根式的判别法。

稍加留意的是Cauchy根式判别法可以采用上极限形式：

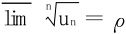
当p<1时，∑u_n收敛；p>1时，∑u_n发散。

而p＝1时，无法断定。

5．正项级数的积分判别法（转化为无穷积分）。

6．Raabe判别法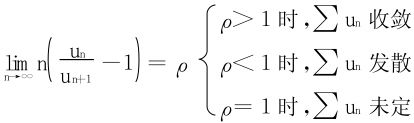　

此法是对于达朗贝尔检比法的深化。当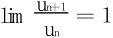时，达氏法就无法处理。须特别注意在达朗贝尔判别法和柯西根式判别法中，ρ<1时收敛，ρ>1时发散；而在拉贝判别法中，ρ>1时收敛，ρ<1时发散。刚好反了个儿。

7．交错级数的莱布尼兹判别法。

8．乘积项级数∑a_nb_n的Abel法和Dirichlet法。

9．夹逼定理，设∑a_n，∑b_n均收敛且a_n≤cn≤b_n，则∑c_n也收敛。

10．加括号去括号技巧。

对于收敛级数，其项可以任意方式加上括号，所得新级数仍收敛且和值不变。

但反之不然。何时其逆为真？

在以下两种情形，若加括号的新级数收敛，则去括号后的原级数也收敛。

情形1°　当每个括号中的项皆同号时；

情形2°　当每个括号中的项数相同或都不超过某固定值k，且通项趋于0。

关于Raabe判别法的证明思路。

引理证明：

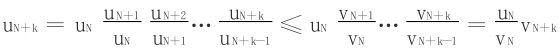
由正项级数比较判别法立得结论成立。

Raabe判别法的证明：关键在于极限条件的释放（见缝插针技术）。

如当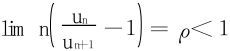时，一定∃N，以及ρ<ρ′<1，stn>N时，

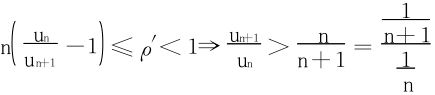
而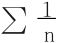发散，得知∑u_n也发散。

当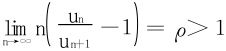时，∃N，以及1<γ<ρ，stn>N时，恒有

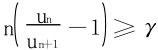
即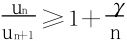仿上情形，依葫芦画瓢是行不通了，解题“手筋”何在？要在γ>1上下功夫，见缝插针。

∃　α　st　1<α<γ<ρ，且n充分大时，有

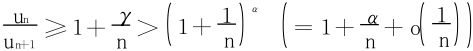
化为

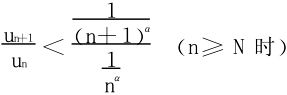
取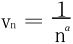，当α>1时，∑v_n显然收敛。

例1　判定下述级数的收敛性

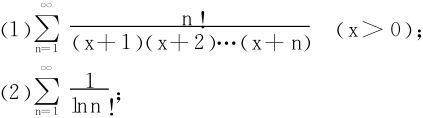
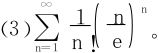
解　（1）达氏法失效，利用Raabe法

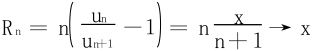
故0<x<1时，级数发散，x>1时，级数收敛；而x＝1时，代入法得知发散。

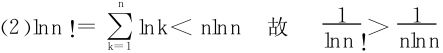
由比较法，知级数发散，或利用不等式

（3）用Cauchy根式法失效，尝试用Raabe法

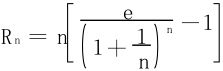
参阅第一章习题1.1第2（4）题，用洛必达法则计算出

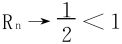
知原级数发散。

例2　研究级数的收敛性

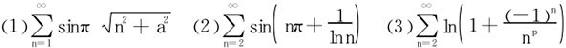
分析　这些级数都不是正项级数，且通项→0

解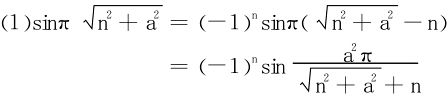　

结合Leibniz法，归结为判断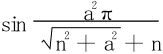的单调趋于0，此易证。

原级数条件收敛。

（2）通项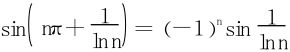，显见是条件收敛的。

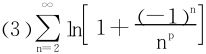
首先，该级数是一个交错级数，可先考虑何时绝对收敛，因，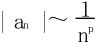

故p>1时，绝对收敛。p≤1时，用Taylor展开分析：

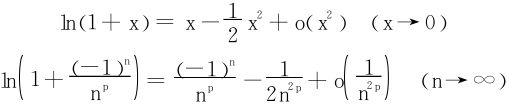
例3　讨论级数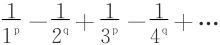的敛散性（p，q>0）

（复旦大学1982年；上海大学1999年）

解　正部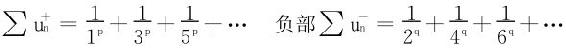

（1）p>1，q>1时，原级数绝对收敛。

（2）p>1，0<q≤1或0<p≤1，q>1时，正部、负部一个收敛一个发散，故此时原级数发散。

（条件可改写为min（p，q）≤1<max（p，q）时）

（3）0<p，q≤1时

①p＝q时，由Leibniz法知条件收敛；

②0<p<q≤1时，加括号，通项；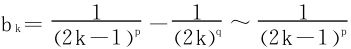

③0<q<p≤1时，加括号，通项。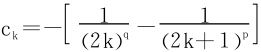

即

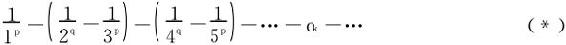
当k充分大时，由于q<p，故

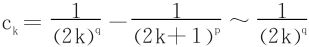
故（*）可认为是一个负项级数，适用正项级数的判定法则，知原级数发散。

例4　试证若正项级数∑a_n收敛，则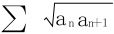也收敛，反之如何？

证明　因为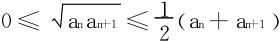，易知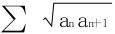收敛。或从许瓦兹不等式得证。反之不然，如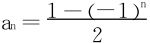。加上｛a_n｝单调不增的条件时，逆命题成立。因为此时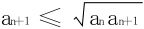，由比较判别法立得。

例5　设｛a_n｝单调递减，a_n>0，则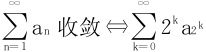收敛。

分析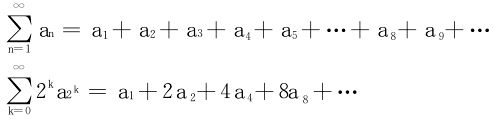　

证明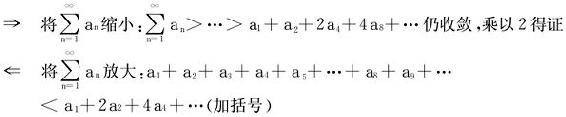　

推广：设f（x）单调下降且非负，α>1，试证：∑f（k）与∑α^kf（α^k）同敛散。

例6　设x_n为方程　xⁿ＋nx－1＝0的正根，求α的范围使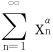收敛。

解　f（x）＝xⁿ＋nx－1，f（0）＝－1<0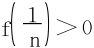，，且f′（x）>0，即f（x）严格递增。故有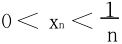

（1）当α>1时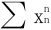，必收敛

（2）当α＝1时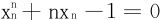，得出

　　

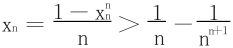
　　由比较判别法知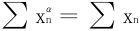必发散。

（3）当α<1时，发散。

所以当且仅当α>1时，级数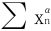收敛。

例7　设级数∑a_n（a_n>0）发散，则存在收敛于0的正数列｛b_n｝使∑a_nb_n仍发散。即：对任一个发散的正项级数，都存在一个正项级数比它发散得慢。或说没有最慢的发散级数。

分析　抽象的知识要尽可能具体化，以便于记忆或发掘证明思路。调和级数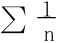是著名的发散级数，而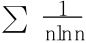则较之发散得慢，如此下去，得到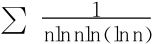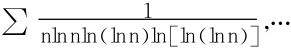，皆是发散速度越来越慢的级数。并且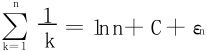（C为Euler常数，ε_n＝o（1），n→∞）

猜测b_n＝1/S_n而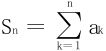为原发散级数的第n个部分和。

证明　利用Canchy收敛准则证明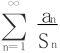发散。

分析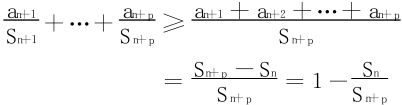　

令n定而p→＋∞，上式→1

所以　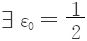，∀N ∃n₀，p₀（n₀>N，p₀≥1）st

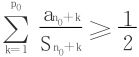
引申　注意到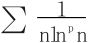，当p>1时收敛，据此推广成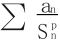：收敛（p>1）。

证明　分析积分

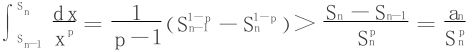
而p>1时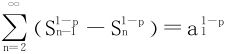，收敛（首尾相消法）。

例8　（与例7对称的结论）设级数∑a_n收敛，（a_n>0），则存在发散到＋∞的数列｛b_n｝使∑a_nb_n仍收敛。

即：对任一个收敛的正项级数，恒存在一个比其收敛得慢的级数。亦就是说，不存在收敛得最慢的级数。

注　级数收敛得快或慢可以用余和收敛于零的速度快慢来衡量和理解。

证明　令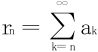为原级数的第n余项，因为∑a_n收敛，故r_n→0，取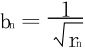，知

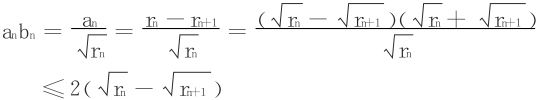
以下容易证明。

引申　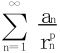当p<1时收敛，当p≥1时发散。

略证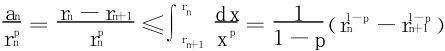　

当0<p<1时，由于r_n→0，可由首尾相消法得出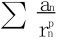收敛；

当p＝1时，要证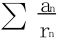发散，仍用Cauchy收敛准则

对任意正整数m，n，m<n

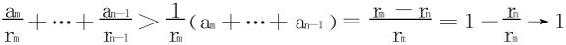（n→∞，m固定）

于是对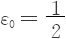，和任意m，∃n，st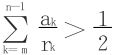

例9　设｛a_n｝是著名的裴波那契数列：1，1，2，3，5，8，…，a_n＋1＝a_n＋a_n－1；（n≥2），试分析其倒数和构成的级数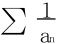的收敛性。

分析　尝试比较法，将其跟一个已知收敛的正项级数比较，等比级数显然不行，不失一般性，记b₁＝5，b₂＝8，…，b_n＋2＝b_n＋1＋b_n（即b_n＝a_n＋4）。

猜测如下结论：b₁>1×2，b₂>2×3，b₃>3×4，…，b_n>n×（n＋1）

证法一　归纳法证明上式，显然上式前四个式子都成立。设当n，n＋1时皆成立，即有

b_n>n（n＋1），b_n＋1>（n＋1）（n＋2）

则n≥3时

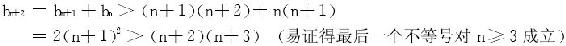
于是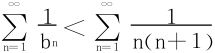右边级数首尾相消法知收敛。

证法二　显见｛a_n｝↗，a_n＋1＝a_n＋a_n－1<2a_n，据此式a_n<2a_n－1，即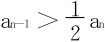，代入递推关系又得。

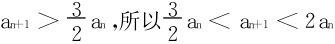变形：

依据达朗贝尔判别法

推广思考：若数列的递推式修改为a_n＋2＝λa_n＋1＋μa_n（0<λ，μ<1），是否仍有相应的结论？或者敛散性是否和λ，μ的值相关？

（浙江大学2001年，浙江省高等数学竞赛2005年（α＝1时））

解　情形1°　α>1，易见原级数绝对收敛。

　　情形2°　α＝1，原级数是

当k²≤n<（k＋1）²时，u_n同号，将符号相同的项加括号视为一个新项，得到一个与原级数敛散性相同的交错级数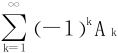，其中

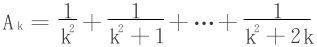
关键落实到是否有A_k单调递减趋于0？

法一　考虑单调递减函数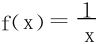在区间［n，n＋p］上的R积分，易知

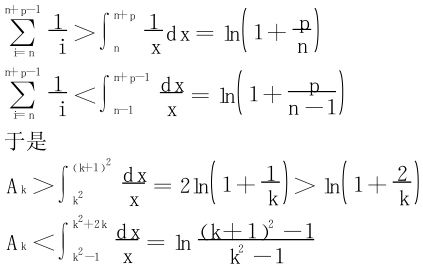
欲证A_k＋1<A_k，只需证明

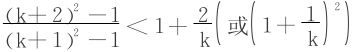，此式易验证。

这样证得｛A_k｝单调递减。由Leibniz判别法知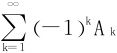收敛，从而原级数也收敛。

法二　将A_k分作两部分，A_k＝A_k′＋A_k″，其中

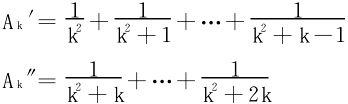
放缩法易证得

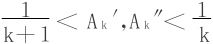
所以

用夹逼定理亦知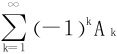收敛。

（思考：此处用于夹逼的两个级数分别是怎样的？）

法三　从（*）式又知k≥2时

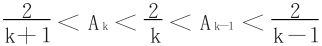
于是也证得｛A_k｝单调递减。与法一相比，此种证法更加快捷、优越。

法四　对A_k首尾两项相加大于中项的两倍：

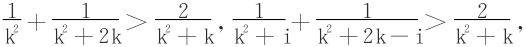
故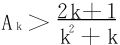，而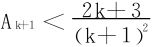易得，据此得出A_k＋1<A_k，即｛A_k｝↘。

情形3°　0<α<1

合成，稍作化简得

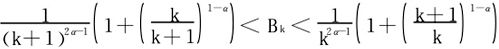
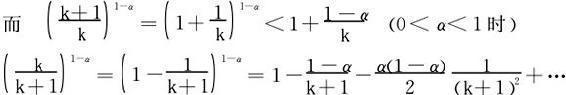
于是

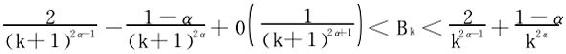
忽略掉上式左边的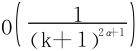项（不影响以下讨论的收敛性问题）。

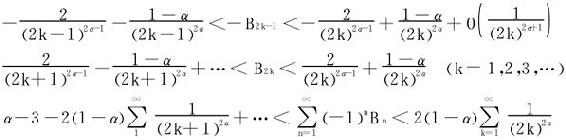
可见当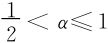时，左右两边皆收敛，原级数条件收敛；

　　当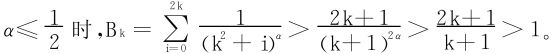　

故原级数必发散。

例11　证明级数

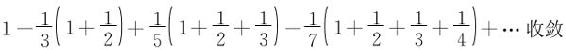
证一　级数的通项是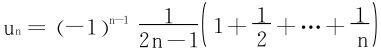

又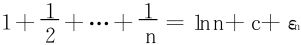，由第一章之例12，知εn↘0

原级数可以写为

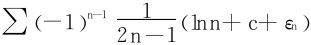
分析　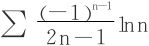，依Leibniz法，只要证出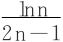单调递减趋于0，则收敛。

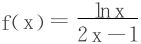（，证f′（x）<0即可）

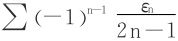，依Abel法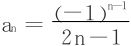，b_n＝ε_n知亦收敛，所以原级数收敛。

证二　依Leibniz判别法，只要证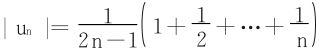单调递减（u_n→0显见）

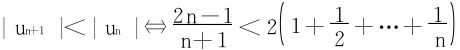，此式显然。

习题5.1

1．证明下列级数收敛：

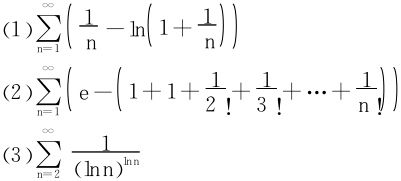
2．证明下列级数发散：

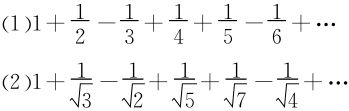
3．讨论下列级数的收敛性（p>0）：

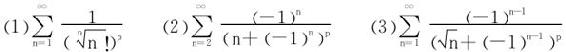
4．讨论下列级数的绝对收敛及条件收敛性：

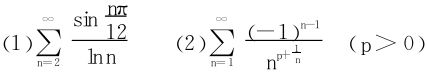
5．研究级数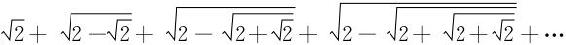的敛散性。

（中山大学2008年）

6．判定下列级数的敛散性

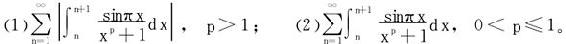
（中山大学2008年）

7．（夹逼定理）设∑a_n，∑b_n均收敛且a_n≤c_n≤b_n，则∑c_n也收敛。

8．（对数判别法）给定正项级数∑a_n，若有λ>0及n₀，使得

　　n≥n₀时有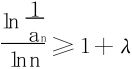，则∑a_n收敛；

　　n≥n₀时有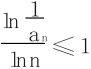，则∑a_n发散。

　　（注：请读者叙述对数判别法的极限形式）

9．正项级数∑a_n收敛的充要条件是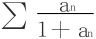收敛。

（上海师大87年）

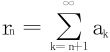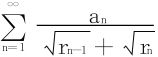10．设正项级数∑a_n收敛，余和，证明级数收敛。

11．若正项级数∑a_n收敛，且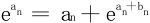（n＝1，2，…）。证明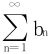收敛。

12．设x_n是方程x＝tanx的正根且依递增顺序排列，试讨论级数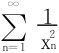的敛散性。

13．设0<x₁<π，x_n＝sinx_n－1（n＝2，3，…），证明：级数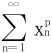当p>2时收敛；当p≤2时发散。

14．设0<p₁<p₂<…，求证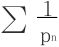收敛的充要条件为如下级数收敛：

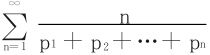
15．给定发散的正项级数∑a_n，记S_n＝a₁＋a₂＋…＋a_n，试证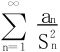收敛。

16．已知∑a_n为一般项发散级数，证明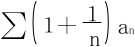也发散。

（华东师大98年）

17．设a_n≠0（n＝1，2，…）且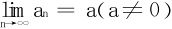。求证：下列两级数

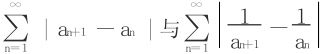
　　同时收敛或同时发散。

18．设级数∑a_n收敛，∑（b_n＋1－b_n）绝对收敛，试证级数∑a_nb_n也收敛。

19．设｛na_n｝收敛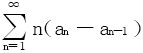收敛，则∑a_n收敛。

20．如果级数∑a_n的所有子级数都收敛，则∑a_n绝对收敛。

21．设a_n>0（n＝1，2，…），证明级数∑a_n收敛的充分必要条件是连乘积数列｛（1＋a₁）（1＋a₂）…（1＋a_n）｝收敛。

22．如果u_n是正的单调递增数列，则级数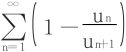当u_n有界时收敛，而当u_n无界时发散。

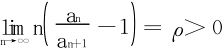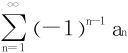23．设a_n>0，且，则级数收敛。

24．若正项级数∑a_n收敛且｛a_n｝单调减少，则有。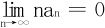

25．若正项级数∑a_n收敛且｛na_n｝单调减少，则有。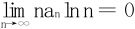

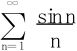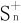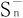26．给定级数。将其前n项部分和S_n分成正部和负部的差，即

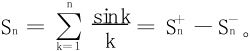
　　证明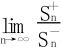存在并求其值。

　　并思考：对一般条件收敛级数是否有相应结论？

27．假设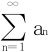发散，且｛a_n｝是正的递减数列，试证：

28．若∀数列｛x_n｝，只要x_n→0（n→∞），就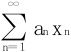有收敛，则有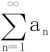绝对收敛。

29．按以下要求分别构造出相应级数∑a_n。

　（1）∑a_n收敛但；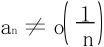

　（2）∑a_n收敛，但∑a_nlnn发散；

　（3）∑a_n收敛，b_n～a_n（n→∞）但∑b_n却发散。

30．证明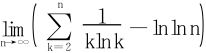存在。

31．试证：弃掉调和级数

　

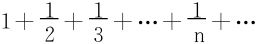
　中分母含有数字9的项（如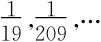），所得级数收敛。

（浙江大学1999年）