从《九章算术》到《缉古算经》

中国古代数值解方程的方法是与开方方法连在一起的。事实上，在中国传统数学中，开方法（即求）与高次方程（即）数值解法被统称为开方术。因为后者正是在对开平方、开立方方法的基础上不断改进和发展而取得的。因此，在这一节我们就从最简单的开平方术开始来介绍一下古代中国的开方术。

开平方的完整程序被记载在中国古代最重要的数学著作《九章算术》“少广章”中。对这本名著的介绍我们放在下一编，这里我们所要做的是以书中“少广章”第12题为例说明一下开平方的方法。

这一题目是：“今有积五万五千二百二十五步。问为方几何？”意思是说，已知面积55225步，问作为正方形其边长为多少？“答曰：二百三十五步。”

为求解这一问题，在几个类似的题目之后，书中给出了开方术：“置积为实。借一算，步之，超一等。议所得，以一乘所借一算为法，而以除。除已，倍法为定法。其复除，折法而下。复置借算，步之如初。以复议一乘之。所得副以加定法，以除。以所得副从定法。复除折下如前。”

这一术文所表达的是古代用筹算演算开平方的步骤。

所谓筹算，就是用“算筹”作为工具来计算和演算的方法。算筹是一种竹制的短棍，后来也用木制、玉制等。至迟在春秋战国时期，算筹已得到普遍的应用，而且人们已经可以熟练地运用它来进行计算了。比如《老子》书中就有“善数者不用筹策”的话。

筹算记数法使用十进位值制，并有纵横两式。如下图所示，第一行为纵式，第二行为横式。可以看到，对5或小于5的数字，几根算筹就表示几；对数字6、7、8、9，则其中有一根筹，以一当五。

那么如何用算筹记数呢？对此现存的最早记载来自《孙子算经》：“凡算之法，先识其位。一纵十横，百立千僵，千十相望，万百相当。”前两句说明数位在记数中的重要意义，后四句则给出了用纵横两式记数时的规则。其中规定个位用纵式，十位用横式，百位用纵式，千位再用横式……以此类推，交替使用纵横两式。这样顺着个、十、百、千……的次序，从右向左，数码纵横相间，遇到零时空位，由此就可以表示出任意一个数目。例如2561可摆成。

在十进位制算筹记数法基础上，中国古代建立了算筹的加减乘除四则运算，进而还可以利用算筹进行开方以及其他的代数计算。下面我们就来结合算筹演算图看一下中国古代是如何利用算筹对前面的题目开方的。

如图（1）所示，筹式排成四列。“实”指被开方数，此处是55225；下隔一行置一算筹于个位称为“借算”。将“借算”向左移动，移动一位称为“步”，隔一位一“步”称为“超一等”。这样一直移至不可再“超”时为止。在本例中，借算经两次“超一等”可移至万位上，移动后的“借算”表示10000。于是得到图（2）中的筹式。至此，所进行的步骤就是开方术所称的：“置积为实。借一算，步之，超一等。”然后，考虑到被开方数是55225，其开方后的结果一定是三位数，下面就先确定所得方根百位上的数字。由于2002<55225<3002，所以百位数字可以确定为“2”。将议得的结果置于商的百位。于是得到图式（3）。

上面3个图中都使用了算筹数字，这是为了让读者更好地体会古代演算的方式。为了方便，在下面的介绍中，我们将把图示中的算筹数字换为阿拉伯数字。比如上面的3个图可以换为下面的对应图示。

继续我们的介绍。

在百位上“议得”方根第一位数字为2后，将此数乘以“借算”得“法”：2×10000=20000；以下在“实”这一行中做减法运算：55225-2×20000=15225。如下图（4）、图（5）所示。至此，所进行的步骤就是开方术中所说的“议所得，以一乘所借一算为法而以除（除即减）。”

然后将“法”乘以2（第一次倍法）为“定法”，即20000×2=40000为定法。此即谓“除已，倍法为定法。”再下面的步骤就与上面的大体类似了。“其复除，折法而下。复置借算，步之如初。”即先按照步骤（1）中的方法重新确定“借算的位置”，“步得”100。同时定法退一位成：40000÷10=4000。得到如下图（6）所示

在十位上“复议”得方根的第二位数字3（可通过实15225除以法4000而估得），将此数乘以“借算”为“所得”：3×100=300，暂置于“定法”之下称为“副”；又将“所得”加到“定法”4000上得4300；在“实”这一行中进行减法运算，有：15225-3×4300=2325。如下图（7）、图（8）所示。此即谓“以复议一乘之。所得副，以加定法，以除。”

再把“所得”300加到新的“定法”4300上，得4600（第二次倍法）。然后按照与上面类似的方法将“定法”退一位成460，并且重新确定“借算的位置”，此时“借算”置于个数表示1。最后在个位上“议得”方根第三位数字为5，然后依照前面的步骤最终在“实”这一行中有：2325-5×465=0，表示开方已尽，方根为235。如下图（9）～图（13）所示。此即谓“以所得副从定法。复除折下如前。”在开方术中省略了“以复议一乘之，所得副以加定法，以除”的话。

为做对照，我们再介绍一下用现代笔算对55225开平方。其步骤来自20世纪30～50年代的中学教科书，括号内是与之对应的开方术中的步骤。

（1）将要开方的数从个位起向右每二位分为一节。（置积为实，借一算，步之，超一等）

（2）最左一节是5，而22=4，32=9，故知5的方根的整数部分是2。（议所得）

（3）从5减去22=4，余1，加入第二段得152。（以一乘所借一算为法，而以除）

（4）用2乘20得40。（除已，倍法为定法。其复除：折法而下。复置借算，步之如初）

（5）用40除152，得商3。将3加于40，得43。（以复议一乘之。所得副以加定法）

（6）从152减去43×3=129，余23，加入第三段，得2325。（以除）

（7）用20乘43，得460（以所得副从定法。复除，折下如前）

（8）从460除2325，得商5。将5加于460，得465；从2325减去235×5=2325，无余数，故所求平方根为235。（以复议一乘之，所得副以加定法，以除）

由此可见，现代的笔算开方与古代的开平方术两者思路相当一致，在各个主要步骤上可以说是若符若节。当然，在具体操作上，现代人可能会觉得古代的方法要烦琐一些。但对熟悉筹算的人来说，按这种程序实际摆筹运算其实是相当简便的。

问题是，这种开方程序为什么是合理的？后来魏晋时期的数学家刘徽在《九章算术注》中从几何角度解释了这种开方程序的正确性。

刘徽首先指出，开平方从几何上看，相当于由正方形的面积推求其边长。于是，开平方术可以借助于平面图形的分割来理解。

如下“开方图”所示，给定“实”55225，相当于知道正方形AD的面积是55225。设√55225=a+b+c，其中a为百位数，b为十位数，c为个位数。

首先，确定正方形AB边长a=200。由此知，此正方形的面积是2002。从正方形AD中减去它，得“曲尺形”EDHGBFE的面积为：55225-2002=15225。

现在看这个大曲尺形中包含的一个小曲尺形ICKGBFI的面积。容易知道，若把此小曲尺形拉直，则它可看做宽为b（即图中GK或FI），长为2a+b的一个矩形，其面积为（2a+b）b。议得b=30，则其面积为（2×200+30）×30。

在大的曲尺形EDHGBFE中减去这一个小的曲尺形ICKG-BFI，可得到15225-（2×200+30）×30。这就从几何意义上基本解释了开平方术中的做法由来：取2000×2=4000为法；取100×3=300为“副”；“所得副，以加定法”，即取4000+300=4300；“以除”，15225-4300×3=2325。整个筹算过程相当于是计算15225-（2×2000+300）×3。可以看到筹算开方术与这里的几何意义有一点小差别，原因在于前者的b取十位数上的数字3，而后者b取十位数30。

至此，剩下一个更小的曲尺形EDHKCIE。同样的道理，它可看做宽为c，长为2（a+b）+c的一个矩形，其面积为[2（a+b）+c]c。议得c=5，则其面积为（2×230+5）×5。在这一步后，剩余面积2325-（460+5）×5=0，因此得方根为235。

由此可见，中国古代开平方的几何概念非常清晰：它是将方幂分割为一个正方形和若干曲尺形，其宽度恰好表示方幂一边长度在各“位”上的数值（如此例中的200、30、5）。方幂先减去这个正方形，得到一个大的曲尺形。然后每次减去一个曲尺形……这一过程持续下去，剩余的面积越来越小，直到为零为止，开方也就完成了。

如果用现代的代数语言来解释开平方的原理，就更容易理解了。

如果被开方数是两位数，即设√N=a+b，则（a+b）2=a2+2ab+b2=a2+（2a+b）b，在确定了初商a后，得到剩余（a+b）2-a2=N-a2=（2a+b）b。利用这一关系可确定次商b：为此先“倍法”得2a，而后由（N-a2）/2a即可估得第二位数b。然后在剩余的面积N-a2基础上减去（2a+b）b，即N-a2-（2a+b）b=N-（a+b）2=0。余数为0，开方结束。

如果被开方数是三位数，即设√N=a+b+c，则（a+b+c）2=a 2+2a（b+c）+（b+c）2=a2+（2a+b+c）（b+c），在确定了初商a后，得到剩余（a+b+c）2-a2=N-a2。为确定次商b，先第一次“倍法”得2a。由（N-a2）/2a估得第二位数b，然后在剩余的面积N-a2基础上减去（2a+b）b，即N-a2-（2a+b）b=N-（a+b）2。为了继续确定商c，第二次“倍法”得（2a+b）+b=2（a+b），由（N-（a+b）2）/2（a+b）估得第三位数c。在得到c之后，再由前面的剩余部分减去[2（a+b）+c]c，即N-（a+b）2-[2（a+b）+c]c=N-（a+b+c）2=0。余数为0，开方结束。

显然，这样的思路可以应用于被开方数是更多位的情况。因此，从代数学角度而言，筹算开平方法运算过程的实质与理论依据是完全平方公式（a+b）2=a2+2ab+b2，或者说是应用了二项展开式系数中的1、2、1。

至此，我们详细介绍了《九章算术》中的开平方术，并从几何角度与现代的代数角度解释了开平方术的原理。除此外，我们还可以把开平方术与二次方程求解联系起来，从方程的角度来理解一下开平方术。

非常显然，对一个正数开平方从方程的角度考虑就相当于求缺一次项二次方程x2=A的根。如上面的55225开方，相当于求解方程x2=55225。于是，对上面介绍的开平方术，也可以从方程的角度做一下现代解释。

首先可以注意到，开平方的筹算图最下层的借一算，它一方面可以作定位之用，另一方面也可以看做是最高项x2的系数；而每一个筹式，由下而上，正好可以看做是一个二次方程各项系数。正因此，开平方一方面可以看做是算术运算，另一方面也可以看做是二次方程的一般解法。事实上，中国古代数学中关于方程的解法，正是由开方法演变而来。下面我们就以55225开方为例，来分析一下开平方的各个演算步骤是如何与求缺一次项二次方程的正根过程相对应的。

第一步“超”，相当于对原方程做了一个缩根变换。若移动n次，则变换后的新方程为。以x2=55225为例。“借算”向左移动，每一次移二位，移二次后停住，这一步骤相当于对原方程做了一个变换x=102x1，则变换后得到的新方程为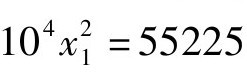[这一方程对应于上面筹算图（2）]。之所以如此做，是为了在变换后求得第一位商，即百位数字x1。

第二步是“议”。显然，对55225开平方中议首商相当于确定新方程的整数部分。易知[x1]=2。

第三步“除”，相当于对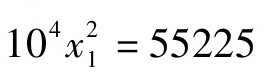做了一个减根变换，即令x2=x1-2。于是用我们现代的做法可以直接得到一个新方程104（x2+2）2=55225，整理即得

第四步“折”。为此在开方术中重新布置算筹，使借算超一等（在后来的改进中，算筹不再重布，而是直接退两位），法退一位。这相当于对上面的方程做了一个倍根变换。即令x3=10x2。于是得到变换后的方程为：[这一方程对应于上面筹算图（6）]。

然后重复以上4个步骤：先议得方根的第二位数为3。然后做一个减根变换：x4=x3-3，得到新方程100（x4+3）2+4000（x4+3）=15225，整理[这一方程对应于上面筹算图（9）]。

然后继续重复做一个扩根变换x5=10x4，于是得到变换后的方程为[这一方程对应于上面筹算图（10）]。再议得第三位数为5，代入恰好满足方程。于是x5=5，一步步代回去，可得到x=200+30+5=235。

因此，从现代意义上讲，开平方术解x2=A的整个过程包括四类算法：缩根，目的是使方根缩小至原来的1/10n（n是算筹移动的次数）而仅保留一位整数；估根，目的是通过试除确定这个整数的数值；减根，目的是除去这个已经确定的整数；倍根，目的是使方根剩余的部分扩大至10倍而重现一位整数。重复以上步骤，就可逐一求出方程x2=A的正根的各位数字，从而得到方程的正根。

如果二次方程含有一次项呢？古代中国把一次项系数称为“从法”，常数项称为“实”。因此把形如x2+px=q的含一次项的二次方程的解法叫做“开带从平方”。

《九章算术》没有给出开带从平方的程序，然而稍加观察即可以注意到开方术从求根的第二位得数起，便是求形如x2+px=q的方程的正根的程序。比如在上面所介绍的55225开平方过程中，议平方根的第二位和第三位数字时，所列的算式[开方筹算图中的图（6）与图（10）]便是有“从法”的开方式，相当于解含有一次项的二次方程：100x2+4000x=15225（或做缩根变换后得到的y2+400y=15225）以及x2+460x=2325。

由此可见，《九章算术》开平方术已经包含了开带从平方的程序。也就是说，开带从平方可由一般的开平方的方法直接导出。这意味着，开平方术可以推广到解一般的正系数二次方程。在《九章算术》中还出现了这样的实例：《九章算术》第九章勾股章第20题，最后可化为求解二次方程x2+34x=71000。关于解法术文说：开方除之……。这是后世所谓开带从平方的首例。

我们说明一下其求解办法。先摆放算筹如图（1）所示。由71000为五位数，可确定所求解为三位数。下面我们按“超”、“议”、“除”、“折”四步走。

第一步是“超”：借算向左移动四位，法向左移动两位。如图（2）所示。与之对应的是做缩根变换x=100x1得到方程。

第二步是“议”，由2002<71000<3002，所以百位数字可以确定为2。将议得的结果置于商的百位。于是得到图式（3）。

第三步是“除”，开带从平方这一步与开平方稍有不同的是，在每求出一位得数之后，要多减去一个34与相应商数的乘积。如在求得第一位得数2后，除减去2002外，还需要减去34×200，即71000-2002-34×200=24200。如图（5）所示。与之对应的是，做减根变换x2=x1-2并得到方程。

第四步是“折”，借算退两位，法退一位。如图（6）所示。与之对应的是，做扩根变换x3=10x2得到方程。

然后重复以上4个步骤：先议得第二位数为5，将此数乘以“借算”为“所得”：5×100=500，暂置于“定法”之下称为“副”；又将“所得”加到“定法”4340上得4840；在“实”这一行中做减法，有：24200-4840×5=0，余数为0，运算结束。可以注意到，这一步在求得第二位得数5后，减去的是（2×200+50+34）×50。这是因为在开带从平方时，每求得一次商时，总要把“从法”（34）加入之后再乘而后相减。如下图（7）、图（8）所示。这相当于做了一个减根变换x4=x3-5后得到方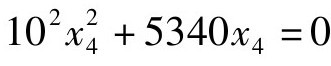。由此最后一位数字为0。所以原方程的一个正根为250。

在《九章算术》中除开平方问题及开平方术外，还有四道开立方的题目，并在题目后给出了开立方术：“置积为实。借一算步之，超二等。议所得，以再乘所借一算为法而除之。除已，三之为定法。复除，折而下。以三乘所得数置中行。复借一算置下行。步之，中超一，下超二等。复置议，以一乘中，再乘下，皆副以加定法。以定法除。除已，倍下，并中从定法。复除，折下如前。”

由于开立方的筹算操作更为复杂，我们不再做介绍。我们下面只给出几点结论。

首先，对比开平方术和开立方术，不难看到，两者开方的程序基本是一致的。它们都是通过筹式布算，机械重复实施“超”、“议”、“除”、“折”几个步骤，直到适尽，结束。差别在于，开立方中筹式布算要多增加一行“中行”，使原来的四行布算变为五行布算。另外在“超”、“折”的步骤中有小的变动或调整。如在开平方中，是“超一等”，而在开立方中，是“超二等”（即移动算筹时隔两位一“步”）。

其次，刘徽对开立方术也给出了几何解释：开立方可以看做是由立方体的体积求棱长，而开立方的过程可从立方体的分割角度做出理解。

再次，《九章算术》中的开立方术同样可从现在代数角度理解。

如果被开方数是两位数，即设，则（a+b）3=a3+3a2b+3ab2+b3=a3+（3a2+3ab+b2）b，在确定了初商a后，得到剩余（a+b）3-a3=N-a3=（3a2+3ab+b2）b。在确定次商b后，又有N-a3-（3a2+3ab+b2）b=0。如果被开方数是三位数……可以做类推。因此，从代数学角度而言，筹算开立方术的运算过程其实质与理论依据是完全立方公式（a+b）3=a3+3a2b+3ab2+b3，或者说是应用了二项展开式系数中的1、3、3、1。

此外，开立方可以看做是解方程x3=A。而从方程变换的角度分析也可理解导致筹算中“超”、“折”调整的原因。比如要对1860867开立方，即求解x3=1860867。易知根是一个三位数。为了得到第一位根值，可做一个变换x=100x 1，于是得到变换后的方程，（100x1）3=1860867，即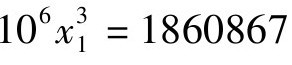，这表现在筹算中就是超二等。

另外，与开平方情况类似，在开立方的过程中也包含了开带从立方。这意味着，开立方术可以推广到解一般的正系数三次方程。不过，在《九章算术》中没有出现开带从立方的问题。

刘徽生活于魏晋时期，中国古代著名数学家，其数学研究多有创见。这里先介绍一下他在开方术方面的几点工作。

在开方术方面，刘徽首先给出了开平方术、开立方术的几何解释，从而说明了《九章算术》开方术程序的合理性，使人们对开方术有了直观性的感性认识。同时，刘徽还对开方程序做了改进。在《九章算术》开方术中，借算在每使用一次后都要撤去，议得次一位得数时要重置借算于个位，然后再“步之如初”，这显得烦琐。刘徽的做法是保留借算，直接将其退位（在开平方时每求得一个商后，退两位；在开立方时每求得一个商后，退三位），这样显得更简洁，而且使开方程序具有连续性。刘徽之后如《孙子算经》等著作中都接受、使用了刘徽的这一改进做法。

刘徽更重要的一项工作是在开方中提出求微数的思想。我们上面所举的例子，被开方数是正整数，开方步骤都在进行到个位数数字或之前结束，于是开方后得到的结果也都是正整数。但如果开方得到个位数字后，余数仍不为零时如何处理呢？这种开方不尽的情形，相当于求无理根。在《九章算术》的各个问题中没有出现这种情况，因此没有对此做探讨。刘徽则对此给出了漂亮的处理方法。

他指出，在遇到开方不尽时，为得到精确近似值，要在求出整数部分之后，“加定法如前，求其微数。微数无名者以为分子，其一退以十为母，其再退以百为母。退之弥下，其分弥细，则朱幂虽有所弃之数，不足言之也。”也就是说，可以继续开方程序以“求其微数”，即求无理根的十进分数（相当于现在的十进小数），用这种十进分数逼近不尽根，直到得到比较满意的近似值为止。刘徽的求微数思想进一步完善了《九章算术》的开方术，同时这一思想还开创了十进小数的先河，对中国在宋、金时代最先使用小数起了促进作用。

在《九章算术》及刘徽之后，南北朝时期的数学家祖冲之在开方术方面可能又取得了一些重要进展。然而，十分可惜的是，记录其研究成果的《缀术》一书，“学官莫能究其深奥，是故废而不理”，最终失传了。只在《隋书·律历志》中，在叙述了祖冲之圆周率方面的成就后又记载道：“又设开差幂、开差立，兼以正负参之。指要精密，算氏之最者也。”据这种极其简略的记录，后人认为祖冲之可能研究了含有负系数的二次与三次方程求正根问题，并提出了具体方法，谓之“开差幂”、“开差立”。这种方法，可能类似于后来北宋数学家刘益提出的“正负开方术”。

再之后的进展由初唐数学家王孝通做出。王孝通的研究结果记载在其传世著作《缉古算经》（约626年）中。《缉古算经》是一本实用问题集，主要涉及天文历法、土木工程、仓房和地窖大小以及勾股问题等。王孝通出色的工作，首先体现在其依据实际问题立高次方程方面。在古代，没有现代的符号代数，要由实际问题立出开方式（即高次方程）并非易事。王孝通是通过几何方法，以文字形式建立方程的。在每一条有关高次方程的术文之下，他都用自注来说明方程的各项系数（实、方、廉、隅）的来历。最终，王孝通在不用数学符号的情况下列出了28个三次方程，这不仅解决了当时的社会需要，也为后来天元术的建立打下了基础，成为后来“天元术”的重要先声。

王孝通从实际问题出发得到的三次方程，用现在的符号可统一表示为：x3+px2+qx=r，（p>0，q≥0，r>0）。简单地说，就是正系数的三次方程。书中对这些方程如何求解没有给出演算程序，而只是用术文简述其解法为：“以r为实，以q为方法，以p为廉法，从开立方除之，即得x。”这里的所谓开立方除之，即是开带从立方法。可以确信，王孝通的解法是由《九章算术》少广章的“开立方术”推广而来。具体来说，就是用《九章算术》开立方法中求方根第二位及以后各位的方法来求三次方程正根。经验证，其解答都是正确的。可见王孝通当时已掌握了三次方程的数值解法，这在世界上是领先的。从数学史上而言，王孝通最早提出了三次方程代数解法（开带从立方），其《缉古算经》一书也成为关于三次方程数值解法及其应用的最古老的文献。

从《九章算术》少广章提出完整的开平方、开立方程序，其后经过刘徽、祖冲之和王孝通的工作，到7世纪时，中国古代数学家已经圆满地解决了正系数二次、三次方程求正根的问题。