有关证明分析法之发现的障碍

4.有关证明分析法之发现的障碍

现在让我们回到主要问题上来。为何从1821年到1847年，主要的数学家都没有发现柯西证明的简单的缺陷并改进证明分析和定理呢？

首先想到的回答是，他们不了解多证多驳法。他们不知道在发现一个反例之后必须仔细分析其证明并尝试找到过错引理。他们处理全局反例是借助于探试性的且没有创造力的例外排除法。

实际上，赛德尔一下子就发现了证明生成的一致收敛概念和多证多驳法。他完全意识到了他的方法论上的发现^[26]，他在其论文中非常清晰地叙述道：

从刚才达到的确定性可知，定理不是普遍有效的，因此其证明必然要依赖一些附加的隐含假设，那么，主题的证明则有赖于更详细地分析。发现隐藏的假设并不是非常困难。于是，人们可以逆推这一由假设所表达的条件不能被表示非连续函数的级数所满足，因为只有如此，在其他正确的证明序列与另一方面已经确证的证明序列之间的一致性才能重新恢复^[27]。

是什么阻碍了赛德尔之前的一代人发现这一点呢？主要原因（我们已经提到过）是欧几里得方法论的流行。柯西的严格性的革命是由于有意识地试图把欧几里得方法论应用到微积分学中而引发的^[28]。他以及他的追随者认为，正是由于这一点，他们可以带来光亮以消除“分析的巨大黑暗”^[29]。柯西是在帕斯卡准则精神之下前行的：他首先依照算术中非常熟悉的术语，着手定义分析中含糊不清的术语，像极限、收敛、连续性等等，然后，他继续证明以往没有被证明或不是非常明显的所有东西。既然在欧几里得的框架下，并没有尝试证明什么是错误的东西的先例，所以柯西首先必须通过丢弃错误的垃圾来改进数学猜想的主体。为了改进猜想，他运用了留心例外、把先前轻率表述的猜想限制在有效的范围之内而使之处于安全地带的方法，即，他运用了例外排除法^[30]。

一位作者（可能是卡塔兰（Catalan））在《拉罗斯大百科全书》1865年的版本中相当具有讽刺意味地刻画了柯西对反例的寻找。他写道：

他带入到科学之中的只是些消极的学说……事实上，他所发现并小心使其清楚明白的几乎总是真理消极的一面：如果他在白粉中发现了一些金子，他将向世界宣称，粉笔并非单独地由石灰做成。

阿贝尔写给霍尔姆博的信中有一段内容是这种柯西学派新的内心反省倾向的进一步例证：

我已经开始从这一方面检查（目前）我们通常会认可的那些最重要的规则，并且说明它们在何种情况下是不适当的。这一工作进展顺利，给我带来了无限的乐趣^[31]。

被要求严格性的人（rigourist）当作是无用的垃圾的东西，比如关于发散级数和的猜想，当然都会被付之一炬^[32]。“发散级数是”，阿贝尔写道，“恶魔的作品”。它们只会引起“灾难和悖论”^[33]。

但是，当坚持不懈地努力用例外排除法改进其猜想时，他们却从没想到用证明来改进猜想。在欧几里得的传统中，猜测和证明两种活动是被严格分开的。名副其实的且依然不是最终确定的证明的观念与要求严格性的人是背道而驰的。反例往往被看作是错误的和灾难性的缺陷它们表明一个猜想是错误的，并且就不得不再次从头开始证明。

鉴于这一事实，就可以理解，为什么在18世纪一些乱七八糟的归纳推理都被叫做证明了^[34]。但是，也没有办法来改进这些“证明”他们被正当地抛弃，因为“不严格的证明——那就意味着，根本就不是证明”^[35]。归纳论证是容易出错的——因此要付之一炬。演绎论证取而代之——因为它始终不会出错。“我让所有不确定性消失了”，柯西这样宣称^[36]。正是基于这样的背景，对柯西的“严格地”证明了的定理的反驳必须被重视。这一反驳不是孤立的事件。柯西关于欧拉公式的严格证明，正如我们所看到的，随后照样有一些论文陈述了大家熟知的“例外情况”。

只有两条出路：或是修正欧拉方法所基于的全部绝无谬误论者（infallibilist）的数学哲学的基础，或是以某种方式隐瞒问题。首先让我们来看看，修正绝无谬误主义者的方法包括哪些内容。毫无疑问，必须放弃全部数学可以还原为毋庸置疑的真实细节以及存在对某些表述的真实性直觉不可能犯错误的想法，也必须放弃我们的演绎、推理的直觉是不可能错误的想法。只有承认这两点，才能打开多证多驳法自由发展的路径，使其应用到演绎论证的关键性评价中去并用来处理反例问题^[37]。

只要反例依然不但是定理的缺陷，而且也是鼓吹它的数学家的缺陷；只要还认为要么是证明要么是非证明，不存在带有缺点的合理的证明；那么，数学中的批评就还是被禁止的。正是绝无谬误主义者的欧几里得方法的哲学背景滋养了数学中权威性的传统模式，阻碍了猜想的公布和讨论，使数学批评不可能兴起。文学批评可以存在是因为我们可以欣赏一首诗而不认为它是完美的；只要我们仅仅只欣赏产生完美真理的数学和科学的结论，数学或者科学的批评就不可能存在。一个证明之所以是一个证明只要它是在证明；它或者证明出或者没有证明出。这一观念——被赛德尔表述得如此清晰——就是一个证明之受到尊敬并非是没有缺陷，这在1847年是革命性的，并且，不幸的是，今天听起来依然是革命性的。

并非是巧合，多证多驳法出现于19世纪40年代，此时正当牛顿光学崩溃（通过菲涅耳（Fresnel）18世纪10年代至20年代的工作）以及非欧几何的发现（由罗巴契夫斯基（Lobatschewsky）在1829年和波尔约（Bolyai）在1832年）粉碎了绝无谬误论者的狂妄幻想的时期^[38]。

在多证多驳法发现之前，“严格证明了的”定理由于连续不断的反例而引起的问题仅能够通过例外排除法来解决。证明证明了定理，但是却留下了何为定理的有效范围的问题。我们可以通过规定和小心地排除“例外”（这一委婉的说法是那个时期的特征）来决定这一范围。这些例外于是就写入定理的表达之中。

例外排除法的支配地位表明欧几里得方法，在某些至关紧要的困难情境中，对数学的发展起到了有害的效果。这些困难情景绝大部分出现在正在发展的数学理论之中，在那里，正在形成的概念是进步的运载工具，诸多激动人心的发展来源于通过拉伸概念、区分先前没有被区分的概念所进行的对概念范围的边界的探索。在这些发展的理论中，直觉是没有经验的，它跌跌撞撞还会出错。没有理论不经过这样一个发展阶段；而且，这一阶段从历史学家的眼光来看是最激动人心的，从教学的角度来看也应该是最重要的。如果不理解多证多驳法，如果不接纳难免有错误论者（fallibilist）的方法，就不能真正地理解这些阶段。

这就是为什么欧几里得，特别是对于数学史和数学教学来说，不管是在初级还是在创新层面，一直都是邪恶的天才的原因^[39]。

按语：在这一附录中，多证多驳法的5、6、7这些补充的阶段并没有被讨论。我在这里只是提一下，有条不紊地搜寻其他的证明中（阶段5）的一致收敛很快就会产生对柯西所证明的另一个定理的反驳和改进：这一定理就是，任意连续函数的收敛级数的极限的积分是各项积分序列的极限，或者简言之，就是在连续函数的级数的情况下，极限运算和积分运算可以相互交换。这在整个18世纪都是毫无争议的，甚至高斯都不假思索地加以运用了。（见高斯［1813］，克诺普（Knopp）［1928］和贝尔［1945］。）

赛德尔，他在1847年发现了一致收敛，现在却没有去看看在别的证明那里是否暗中假定了这一概念。斯托克斯，他在同一年发现了一致收敛——虽然不是借助于多证多驳法——却在同一篇论文中使用了关于级数积分的错误的定理，参阅莫格诺（斯托克斯［1848］）（斯托克斯还犯了另一个错误：他认为他已经证明了一致收敛对于极限函数的连续性不仅是充分的而且是必要的。）

关于级数的积分也依赖于一致收敛的假设的证明之推迟，也许是因为这一原始猜想只是在1875年才被一个具体的反例所驳倒这一事实（达布［1875］），那时，已经通过证明分析在证明中追踪一致收敛了，但却没有反例来促成这种分析。对一致收敛的搜寻一旦完全由维尔斯特拉斯来领导，很快就在有关逐项微分、二重极限等的证明中发现了这一概念。

第6阶段是检查到目前为止已经接受的被反驳的原始猜想的推论。我们能够挽救这些推论吗？或者说引理被反驳将导致巨大的灾难吗？例如，逐项积分是傅里叶猜想的狄利克雷证明的基石。杜布瓦斯－雷蒙德用戏剧化的语言描述了这一情形：三角级数理论被“刺伤了心灵”，它的两个关键定理其“基础已经被从下面截断”，那么

在这一打击之下，整个理论又被推回到狄利克雷甚至是傅里叶之前的状态。

（杜布瓦斯－雷蒙德［1875］，第120页。）这一状况使我们察看“失去的基础”是怎样重新获得的，成为一项激发兴趣的研究。

在这一过程中，大量的反例被发掘出来。但是对它们的研究——方法的第7阶段——只是在19世纪最后几年才开始。（例如，杨（Young）的关于非一致收敛点的分类和分布的工作，杨［1903—1904］。）

【注释】

[1]正如我所强调的，历史的实际模式也许可以稍微偏离这一探试的模式。第4阶段有时也可以在第3阶段之前（甚至在探试法的顺序中）——一个精巧的证明分析也许可以引发出反例。

[2]编者按：换句话来说，这种方法（某种程度上）是由其产生的一系列陈述P₁，…，P_n组成，以至于P₁＆…＆P_n对于某些引人关注的对象域被认为应该是真的，并且似乎蕴含了原始猜想C。结果可能发现这不是事实——换句话说，我们发现的情况是，其中C为假（“全局的反例”），但是P₁到P_n却成立。这就导致我们要清楚地说明也被这一反例（“局部反例”）所驳倒的一条新的引理P_n＋1。因此，先前的证明就被一个新的证明所替换，新的证明能够被概括为如下的条件陈述：
P₁＆…＆P_n＆P_n＋1→C。
这一条件陈述的（逻辑的）真不再被反例所驳斥（因为既然现在前件为假，那么条件陈述则为真）。

[3]休厄尔（Whewell）［1858］，1，第152页。在1858年时，休厄尔至少已落后10年了。这一原理是源于莱布尼茨的连续性原理（［1687］，第744页）。博耶（Boyer）在其［1939］第256页引用了出自鲁易里［1786］第167页的对这一原理特征的重新表述。

[4]这一《热传导研究报告》获得了1812年的数学大奖，它曾受到拉普拉斯（Laplace）、勒让德和拉格朗日（Lagrange）的评判。（译注：1811年底，傅里叶把他关于热传导的研究报告提交给巴黎科学院，裁决者拉普拉斯、拉格朗日和勒让德严厉地批判了这份报告，以致没能在科学院得到发表，如今它已是一篇这一领域的经典文献了。）这一报告在傅里叶经典的《热理论》1822年出现之后才得以出版，比柯西的教材晚了一年，但是《热理论》的内容那时已经众所周知了。

[5]傅里叶，见前面所引用的书，第177页和第178页。

[6]写下这一句之后，我发现“非连续的”这一术语大致上以柯西的意义出现在一些迄今未出版的泊松（Poisson）［1807］和傅里叶［1809］的手稿中，J·拉维茨（J.Ravetz）博士正在研究这些手稿，他好意地允许我看他的影印照片。这的确给我带来了麻烦，虽然它并没有驳倒我的证据。傅里叶在不同的时候心中显然有两种不同的连续性的观念，而且，这两种不同的观念相当自然地产生于两个不同的领域。如果我们如此解释一个函数：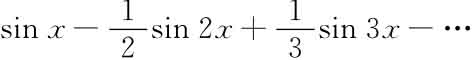

把它当作一条弦的初始位置，它肯定会被认为是连续的，截断垂线——像柯西的定义所要求的那样——看起来是不自然的。但是，如果我们把这一函数解释为，就是说，代表一条金属线上的温度，这一函数显然是非连续性的。这些考虑因素暗示了两个猜想。首先，柯西的著名的连续性定义，它与函数的“弦的解释”相冲突，它也许是受到了傅里叶对热现象的观察的激发。其次，傅里叶对这些非连续函数图中存在的垂线的坚持根据热解释，也许是源于不与莱布尼茨的原则发生冲突的一种努力。＊编者按：关于傅里叶数学的进一步的信息，见I·格拉坦－吉尼斯（I.Grattan－Guinness）（与J·R·拉维茨合著）的《约瑟夫·傅里叶，1768—1830》（麻省理工学院出版社，1972年版）。

[7]那就是上面说的弦的常识或者图示的常识。

[8]编者按：这里什么被侵害了呢，也许不是我们直觉的连续性的观念，而是我们关于任何代表函数的图示轻微旋转后仍然代表某一函数的信念。从直觉的观点看，傅里叶曲线是连续的，这种直觉还可以通过连续性的ε、δ定义（这通常被记在柯西头上）来说明因为傅里叶曲线，包括垂线在内，可以用两个连续的函数来进行参数的表示。

[9]见前面引用的书（指《热传导研究报告》），第177节。当然，这一评论距发现收敛在这些地方是无限缓慢的还很远，只是在计算傅里叶级数有了40年的经验之后，这一点才被发现。在狄利克雷对傅里叶猜想所做的决定性改进，表明只有那些其值在非连续点上是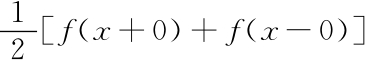的函数才能够被傅里叶级数来表示之前，这一发现是不可能做出来的。

[10]阿贝尔［1826b］，第316页。

[11]柯西［1826］。这一证明是基于不可矫正的错误假设（参见例如黎曼［1868］）。

[12]莫格诺［1840—1841］。

[13]狄利克雷［1829］。

[14]赛德尔［1847］。

[15]这妨碍了柯西给他的老的证明作出一个清晰的批判性评价，并且甚至妨碍他在其［1853］第454—459页中清晰地用公式表述他的定理。

[16]见前文，第20—27页。

[17]阿贝尔［1826］，第316页。

[18]给汉斯丁的信（［1826a］）。信的其余部分也很有趣，反映了阿贝尔的例外排除法：“一个人按照一般的方法行进，这不太难；但是我不得不非常审慎，因为命题一旦没有经过严格的证明（即没有任何证明）而被接受，就会在我心中扎根，以至于我每次都会不加进一步的检查而冒险使用之。”由此，阿贝尔挨个检查了这些普遍的猜想，并试图推测它们的有效性的范围。
这种笛卡儿式的对于绝对清晰的幂级数的自我强加的限制，可以解释阿贝尔为什么特别关心要严格地对待泰勒（Taylor）展开式：“泰勒定理，所有无限小演算的基础并没有很好地确立起来。我仅仅发现了一个严格的证明范例，那就在M·柯西的《无限小演算讲义提纲》中，他在那里证明了，只要级数是收敛的，就会有：
φ（x＋a）＝φ（x）＋aφ′（x）＋a²φ″（x）＋…，
但是，人们却在不加考虑地在所有情况下使用它。”（给霍尔姆博（Holmbo3）的信［1825］。）

[19]阿贝尔［1826b］，卷1，第314页。这一版本是从德文本转译的（原法文本是由克赖莱译为德文的）。＊编者按：看起来阿贝尔好像忘记了α左右两边的模符号（the modulus sign）了。

[20]普林斯汉姆［1916］，第34页。

[21]哈代［1918］，第148页。

[22]布尔巴基［1949］，第65页以及［1960］第228页。

[23]参见前文，第20—27页。

[24]有两位数学家注意到阿贝尔的证明并不是毫无缺陷的。一位就是阿贝尔自己他再次认真地探讨了这一问题——不过没有成功——在其死后出版的论文“论级数”之中（［1881］，第202页）。另外一位是希洛（Sylow），他是阿贝尔选集第二版的编者之一。他为定理加了一个关键的脚注，他在其中指出我们必须在证明中要求一致收敛而不是像阿贝那样的简单收敛。但是他没有使用术语“一致收敛”，对此他好像还不知道（约当的《分析教程》第二版还没有出版），代替这一术语，他引用了杜布瓦斯－雷蒙德（du Bois－Reymond）后来的概括，这只是表明即使他也没有看清缺陷的性质。赖夫（Reiff）在其［1889］中以阿贝尔定理是有效的这一幼稚的主张拒斥了希洛的批评。赖夫说如果柯西是收敛理论的创立者，那么阿贝尔则是级数连续性理论的奠基人：
简要总结柯西和阿贝尔的成就，我们可以说：柯西在其《代数分析》中发现了收敛理论和无限级数的发散性，而阿贝尔在其《论二项式级数》中发现了级数连续性的理论。（［1889］，第178—179页。）
在1889年这样说，的确是一件夸大其词和无知的事了。
不过，阿贝尔定理的有效性当然是由于非常狭隘的零定义，而不是因为证明。阿贝尔的论文后来出版于莱比锡1895年的《奥斯特瓦尔德经典》（第71卷）中。在注释中，希洛的评论未加任何评语地复制在上面。

[25]朱迪安［1912］，2，第527页。

[26]理性主义者怀疑根本没有什么方法论上的发现。他们认为方法是不变的、永恒的。的确，方法论的发现者往往会被恶劣地对待。在他们的方法被接受之前，它会被像不正常的理论一样看待；被接受之后，又会被视作平庸的老生常谈。

[27]赛德尔［1847］，第383页。

[28]“对于方法而言，我已经不得不赋予它们几何学中所要求的全部的严格性，以便永远不依靠从代数学的一般原则中来汲取动力。”（柯西［1821］，导论。）

[29]阿贝尔［1825］，第263页。

[30]“给过于扩大的论断带来有用的限制。”（柯西，［1821］。）

[31]阿贝尔［1825］，第258页。

[32]同时代的人一定认为这一清肃有“一点严厉”。（柯西，［1821］，导论。）

[33]阿贝尔［1825］，第257页。

[34]18世纪的“形式主义”是彻头彻尾的归纳主义。参见第133页，柯西在其［1821前言中拒绝归纳，认为归纳只是“有时适合于展现真理”。

[35]阿贝尔，［1826a］，第263页。对柯西和阿贝尔来说，“严格的”就意味是演绎的与归纳相对立。

[36]柯西［1821］，导论。

[37]编者按：这一段话似乎是错误的，我们毫不怀疑拉卡托斯——他最终还是恢复了对形式演绎逻辑的崇高敬意——他自己也将修改这一段话。一阶逻辑已经达到了推理的有效性的特点描述，（相对于语言的“逻辑”术语的特性来说）它的确使有效的推理本质上是不会出错的。因此，需要被认可的只是拉卡托斯提到的两点中的第一点。通过充分正当的“证明分析”，所有的疑惑可以扔到公理（或者定理的前件）的头上，而不留下任何疑问给证明自身。多证多驳法无论如何不会因为拒绝承认第二点就无效了（如文中所示）：实际上，也许通过这一方法，证明被改进了，以至于所有为了使证明有效不得不做的假设都变得明确了。

[38]就在这10年期间，黑格尔哲学与其绝无谬误论的先辈彻底绝交，并为完全新颖的获得知识的路径提供了一个强有力的出发点。（黑格尔和波普尔代表了近代哲学中独特的难免有错误论者（fallibilist）的传统，但是即使是他们俩也都犯了为数学保留绝对无误的特权的错误。）选自于德·摩尔根（de Morgan）的一段话就表现出20世纪40年代新的难免有错误论者的倾向：
“一种新的倾向时而出现，就是拒绝接受任何有困难的东西，或是如果在检查明显的矛盾方面还有难度，就不对其下结论。如果这一倾向意味着没有什么东西可以被永久地使用和盲目地信任，如果它不是对于所下论断的全部范围都为真的话，那么，至少我不应该对如此理性的方法提出任何反对的。但是，如果其暗示的是凡是不能被全面理解的，就不可以传授给学生，不管有没有加以提醒。要是这样的话，我将反对这种限制，在我看来这不仅会导致错误地看待我们已确知的东西，而且会阻止发现的进程。在几何学之外，下面这一点并不真实，就是许多人认为数学科学在其所有部分其模型是完全精确的。分析的最远的边界还始终没有被完全理解，因为超出边界的区域还是绝对未知的。但是，扩大已定疆土的方法不是留在疆土之内，［这一评论是针对例外排除法而言的］而是要进行航海发现，我非常赞同学生应该接受这样的训练；也就是，既要教他怎样勘察边界，又要教他怎样开垦内陆。因此，在书的后面的部分，我毫不犹豫地使用这些方法，我并不认为它们是令人怀疑的，只是因为这些方法表现为未完成的形式，并且也因为怀疑只是有期望的初学者的怀疑，并非未得到满足的批评家的怀疑。经验时常表明，有缺陷的结论会被坚持不懈的思考修正为可理解和具严格性的，但是，谁可以思考那些从不允许在他面前出现的结论呢？把注意力唯一地放在数学中那些不需要对疑点进行讨论的部分，结果会造成对那些绝对需要通过分析的扩展而前进的模式的厌恶。如果把对数学的较高级的部分的开垦留给专门为此目的而训练的人去做，也许会有些理由不让普通的学生来涉及这些不仅是未确定的部分，而且甚至是抽象科学纯粹推理的部分；把这些部分保留给那些其职业就是使前者清晰、使后者有效用的人。然而，事实上，在这一疆土之上那些注意到数学的困难的人，没有多少为了实现他们的追求而经受住趣味和环境的变故；而且这样的变故的数量还会上升，因为允许所有有能力学习应用数学的高级部分的学生都有机会进入那些分析的部分开垦，关于分析的部分与其说关键在于其目前在科学事务中的运用，不如说关键在于其将来的发展。”（德·摩尔根［1842］，第vii页。）

[39]依照R·B·布雷思韦特（R.B.Braithwaite）的说法，“数学和自然的（unselfconscious，指不是建立在自我意识之上的、绝对客观的——译注）科学方面的善良的天才欧几里得却是科学哲学的——并且实际上也是形而上学的邪恶天才。”（布雷思韦特［1953］，第353页。）然而，这一评论是源于一种静态的逻辑学家的数学观念。