积分直接相关的极限问题

§1.3　与微分、积分直接相关的极限问题

一、微分中的极限问题

设a是一个定数，f是定义于［a，＋∞）上的可导函数，让我们先考虑当x→＋∞时f（x）和f′（x）的极限问题。当然这两个极限可以都不存在，也可能都存在。试问：

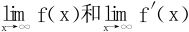之间有什么关系呢？

事实二：。

再请读者朋友思考下列问题：

当时，f（x）是否必是无界函数？

不失一般性，设l>0，∃A，当x>A时，，于是

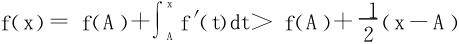
回顾一下渐近线的刻划，若也存在。则y＝f（x）的图形有渐近线y＝ax＋b。

对于或lnx之类，皆有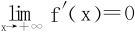，但是并无渐近线，只因上述渐近线存在的后一个条件不满足。不过的存在性之间却有着密切的联系。

例1　若

证　先设l＝0，∀ε>0，∃x₀，当x>x₀时，

当f（x₀）≠0时，令，当x>X时，

一般情形，令g（x）＝f（x）－lx转化即可。

反之如何？即若存在，能否得出也存在呢？显然不行，反例f（x）＝sinx。

退一步思考：已知，且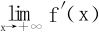存在，则二者一定相等。此结论由例1即可推得。

例2　设φ′（x）连续可导，且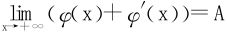，则。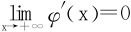

首先说明一下，A＝0和A≠0的情形是两个等价的命题。关键：从形态φ（x）＋φ′（x）入手，联想［e^xφ（x）］′＝e^x（φ（x）＋φ′（x））。

证明　令f（x）＝e^xφ（x），则f′（x）＝e^x［φ（x）＋φ′（x）］。取定一个M，由牛顿莱布尼兹公式有

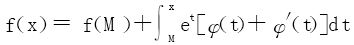
于是

当A>0时，利用洛必达法则（A<0时类似）：

A＝0时，利用上述等价转换命题可得。或者另证如下：

∀ε>0，∃M>0，当x>M时，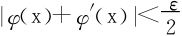

又欲使

故取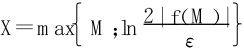，当x>X时，一定有｜φ（x）｜<ε。

浓缩：定性分析是重点，每个题目能给我们一二点启示足矣！

例3　设f在x₀附近有n＋1阶连续导数且f^（n＋1）（x₀）≠0，又

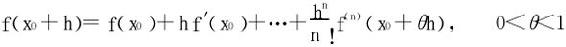
求证。

证明　可将f′（x）在x₀近旁作到n阶Taylor展开：

两个Taylor展开必相等，于是有，

化简为　

左边用Lagrange中值定理：∃0<θ₂<1，使得

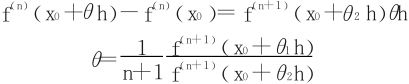
令h→0立得。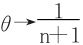

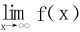例4　设f（x）∈C′［1，∞），且，f（1）＝1，证明存在。

分析　因为f′（x）>0，f（x）单调增加，故只要证明f（x）有上界。

从题给的微分方程要解出f（x）的解析式，无疑有一定困难，故采用放缩技术。

证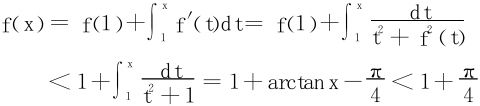　

例5　证明方程xⁿ＋x＝1在（0，1）上存在唯一的根x_n；并且。

可参见§3.4例7。

二、积分式的极限（初步）

积分式的极限题是综合性较高的题目，有多种解题路径，分别介绍如下：

1．洛必达法则

预备公式：变限积分的求导法。如果函数f（x，t）以及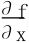都连续，而函数α（x），β（x）都一阶连续可导，则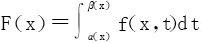关于x可微，且

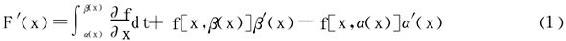
例6　设f（x）连续可微，f（0）＝0，f′（0）＝1，。

解　直接用公式（1）

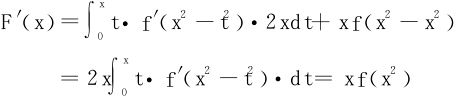
或先将F（x）化为，F′（x）＝xf（x²）。

故

例7　设。

解　n→∞时，转化为求。为了用洛必达法则，须先验证f（x）→∞。

因为

所以。

用洛必达法则：

。

2．放缩法或两边夹

例8　求极限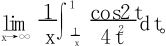

法一　洛必达法则，因为瑕积分发散，故适用型的法则。

法二　因为（利用Taylor展开可知）

所以　　

又

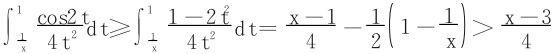
所以

例9　求

解　

得

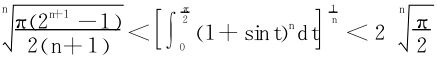
令n→∞得知，所求极限值为2。

下面的例10是例9的推广形式。

例10　设f（x）≥0，g（x）>0，皆为［a，b］上的连续函数，求证：

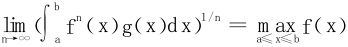
证　设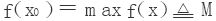，并记于是

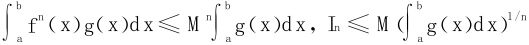
又∀ε>0，∃子区间［α，β］⊂［a，b］，当x∈［α，β］时，f（x）≥M－ε，于是

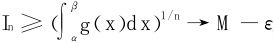。从而原极限得证。

3．换序

定理　若函数列｛f_n（x）｝每一项都在［a，b］连续，且一致收敛，则有

如何判定函数列的一致收敛性？

当连续函数序列｛f_n（x）｝在［a，b］上一致收敛于f（x）时，f（x）也是连续函数。但其逆命题不真，即连续函数序列收敛于连续函数时，此种收敛未必一致。

f_n（x）点态收敛于0但不一致收敛于0。

但加上｛f_n（x）｝对任一x∈［a，b］是单调数列的条件时，f_n（x）就一定一致收敛于f（x），此为Dini定理。

例11　求。

解　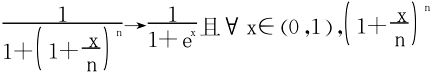是递增的序列，符合Dini定理之条件，故上述收敛是一致收敛，从而

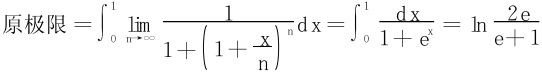
关于极限和积分换序的更深刻的结论，参阅本教材§5.3。下面再罗列一下在勒贝格积分意义之下的换序定理。

勒维定理　设可测集E上的可测函数列满足0≤f₁（x）≤f₂（x）≤…，limf_n（x）＝f（x），则

勒贝格控制收敛定理　设｛f_n（x）｝点态收敛于f（x），且存在可积函数g（x）使在E上几乎处处有｜f_n（x）｜≤g（x），则（3）式亦成立。

若f为［a，b］上的黎曼可积函数，则f一定是［a，b］上的勒贝格可积函数，且极限值相等，故对R-积分的极限问题，不妨视作为L-积分来解决。这样，换序就不要求一致收敛性。如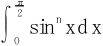，函数列｛sinⁿx｝的极限函数是

读者朋友们，若限定在数学分析的知识范围内，又如何解决上述问题呢？

4．分段技术

例12　求。

故limI _n和是同一个问题的不同形式。

§1.1的例4中已证得后一极限是0，当然也可以反向运用积分的极限来证明乘积式的极限。

解法三　利用分部积分法易求得I _n的递推关系式

于是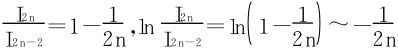　

故发散到－∞，⇔lnI_2n→－∞（部分和首尾相消法），所以I_2n→0^＋，又由于I_2n<I_2n－1<I_2n－2，得I _n→0。

最后，介绍一下著名的Wallis（瓦利斯）公式

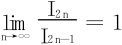对，以及I_2n<I_2n－1<I_2n－2可知：亦成立，将I _n的表达式代入即得。

例13　设f（x）是周期为T的连续函数，求

解　该题不适用洛必达法则，首先分析一下，极限值大概是什么？

特值取代的方法，令x＝nT，n→∞易得

当x≠nT时，设x＝nT＋α（0<α<T）

又

所以有

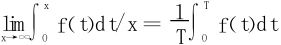
注　特取f（t）＝｜sint｜，得

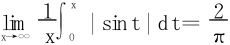
或用放缩法：∀x>0，∃n使得nπ≤x<（n＋1）π

请大家想一想，此法是否具有一般性？

例14　（峰值权函数）设f（x）是［0，＋∞）上的有界连续函数，证明

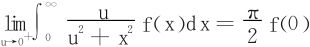
要证的式子等价于

在［0，δ］上，由f（x）在x＝0处的连续性，，

在［δ，＋∞）上，因为f（x）有界，所以∃M>0，使得｜f（x）－f（0）｜≤2M

注　1．峰值权函数类似于概率密度如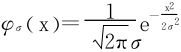，当参数不变化时，其几何图形怎样变化？特征是什么？

　　2．题目中极限的离散化：令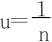，得到

　　3．题中积分上限改为1如何？积分下限改为任意小的数η如何？

习题1.3

1．设f（x）在x＝a附近二阶连续可导，求极限

2．f（x）一阶连续可导，f（0）＝f′（0）＝1，求极限。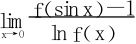

3．设f（x）在［0，∞）上递增有界连续，f″（x）存在且为负，证明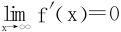（如y＝arctanx）。

4．f∈C²（R），，f″（0）＝4，求极限。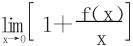

5．设f（x）在x₀附近n阶连续可微，。但是f^（n）（x₀）≠0，且f（x₀＋h）－f（x₀）＝f′（x₀＋θh）h （0<θ<1）。证明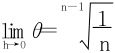。（特取满足题设的多项式函数f（x）＝（x－x₀）ⁿ，易求得。又特取n值，得到一些具体的题目。如n＝3时，f″（x₀）＝0，，）

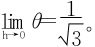6．若f（x）在（0，∞）内可微，且，则∃｛x_n｝→＋∞，使得f′（x_n）→0。

7．求常数a，b，使得。

8．确定常数a，b，使得存在；并求出该极限值。

9．设f（x）∈C［A，B］，且A<a<b<B，证明

10．设a>0，求。

（北师大2007年）

注释

［1］每个y_n都是无理数，但欧拉常数C是不是无理数至今仍不得而知。由此可见，有时证明极限存在和求极限值完全是两码事。