层流的稳定性分析

目前有两种方法可以作为确定层流稳定性的理论判据：一种是能量法，即在一个封闭空间域内，对微弱扰动产生的总能量随时间的变化进行分析。如果扰动能随时间减小，则说明层流是稳定的；如果它随时间增大，则层流是不稳定的。由于这种方法在分析时假定封闭曲面上扰动为零，以致使失稳的雷诺数值估计偏小，所以目前较少采用。另一种方法是小扰动法，即在基本流动中叠加一个与N－S方程相适应的微小扰动，得到扰动方程，然后分析这种扰动量随时间的变化。如果扰动量随时间衰减，则层流是稳定的；如果它不断增长，则是不稳定的，可以过渡到紊流。小扰动法目前广泛使用于平行平面间流动和边界层流动中。最有代表性的理论是瑞利（Rayleigh L，1880）的无黏稳定性理论，奥尔－桑默费尔德（Orr W M F and Sommerfelol A，1907）方程和林家翘（Lin C C，1945）的黏性稳定理论。它们可以用来分析层流运动稳定性的条件以及产生失稳的某些特征，但不能完全显示扰动发展的全过程。由于它们能够比较清楚地表明层流失稳的机制，且与近代的数值计算结果和实验资料的趋势相吻合，因而被人们广泛采纳。

4.2.1 线性稳定性理论的基本方程

由于小扰动法的基本思想是流动中叠加一个适应于N－S方程的微小扰动，所以流场中运动参数可用一个平均流动参数和扰动参数相叠加来表示。在直角坐标系中，设基本流动的速度矢量以U表示，压强以P表示，则相应的N－S方程为

微扰流动的速度矢量以表示，压强以表示。将它叠加于（4－1）式上，有

控制微扰的方程可从（4－2）式与式（4－1）式相减得到。若再略去非线性的微扰项，可得如下的线性化的微扰控制方程

从（4－3）式出发，利用分析其特解而研究稳定性的方法，叫微扰法。有些问题用微扰法得不到解答，因此还有其他研究稳定性问题的方法。

为了便于说明小扰动的基本原则，在这里仅分析二维不可压缩流动，并且假定扰动也是二维条件下的一种最简单情况。严格来说，二维流动中小扰动仍是三维的，但实验表明二维扰动引起的层流失稳比三维扰动时要早，因此不妨以二维来分析。设平均运动参数为Ux＝U（y，微扰场为平面平行场则（4－3）式可以写成

式（4－4）就是小扰动量˜ux、u˜y、p˜的偏微分方程组。虽然它们是从N－S方程中导出的，但与N－S方程不同，它们是线性的偏微分方程组，因而有可能利用分离变量法求解，并具有解的叠加性质。

根据小扰动方程的线性特征，可以将扰动分解为无穷傅立叶分量之和（即把扰动看作由许多离散的部分脉动所构成的，而每个部分脉动看作是沿x方向传播的波）。由于小扰动是二维的，所以由扰动连续性方程可以引入扰动流函数ψ（x，y，t），它与扰动速度分量间的关系为

式中：Ω为微扰场涡量的z向分量。

于是（4－4）式又可写成

式中：V、l为基本流的特征速度和特征长度；φ＝φ（＾y）为仅与＾y有关的某函数；k为波数，为正实数；c一般为复数。

将这些代入（4－5）式中，并经过一定的演算，可得

式中为以特征速度及特征长度表示的雷诺数此式通常称奥尔 －索末菲方程。式的左端为惯性项所产生的，右端是黏性项所引起的。但须注意，这是指惯性和黏性对微扰波的作用，和基本流是有区别的。式中也不显含压强，它的作用只能通过速度变化间接地反映出来。从数学上看，这是一个关于φ的四阶线性常微分方程，一般求解是困难的。

（4－6）式是线性化的微扰法的基本方程。它只适用于基本流是平行直线的流动，是最简单的一类问题。解此方程一般是根据边界条件解得F（Re，k，c）＝0的具体形式。其中c＝cr＋ici。cr为函数c的实部，ci为虚部。由eik（＾x－c＾t）＝e＾x－ci＾t可知因子ekci＾t表示微扰波的振幅随时间的变化，其变化趋向完全由ci控制。若ci＞0，则微扰波的振幅随时间增强，为不稳定；若ci＜0，微扰波的振幅随时间衰减，为稳定；若ci＝0，为临界状态。由此看来，ci是判定稳定性的指标，可以称它为起伏指标；cr则表示微扰波的传播速度。在F＝0中，一般取k、Re为给定的。因此，作为数学问题，就在给定的k、Re及边界条件下，求ci、cr，作为k、Re的函数。即

而重要的是ci＝0时的最小Re（以Remin表示）。 ci＝0称为中性曲线。

解（4－6）式时的边界条件为，即φ′＝0；，即φ＝0；y＝h（或∞）时同上可得φ＝0，φ′＝0。

奥尔 －桑默费尔德方程虽是线性方程，但求解仍然很复杂，所以早期的研究是由瑞利提出的无黏稳定性理论。

4.2.2 无黏稳定性理论及其特征

所有的实验表明，层流失稳时雷诺数值一般是很大的。也就是说，黏性切应力项的作用一般来说是较小的。式（4－6）的左边是由N－S方程的惯性力项推演出来的，右边是由黏性力项导出的。所以瑞利认为，可以在忽略黏性项下来简化小扰动基本方程，并且依此作为分析层流是否失稳的出发点，从而得出层流稳定性理论的一些重要结论。当取a1Re→∞时（即略去黏性项影响），式（4－6）就退化为二阶微分方程

略去黏性项，方程的阶数由四降为二。这样又引起了另外的困难，即理想流体的固壁边界条件只有法向分速与固壁相同，切向可以是任意的，这与事实不符。

从（4－7）式得到的不稳定叫无黏性不稳定。类似地，考虑黏性所得的不稳定，称黏性不稳定。当然这些都是对微扰而言的，基本流仍是黏性的。

瑞利（Rayleigh）最早用（4－7）式研究稳定性问题，因此此式也常叫瑞利方程。瑞利得出一些重要的定性规律，但他未获得临界雷诺数。瑞利的结果如下：

1）速度分布图上出现拐点是不稳定发生的必要条件。

2）中性扰动（即ci＝0）的波速cr小于基本流动的最大速度。

后来托尔明（W.Tollmien）的研究指出：流速分布图上出现拐点是不稳定发生的必要兼充分条件。同时指出，在理想流体中，中性扰动的相速度大于基本流的最小速度，小于基本流的最大速度。

瑞利的两个结论（包括托尔明的推广）在这里不再详加证明。但需指出，它是根据流速分布图来简单地判断稳定性的准则。如流速分布是直线的，无拐点存在，则此流动是稳定的。它也间接地把压强变化与稳定性问题取得联系。如压强沿流减小（即，如收缩段，见图4－6），为加速区，流速分布无拐点，则流动较稳定，不易转变为紊流。若压强沿流增加（即 ，如扩大段，见图4－7），为减速区，有拐点存在，易失稳而转变为紊流。于是稳定性问题与的变化相联系。从第二个准则看，在流速分布为凸形曲线时必存在y＝y0，使＝cr（ci＝0），此层叫临界层。但这里也出现一些问题，如（4－7）式可写成

从而得出：若显然，在y0处有奇点存在。发生这种情况的原因是所根据的（4－7）式为不计黏性的。因此在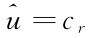的流层，黏性也不能忽略。

图4－6 收缩段流速分布示意图

图4－7 扩大段流速分布示意图

4.2.3 黏性稳定性理论及其特征

由于瑞利的结论在某些流动中未得到验证，而在实际流动中却又发生了层流的失稳，并且过渡到紊流（如圆管内流动），因而引起不少争议，一些人开始怀疑瑞利定理的可靠性。于是，在20世纪初，人们开始考虑黏性对层流不稳定性的影响并作了许多探索。比较系统而成功的研究有林家翘（Lin C C，1955）的稳定性渐近分析理论。

当考虑黏性时计算就变得十分复杂。对速度分布为直线的平行直线流动的计算结果是：微扰的振幅不随时间变化。这意味着此法不能判断流动的稳定性问题。

对速度分布为抛物线型的基本流，例如两固定平行板间由于压强梯度引起的流体运动，经过许多人的努力，最终求得了临界雷诺数及中性曲线。但由于计算十分繁复，我们在这里只给出其轮廓。

应用奥尔 －索末菲方程解本问题时有四个特解φ1、φ2、φ3、φ4，其一般解可以表示成

利用边界条件决定c1、c2、c3、c4与上面相仿。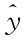＝0时（即下平板面上），φ（0）＝0，φ′（0）＝0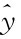；＝y0时（即上平板面上），φ（y0）＝0，p′（y0）＝0。于是可得

因为c1、c2、c3、c4不同时为零，故有特征方程

这是一个包含Re、k、cr、ci的方程。

欲具体讨论基本流的稳定性问题及中性曲线，就必须从此方程解出cr＝cr（Re，k）及ci（Re，k）的显式表示。这就要求先从奥尔 －索末菲方程求出φ1、φ2、φ3、φ4的显式表示，而这在数学上是很困难的，通常用小参量的幂级数表示法。因为要研究的是大雷诺数时的稳定性，可选（k Re）－1／3作为小参量。而在奥尔－索末菲方程的四阶导数的一边。于是产生了如下问题：一方面在零阶近似下方程蜕化为二阶的，只有两个独立解；另一方面在（）＝常数时，前面已知，这时二阶方程有奇点。可是四阶方程在此并非奇点。林家翘注意到了这一情况，并得出解答

式中：Um为基本流的最大速度，h为两板间距之半。所得中性曲线见图4－8所示。

4.2.4 弱非线性理论

图4－8 中性曲线图

弱非线性理论自1960年由Stuart提出以来，已经有40多年了，它不仅被许多人用于流动稳定性问题中，也被用于其他许多学科中，似乎从来没有人对其适用性有过怀疑。但是，随着实验资料的增多，更多的流动细节被提供出来，人们开始发现弱非线性理论给出的结果往往与实验结果不一致。其原因实际上并不难说明。我们如果仔细考察弱非线性理论的解就可以发现，其中实际上只包含了一个实质性的变量，即基本扰动的幅值，其高阶项都是与幅值的幂次成正比例的。而在实际问题中，情况显然不这样简单。特别是实验中若人为引入扰动，其初始扰动形式很难与弱非线性理论给出的解一致。因此，即使最终扰动会趋近于弱非线性理论所给之值（这一点并无保证），但在初始阶段仍不能无条件地应用弱非线性理论。而且在实验或实际问题中，往往转捩在不太长的一段距离内就完成了，究竟弱非线性理论能起多大作用是一个值得考虑的问题。有人在数值模拟中发现，若初始条件由一个T－S波的速度场给定，则平均流的二阶修正项要经历很长时间才能接近于弱非线性理论所给的形式，这在实验室来说，相当于远远超过扰动流经实验段的时间。因此，在应用弱非线性理论时还需多作考虑。对这个问题，周恒在1990年写了一篇短文作了探讨（周恒， 1990）。后来，周恒、尤学一又连续写了两篇文章（周恒，尤学一，1992；Zhou Heng，You Xueyi， 1993），更深入地作了探讨，指出了原弱非线性理论的一些根本性的缺陷，并提出了改进的办法。经改进后的理论，当基本波扰动幅值不太大（例如不大于0.03）时，其结果可以和数值模拟的结果吻合得很好。读者在应用弱非线性理论前，应先阅读这两篇文章，否则，用原弱非线性理论有可能导致错误结论。

4.2.5 非线性理论

如果小扰动是不稳定的，则其幅值将逐渐增长，这时将出现不能用线性理论解释的现象。例如，按小扰动理论，扰动的增长率是指数型的；如果用时间模式，则其幅值将趋于无穷大，这显然与实际不符。再如，扰动幅值增大后，将出现高频（也可能出现更低频的）扰动，而不是单频的。总之，随着扰动幅值的增长，会出现许多复杂的现象，这些都不能用线性理论来说明。这就是非线性理论所研究的内容。

4.2.6 分叉理论（bifurcation）

早在20世纪40年代，L.D.Landau和E.Hoft就分别提出过分叉概念，以希望解决紊流发生的问题。其概念是：当Re很小时，N－S方程的定常解（层流）是唯一稳定的，例如平面Poiseuille流的层流解。当Re逐渐增加而超过某一临界值时，层流解还存在，但已不稳定，这时存在另一个定常或周期性解，而这一解是稳定的。当Re再增加至另一个临界值时，这后一解虽仍存在，但又失去稳定性，而另一种更复杂的准周期解又存在且稳定。如此不断出现新的分叉，流动越来越复杂，终于变成紊流。

这种分叉的概念可以用图4－9（a）来表示，图中纵坐标是解的某种量度，分叉解对应于量度不变的点。但有时，在Re＜Recr时就可以出现分叉，如图4－9（b）。前者称为超临界分叉，后者称为亚临界分叉。图4－9中只画了第一个分叉，虚线代表不稳定解，实线代表稳定解。当然，可能存在的分叉情况不止这两种，详细的分叉理论已超出了本书的范围。

图4－9 分叉示意图

但是应该说明，近年来对混沌问题的研究表明，通过不断分叉而导致运动呈现随机状态（紊流和混沌的关系目前还不太清楚），只是可能的途径之一。而流体力学的实验还不能确切地判明到底哪一种途径是主要的，因为在实验时总不免受到外界扰动的影响，使得经2至3次分叉后的细节带有外界造成的随机性而无法判断。但至少对某些情况，第1、第2次分叉已为实验所证实。

D.D.Joseph在将分叉理论用于解决流体力学问题的过程中做了不少工作（D.D.Joseph， 1976）。分叉理论处理的问题主要有：①找出对应于分叉点的临界参数值；②找出该参数在临界值附近时的分叉解；③判明新分叉解的稳定性。

从本质上讲，分叉理论和弱非线性理论是没有区分的。但是，从原理上讲，分叉理论包含着2次、3次，甚至更高次的分叉，而线性理论则不能处理类似的问题；另一方面，在弱非线性理论中有共振理论，等等，则又是分叉理论不能完全包含的。此外，从数学上讲，弱非线性理论的收敛半径所受限制比分叉理论更大。