薄壁壳体在内压作用下的应力

一、无力矩理论及基本方程

1. 无力矩理论

压力容器的承压结构是壳体，而壳体是两个近距同形曲面围成的结构，两曲面的垂直距离即为壳体的厚度，平分壳体厚度的曲面叫作壳体的中面，壳体的几何形状可由中面形状及壳体厚度确定。

中面为回转曲面的壳体叫作回转壳体，是由两条近距同形曲线绕对称轴旋转360°形成，在垂直于对称轴的截面上的投影是圆环，如圆筒壳、圆锥壳、椭球壳等都是回转壳体。当容器内外表面的距离与壳体的回转直径相比很小时，可以将其看成回转薄壳。设计上一般认为，壁厚与壳体内径之比小于1/10，即外径与内径之比小于或等于1.2（即K≤1.2）的壳体属于回转薄壳。当外径与内径之比大于1.2（即K＞1.2）时，称为厚壁回转壳体。当然，这种区分是相对的，薄壳与厚壳并没有严格的界限。

压力容器中的回转壳体，其几何形状及压力载荷均是轴对称的，相应压力载荷下的应力应变也是轴对称分布的。

为了分析求解回转薄壳中的应力，可以假设壳体是完全弹性的，作为弹性壳体应符合弹性理论的一些基本假设，即材料是连续的、均匀的和各向同性的。此外，对于回转薄壳通常采用以下假设使问题的求解得到进一步简化。

1） 小位移假设

壳体受力以后，各点的位移都远小于壁厚，即为小位移假设。根据这个假设，在考虑变形后的受力平衡状态时，可以用变形前的尺寸代替变形后的尺寸，而变形分析中的高阶微量可以忽略不计，使微分方程简化成线性方程。

2） 直法线假设

壳体在变形前垂直于中间面的直线段，在变形后仍保持为直线，并垂直于变形后的中间面。联系到小位移假设，变形后的法向线段长度保持不变。根据这个假设，壳体沿各点的法向位移均相同，变形前后的壳体厚度保持不变。

3） 不挤压假设

壳体各层纤维在变形前后互不挤压。根据这个假设，壳体法向的应力与壳体截面的其他应力分量相比是可以忽略的微小量，其结果就使薄壁壳体的应力分析简化成为平面应力问题。

以上假设构成了无力矩理论的基础，它可以表述为：当壳体壁厚与直径相比很小时，认为壳体很薄几乎像气球充气后的薄膜一样，其承压后的变形与气球充气时的情况相似，其内力与应力是张力，沿壳体厚度均匀分布，呈双向应力状态，壳壁中没有弯矩及弯曲应力。这种分布与处理回转薄壳的理论叫作无力矩理论或薄壳理论。

无力矩理论简化了壳体的应力分析过程，实践证明，无力矩理论的计算结果可以满足薄壁容器设计的工程精度需要。严格来说，任何回转壳体都是具有一定壁厚的，承压后应力沿壁厚并非均匀分布，壳体中因曲率变化也有一定的弯矩及弯曲应力，当壳体较厚且需精确分析时，应采用厚壁理论即有矩理论。

2. 回转壳体的几何概念

以任意直线或平面曲线作为母线，绕其同平面内的轴线旋转一周即形成旋转曲面。压力容器中的很多承压结构是旋转曲面，如以半圆形曲线作为母线绕其直径旋转一周即形成球面；以某一象限内的椭圆线绕其长轴或短轴旋转一周即形成椭球封头曲面；以直线作为母线绕其同平面内的平行线旋转一周即形成圆柱面；如直线母线与其同平面内的直线相交，则旋转一周后得到的是圆锥面。

薄壁壳体用中间面来表示壳体的几何特性，为了分析问题具有一般性，现以任意形状的母线形成回转壳体，如图6−2所示。OA为旋转轴，形成中间面的平面曲线ADB称为母线，母线绕旋转轴旋转一周形成了旋转壳体。当母线绕旋转轴转到任意位置时，例如，AEC线称为经线，显然经线与母线的形状是完全相同的。经线的位置可以以母线平面为基准，由绕旋转轴的角度θ来确定。经过经线上的任意一点E垂直于中间面的直线称为法线，由几何关系可知，法线的延长线一定与旋转轴OA相交，交点为O2。将法线段EO2绕旋转轴旋转一周，得到一个与旋转壳体正交的圆锥体，圆锥体与旋转壳体的交线为一个圆，如图中的DEF，这个圆称为纬线，纬线的位置可以由中间面的法线与旋转轴的夹角ϕ来确定，即与旋转壳体正交圆锥体的半顶角。

图6−2 回转体的中间面

除了要确定经线和纬线的位置外，在进行壳体应力分析时，还要确定经线和纬线的形状，经线和纬线在某一点的形状用其在该点的曲率半径表示，曲率半径是曲线曲率的倒数，客观上表达了曲线的形状。经线曲率半径（ρϕ）又称为第一曲率半径；纬线曲率半径（ρθ ）又称为第二曲率半径，第二曲率半径等于与旋转壳体正交圆锥的斜高，如图6−3所示。

图6−3 回转壳体中的几何关系

回转壳体承受内压后，其经线和纬线方向都会发生伸长变形，因而在壳体的经向和纬向都存在应力，经向应力用σϕ表示，纬向应力也称为周向应力或环向应力，用σθ表示。

由于轴对称的关系，在同一纬线上各点的经向应力σϕ均相等，纬向应力亦如此。但不同纬线上的经向应力和纬向应力可能是不同的。

3. 薄膜圆筒壳的应力分析

假设圆筒形容器的内径为D，壁厚为δ，在内压p的作用下，筒壁上任意一点将产生两个方向的应力：一是由于内压力作用于封头上而产生的轴向应力（经向应力）σϕ；二是由于内压力作用使圆筒径向均匀膨胀，在圆周的切线方向产生的拉应力（环向应力或周向应力）。由于筒壁较薄，其径向应力 rσ相对于轴向和环向应力要小很多。根据无力矩理论，可忽σθ略弯矩的作用，不考虑弯曲应力，认为σϕ和σθ沿壁厚均匀分布。

1） 经向应力σϕ

用垂直于轴线的A—A截面将筒体截成左右两段，如图6−4所示。左段壳体受力情况（右段与此类似）如图6−5所示。根据力的平衡方程，有：

图6−4 承受内压薄壁圆筒

图6−5 薄壁圆筒轴向应力

2） 环向应力σθ

截取长为L的一段筒体，并用通过轴线的平面将筒体截成两半，保留上半部分，如图6−6所示，建立力学平衡方程，即：

4. 薄膜方程

1） 经向应力σϕ

如图6−7所示，求经向应力时，假想用与旋转壳体正交的锥壳将旋转体截成上下两部分，考虑其中任意一部分在y方向的受力平衡。有两种力影响旋转壳体在y方向的受力平衡，一种是壳体内压力p作用在壳体上并在y方向的投影，由于旋转壳体的轴对称关系，内压力p在垂直y方向的投影合力为0；二是假想移去部分壳体对保留分析壳体的作用力，该作用力沿壳体厚度是均匀分布的，力的方向与假想截面垂直，即壳体的经线方向，用应力表示，记为σϕ，沿y方向列出平衡方程则有：

图6−6 薄壁圆筒环向应力

图6−7 回转壳体的经向应力

式中 p——壳体内压力，Pa；

r——壳体中间面距轴线的垂直距离，mm；

σϕ——经向应力，Pa；

δ——壳体在被圆锥面截开处的厚度，mm；

ϕ——圆锥面的半顶角，（°）；

ρθ——第二曲率半径，即圆锥体母线的长度，mm。

2） 环向应力

在同一经线上的不同点，其环向应力的数值可能是不同的，因此，求解经向应力的截面法在求解环向应力时就无法使用了。下面可以采用材料力学中使用的微元法解决这一问题。如图6−8所示，从壳体中假想截出一个小的微元体，当微元体足够小时，微元体上的环向应力就可以表示该点的环向应力。

微元体由下列三对截面截得：一是壳体的内、外表面；二是两个相邻的包括壳体经线和轴线的经线平面；三是两个相邻且与壳体正交的圆锥面，如图6−8（a）所示。

将微元体用假想的截面截出放大后如图6−8（b）所示，此时，微元体仍然处于平衡状态，即微元体上各分力在法线方向的投影之和等于零。

经分析可知，微元体上的外力共有以下几种：一是作用在壳体表面的压力p在法线方向的投影；二是作用在垂直于经线平面内的应力σθ在法线方向的投影；三是作用在垂直于纬线平面内的应力σϕ在法线方向的投影。

为了分析问题，将微元体分别沿经线方向投影和纬线方向投影，如图6−8（c）所示，沿法线n方向列力的平衡方程如下：

图6−8 回转壳体的应力分析

（a）微元体的截取；（b）微元体的应力；（c）微元体法线方向的受力平衡

式中σϕ——微元体上的经向应力，作用在上、下两个周（纬）向圆锥截面上，Pa；

σθ——微元体上的环向应力，作用在相邻两个经向截面上，Pa；

δ——壳体厚度，mm；

dl1——微元体沿经线的长度，mm；

dl2——微元体沿环向的长度，mm；

dϕ——两圆锥截面的夹角，（°）；

dθ——两经向截面的夹角，（°）。

因dϕ及dθ很小，所以有：

式中 ρϕ——微元体经线曲率半径，第一曲率半径；

ρθ——微元体纬线曲率半径，第二曲率半径。

式（6−3）和式（6−4）是求解薄壁回转壳体在内压作用下应力的基本公式，称为无力矩理论薄膜应力方程组，即：

二、无力矩理论在旋转薄壳中的应用

在介绍求解无力矩理论的基本方程时，回转壳体的母线形状没有作特殊要求，因此，从该理论推导出的薄膜应力方程具有一般适用性，压力容器中常用壳体的母线形状是几种典型的母线特例，下面分别说明。

1. 圆筒体

当一条直线围绕与之平行的轴线旋转一周时，就构成了圆筒体的中间面。因此，圆筒体的母线为一条直线，即经线曲率半径ρϕ=∞；与筒体正交的锥体退化成一个平面，可以理解为锥顶仍然在筒体的轴线上，因此，圆筒体的纬线曲率半径ρθ等于筒体中间面的半径r。将ρϕ和ρθ的值代入薄膜应力方程组（6−5）得：

式（6−6）与式（6−1）和式（6−2）比较，可知完全相同。

在薄壁圆筒壳体中，环向应力及经向应力（轴向应力）与内压、圆筒半径成正比，与壁厚成反比，且环向应力在数值上是经向应力的两倍。

图6−9 圆锥壳的几何关系

2. 圆锥壳

与圆筒体类似，圆锥壳的母线也是一条直线，但该直线与轴线的交角为α，母线绕轴线旋转一周后形成了圆锥壳的中间面，母线与轴线的交角α称为圆锥壳的半顶角，因此，圆锥壳的经线曲率半径ρϕ=∞；与圆锥壳正交的锥体顶点仍然在圆锥壳的轴线上，在圆锥壳设计中，常采用锥壳上某点到轴线的距离r表示锥壳上的位置，这样锥壳和纬线曲率半径ρθ与r的关系如图6−9所示，可以表示为：

将圆锥体的经线曲率半径ρϕ和纬线曲率半径ρθ的值代入薄膜应力方程组（6−5）得：

从方程组（6−8）中可以看出，圆锥壳上不同点的应力是不同的，从锥顶到锥底，应力随r 的增大而增大。锥底的环向应力和经向应力达到最大应力；在圆锥壳任意一点，其环向应力是经向应力的2倍。圆锥壳的半顶角对其应力有显著影响，半顶角越大，圆锥壳体中的应力越大。

3. 球壳

在压力容器中，使用的球形容器包括球形储罐和球形封头，它们的中间面是一条半圆形或四分之一圆线绕半径旋转一周形成的。由球壳的对称关系可知，球壳的经线曲率半径ρϕ和纬线曲率半径ρθ都等于球壳的半径r。

将球壳的经线曲率半径ρϕ和纬线曲率半径ρθ的值代入薄膜应力方程组（6−5）得：

由此可看出，球壳上任意一点的环向应力与经向应力相等，如果球壳与圆筒直径及壁厚相同，且承受同样的内压，则球壳中的最大应力是圆筒中最大应力的二分之一。

4. 椭球壳

椭球壳的母线为一条椭圆线。通过前面的计算可知，要求解椭球壳上的应力必须求出椭球壳的经线曲率半径和纬线曲率半径。由于椭圆线的特点，求解经线曲率半径和纬线曲率半径比求解圆筒体、圆锥壳和球壳时要复杂。

设椭圆的长轴为2a，椭圆的短轴为2b（如图6−10所示），椭圆方程为：

图6−10 椭球壳的几何关系

连续曲线的曲率半径可以通过该曲线的一阶导数和二阶导数求出，如果曲线方程为：y= f (x)，则在曲线上任意一点A的曲率半径为：

由椭圆方程可知：

椭圆上点的曲率半径为：

椭圆壳经线上点的曲率半径为：

由图6−10可知，椭圆壳纬线上点的曲率半径（圆锥面的母线）可由下式求得

由上式可知，x是确定椭球壳位置的变量，要求出ρθ关键是求出tanθ，而θ角是圆锥面的半顶角，即椭球壳上该点的切线与x轴的夹角。tanθ等于曲线在该点的斜率，同时等于曲线在该点的一阶导数：

将ρϕ、ρθ的值代入薄膜方程，即可求得椭球壳上任一点的应力：

以x为变量在图6−10所示的坐标内依次画出椭球壳各点的经向应力和环向应力，因椭球壳是对称于y轴的，所以，可以只画出y轴一侧的应力分布，首先考查椭球壳上两个特殊点的应力值，即椭球壳极点和赤道上的应力值。

椭球壳的极点是椭球壳与坐标轴y的交点，在该点x=0，代入式（6−10）和式（6−11）可得：

所以，σϕσ＝θ。

即在椭球壳的极点上，环向应力与经向应力大小相等，其值与椭球长短轴的比值有关，即与椭球壳的形状有关。椭球长短轴的比值越大，极点处的应力数值也越大。

椭球壳的赤道是椭球壳长轴所在平面与椭球壳相交的交线，在赤道上x a＝ ，将x＝a代入式（6−10）和式（6−11）可得：

当椭球壳与圆筒体相连接时，椭球壳的长半轴a与圆筒体的半径r相等，因此，在连接处椭球壳与圆筒体的经向应力始终相等，与圆筒体的大小和椭球壳的形状无关。

由上式可知，σθ的大小和正负取决于椭球长短半轴的比值：

当时，在椭球壳赤道上环向应力出现负值，即曲线上的环向应力为压缩应力。由此可见，椭球壳上的环向应力和经向应力的大小和方向均受到椭球壳长短半径比a的影响，且a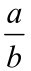越大，即椭球壳深度越小，应力分布越不均匀，但如果深度过大，又为椭球壳的加工制造带来困难，综合考虑椭球壳的受力状态和加工质量两方面的因素，将a =2的椭球封头定义为标准椭球封头，标准椭球封头上的应力分布规律如图6−11所示。

图6−11 标准椭球封头应力分布规律

将标准椭球封头与半径等于其长半轴 a的圆筒壳比较，如果二者有相同的壁厚并承受同样的内压，则封头赤道上的环向应力与圆筒壳上的环向应力大小相等，方向相反；封头赤道上的经向应力与圆筒壳上的经向应力大小相等，方向相同；封头极点处应力（环向及经向）的大小及方向都与圆筒壳上的环向应力相同。因而标准椭球封头可以与同厚度圆筒壳衔接，所得到的容器受力比较均匀。

当椭球封头与圆筒体相连以后，椭球封头的环向应力σθ将有所缓和，在连接处附近，将会出现边缘应力与薄膜应力叠加后改善椭球壳周向压应力过大的状况。

例 6−1 列管式换热器的顶部为半球形封头，中间为圆筒体，底部为标准椭球封头。三部分壳体的平均直径为 500 mm，各部分的壳体厚度均为 8 mm。流经壳程的一次水压力为p1=4.6MPa，流经管程的二次水压力为p2=4MPa。试计算换热器各部分壳体的应力。

解：

1） 半球形封头的应力

根据式（6−9）可知，球形封头中的环向应力和经向应力相等，即：

2） 筒体的应力

根据式（6−6）可知，圆筒体上的环向应力和经向应力分别为：

3） 椭球封头的应力

本换热器采用的是标准椭球封头，可根据图6−11确定椭球封头顶点和赤道上的应力。

顶（极）点上的应力：

赤道上的应力：

5. 承受液体压力的壳体应力分析

承受液体压力的壳体，如内装液体物料储槽，由于液柱静压力，壳体上的各点所受的压力将随深度的不同而变化，同一深度的液压是相等的，液柱越高，液体的静压力就越大。对于承受液体压力的直立圆筒壳体，其器壁上各点所受的静压力可用图 6−12 中的三角形来表示，闭式圆筒形壳体壁上任意点M的压力p按下式计算。

式中 p0——液体表面的压力，Pa；

γ——液体的重度，N/m3；

H——液面的高度，m；

z——筒壁上任意点距底面的高度，m。

若此壳体为底部周边支承的直立圆筒形封闭式壳体，如图6−12所示，设 0p为液体表面上的气压，液体重度为γ，壳体的直径为D，壁厚为δ。因为圆筒形壳体纬线曲率半径ρθ为圆筒形半径；经线为直线，其曲率半径ρϕ为无穷大，所以由式（6−6）即可求得环向应力σθ。

图6−12 盛液体圆筒形壳体

对于底部支承的直立圆筒，由于液柱静压力垂直作用于圆筒侧壁，液体重力由支座承担，由截面法思想可知，筒壁中的轴向应力σϕ（或经向应力）只与液柱表面压力p0有关，即：