矛盾无处不在，在数学中也充满着矛盾。在我们所学习的初等数学内容中，我们可以体会到数与形、有限与无穷、必然与或然、抽象性与多用性之间的矛盾，也有已知与未知、直与曲、常与变、连续与离散等矛盾，数学中处理这些矛盾所体现的思想方法被称为数学辩证思想方法。
这里我们首先以讲解“一元二次不等式的解法”为例。
高一年级第一学期教材上是这样表述的：
一般地，设一元二次不等式为ax2＋bx＋c＞0或ax2＋bx＋c＜0（a＞0），当对应的一元二次方程ax2＋bx＋c＝0的根的判别式Δ＝b2－4ac＞0时，先求出方程ax2＋bx＋c＝0的两个实数根x1，x2（不妨设x1＜x2），于是不等式ax2＋bx＋c＞0的解集为｛x|x＜x1或x＞x2｝；不等式ax2＋bx＋c＜0的解集为｛x|x1＜x＜x2｝。
等式与不等式是矛盾的，但是在一元二次不等式的解法这里实现了统一。
唯物辩证法认为，矛盾是普遍存在的，矛盾是事物内部及事物之间既对立又统一的两个方面，即辩证统一的。对立指矛盾双方相互排斥、相互斗争的关系；统一指矛盾双方相互依存，一方的存在以另一方为前提。相互排斥体现的是斗争的一面，相互依存体现的是统一的一面。
另外，局部与整体是一对矛盾，然而他们又是统一的。让我们来看两个函数的性质——函数的单调性与函数的奇偶性，前者微观，后者宏观。
让我们来回顾一下这两个定义。
函数的单调性：
一般地，对于给定区间I上的函数y＝f（x），
如果对于属于这个区间I的自变量的任意两个值x1，x2，当x1＜x2时，都有f（x1）＜f（x2），那么就说函数y＝f（x）在这个区间上是单调增函数，简称增函数。
如果对于属于这个区间I的自变量的任意两个值x1，x2，当x1＜x2时，都有f（x1）＞f（x2），那么就说函数y＝f（x）在这个区间上是单调减函数，简称减函数。
函数的奇偶性：
一般地，如果对于函数y＝f（x）的定义域D内的任意实数x，都有f（－x）＝f（x），那么就把函数y＝f（x）叫做偶函数。如果对于函数y＝f（x）的定义域D内的任意实数x，都有f（－x）＝－f（x），那么就把函数y＝f（x）叫做奇函数。
函数的单调性是一个微观的性质。考察的是定义域内的某一个区间内函数的单调性，递增还是递减。函数的奇偶性是一个宏观的性质，需要对整个定义域内的函数从整体上来分析。
这样我们既有宏观层面的，又有微观层面的分析，两者统一起来，于是我们就能够更加完整、更加深入地把握该函数了。
再以讲解高二第一学期的“定比分点坐标公式”为例。
已知P是直线P1P2上的点，且
（λ为任意实数，且λ≠－1），P1，P2的坐标分别为（x1，y1），（x2，y2），求点P的坐标（x，y）。
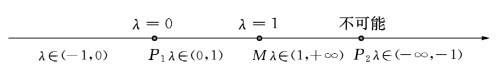
当P在直线左侧无穷远处时，
当P在直线右侧无穷远处时，
这里，由P点位置的变化引起了λ的变化。当P点从P2点的左边向右边逐步跨越的时候，λ却从＋∞一下跳跃到了－∞，这里量变引起了质变。
下面我们再以“点到直线的距离——有向距离”一课为例。
这节课的主要内容是介绍有向距离δ。
已知直线l的方程ax＋by＋c＝0（a2＋b2≠0）以及点P（x0，y0），
定义：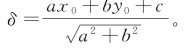
由不失一般性的推导可得结论：
当点P在法向量n→＝（a，b）指向的一侧时，δ＞0；
当点P在法向量n→＝（a，b）指向的另一侧时，δ＜0；
当点P在直线l上时，δ＝0。
因此，δ的符号确定了点P关于直线l的相对位置。
接着我们可以从一般到特殊，给学生呈现这样一个具体例子。
对于直线l：2x＋y－1＝0以及点P（3，3），可求得δP＞0；若将这条直线l的方程改写为：－2x－y＋1＝0，则可得δP＜0。同样的一条直线，同样的一个点，为什么会出现这样两个截然不同的结论呢？通过两个互相矛盾的结论，请学生进行辨析，究竟哪一个正确。
事实是两个结论都正确，因为前者δP＞0，表示点P在法向量n→＝（2，1）指向的一侧，而后者δP＜0，表示点P在法向量n→＝（－2，－1）指向的另一侧，所以两者所描述点P与直线l的相对位置完全一致。
可见，通过看似相矛盾结论的辨析，可使学生的思维更深刻，将概念、定义或定理等领悟得更彻底。这是一个对矛盾的思辨，是一个引领学生体验哲学思辨的例子。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
