习题的变式教学

浅谈数学例题、习题的变式教学

韩苗苗

例题、习题的教学是数学教学的重要组成部分，是把知识、技能、思想和方法联系起来的一条纽带。解数学问题是研究和学习数学的重要途径，通过例题、习题教学，要达到强化双基、传授方法、揭示规律、启发思维、激励创新、培养能力的目的。然而当老师们辛辛苦苦讲练了很多例题、习题后，学生们掌握知识的效果却往往不尽如人意。许多我们认为学生已掌握的知识，在一次次考试中，只要对问题的背景或数量关系稍作演变，就会有许多学生无所适从。这表明:我们在课堂上进行的例题、习题的教学效果不太理想，回想一下，很多时候我们只是就题论题，反复套模式训练，而对例题、习题的教学没有进行深入的思考，处理方法单一，缺乏系统性和变化性，它不仅对学生掌握知识与技能无所裨益，更不能很好的锻炼和培养学生的能力，而且还会使学生逐步丧失学习数学的兴趣。如何提高例题、习题的教学效果呢?我认为例题、习题的变式教学就是一种有效的、重要的教学手段，下面就谈谈我的几点体会:

一、在例题、习题教学中采用变式教学的重要性

在例题、习题教学中，当学生获得某种基本解法后，通过改变题目的条件、题目的结论、改变情境等多种途径，从不同角度、不同层次、不同情形、不同背景做出有效的变化，使其条件或结论的形式或内容发生变化，而本质特征却不变.也就是所谓“万变不离其宗”，以此来强化学生对知识和方法的理解、掌握和变通，帮助他们对问题进行多方向、多角度、多层次的思考，一组由浅入深、富有启发性和探索性的变式题组，不仅能激发学生的兴趣，而且有助于培养和提高学生的发散思维能力，化归、迁移思维能力和思维灵活性。数学教学改革专家顾泠沅创立的青浦四条经验中，其中一条“组织好课堂层次序列，进行变式教学”，就强调了变式训练的重要性.运用变式训练可以提高数学题目的利用率，提高教学有效性，起到综合运用知识，有效培养学生综合思维能力，充分理解数学本质属性的作用.这同时也符合新课程标准的基本理念。

二、变式在例题、习题应用中的主要形式

例题、习题变式主要包括一题多解(证)变式、一题多变变式，多题一解(一法多用)变式和一题多用变式等形式。

(1)所谓一题多解(证)变式，就是对同一个数学问题，引导学生在所学的知识范围内尽可能地提出不同的解题构想和方法，从而达到发散、启迪思维，总结规律、方法，开阔视野，提高分析、解决数学问题能力的目的。一题多解的实质是以不同的论证方式，反映条件和结论的必然本质联系。在教学中教师应积极引导学生从各种途径，用多种方法去思考问题。例如下面这道例题:

已知:如图，AE‖CD，求证:∠A+∠B+∠C=360°。

解一:过点B向右作BF∥AE，利用平行线的性质:两直线平行，同旁内角互补即可证出结论;

解二:过点B向左作HB∥AE，利用平行线的性质:两直线平行，内错角相等，构造出一个周角即可证出结论;

解三:延长AB交CD的延长线于点M，后用三角形一个外角等于与它不相邻的两个内角的和，即可证出结论;

解四:连接AC，利用三角形内角和等于180°和平行线的性质:两直线平行，同旁内角互补即可证出结论;

解五:连接DE，构成五边形，后用五边形内角和进行解答

解六:反向延长AE，CD，再过点B向右作BN∥AE从而三个角构成两个平角。

以上各种证法，沟通了不同知识间的内在联系，达到了深化知识，融会贯通的目的。在代数和几何中这样的例子很多，尤其是几何证明题中，许多证明题都有多种证法。当然，列出各种证法后，教师还应要求学生筛选出最佳方法，这也是多向思维的最终目的。一题多解不仅能强化学生对基础知识的理解和掌握，而且对启迪学生思维，激发学生的学习兴趣也大有裨益。

(2)所谓一题多变变式，就是通过对某一题目进行条件变换、结论探索、逆向思考、图形变化等多角度、多方位的探讨，使一个题变为一类题，达到举一反三、触类旁通的目的，可以培养学生积极思维，触类旁通，提高学生思维敏捷性、灵活性和深刻性。

一题多变是题目结构的变式，变换题目的条件或理论，变换题目的形式，而题目的实质不变，以便从不同角度，不同方面揭示题目的实质，能调动学生随时根据变化了的情况积极思索，寻找解决问题的方法，培养思维的灵活性。

例如:计算:(a+1)(a－1)

解:原式=a2－1

变式1:计算:(a+1)(a－1)(a2+1)

变式2:计算:(a+1)(a－1)(a2+1)(a4+1)

变式3:计算:(a+1)(a－1)(a2+1)(a4+1)…(a2n+1)

由此例题可再变式为以下例题:

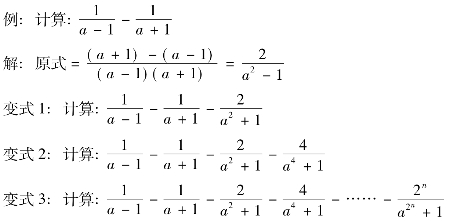
对一个命题的推广有多种途径可循，一般将条件进行相似变换，即在元素的数量上进行推广。几何中常表现为线段或边数(角数)的增加;代数中常表现为变量个数的递增，或常量向变量的转换。命题推广的一个很大特点就是体现思维的发散性和深刻性，这正是培养创造性思维的核心所在。一题多变变式中，图形变式在几何教学中经常遇到，图形变式就是以基本图形为“生长点”，通过将其引申变换为相关图形而得到变式题组，从而培养学生对几何图形的想像能力、变换能力及思维的灵活性和多向性。

(3)多题一解(一法多用)变式:不同单元之间，常常会出现许多内容上的相互转换与渗透，据此，我们可以将某一单元的题目改变表达形式而变为另一单元的题目，但题目本质不变，解答方法相同。另外，通过互为逆否命题转换而得到等价命题，不同题型之间的转换:如选择题转换为填空题，解答题变为证明题、探索开放题等，都属于多题一解的范围。题型变式有助于学生透彻理解题目的本质属性，开阔解题思路，提高解题能力。

(4)一题多用变式，就是以教材中基本例题、习题为目标，探讨该习题及其变通形式的应用，挖掘基本习题的解题功能，从而提高学生解题能力。一题多用的教学设计，实际上是对基本例题、习题教学后的一个反思过程―总结、探索、推广和引申。经常进行这种训练，无疑可以启迪学生思维，培养学生的创新意识，提高其解决问题的能力。

需要说明的是，例题、习题的多种变式形式，不是彼此孤立的，而是相互交叉渗透的，在同一个题目的变式中，常常是各种变式相伴而行。因此，在平时实施的变式教学中，要注意各种变式的交互运用。

三、变式教学要把握好度

数学变式训练不是为了“变式”而变式，而是要根据教学或学习的需要，遵循学生的认知规律而设计，其目的是通过变式训练，使学生在理解知识的基础上，把学到的知识转化为能力，形成技能技巧，完成“应用——理解——形成技能——培养能力”的认知过程。因此，教学中数学变式训练设计要巧，要有一定的艺术性，但也要正确把握变式的度，要有目的性，要起到引导、激发学生思维活动的作用。

1.变式的难度要有“梯度”。变式要循序渐进，要符合学生的认知规律，逐步深入，让学生跳一跳能购得着，否则会使学生产生畏难情绪，反而降低学习的效率。

2.变式教学要提高学生的“参与度”。我们应该提倡让学生参与变式，交流互动，只要学生能够进行变式，教师就不要包办代替，要及时对学生肯定表扬，只有这样，才能调动学生学习的积极性，提高学生参与创新的意识，从而让他们感受到“变式”的乐趣，各种能力也在不知不觉中得到提升。

3.变式的数量要“适度”。变式过多，不但会造成题海，增加无效的劳动和加重学生的负担，而且还会使学生产生逆反心理，对解题产生厌烦情绪。教学效果反而会大打折扣。

实践证明，数学例题、习题的变式教学不仅能使学生全方位、多层次的的认识问题的本质，对学生进行数学技能和思维训练的重要方式，它能有效地培养学生思维的深刻性、广阔性、发散性和灵活性。因此，在数学教学中我们要善于利用变式教学，启迪学生思维，提高课堂教学有效性!